Zadania 3. kola

Koniec: 04. máj 2020 22:00
Do konca: kolo skončilo
"Utečte, temní démoni! Nechajte naše kráľovstvo na pokoji!" "Aha, pozrite, ich domorodý jazyk sa podobá na ten náš, mám pocit, že som počul niečo o temných démonoch" "Nenúťte ma použiť moje zaklínadlá, inak poznáte moc mocnej Sáry!" "Neviete, kedy majú ostatní vyskočiť z tých kríkov?" takto po sebe obe strany konfliktu chvíľu pokrikovali bez toho, aby sa pohli z miesta. Stroskotanci v kríkoch medzi tým v kríkoch aj zostali, keďže sa nedohodli, kedy majú vyskočiť a zaútočiť, tak sa len pozerali, ako Paulus, Lámač a Sára kričia po statočných stroskotancoch pred tanierom. Mali na sebe provizórnu výzbroj a na nej svoj symbol - obrázok ich lietajúceho taniera zvrchu. Po chvíli sa začali nudiť, tak si doň začali vpisovať čísla.

1. príklad

Kategórie:
5
V každom z 8 políčok symbolu je nejaké prirodzené číslo. Každé číslo vo vyfarbenom políčku je súčtom čísel v susedných bielych políčkach. Navyše pre každú dvojicu bielych políčok oproti sebe platí, že ich súčet je 17. Aký je súčet všetkých 8 políčok? Nájdite všetky možnosti.
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Netrvalo dlho a aj 'bojujúcich' začalo unavovať ich neustále zastrašovanie. "Nejedzte nás, sme… sme… dajme tomu, že sme strašní démoni a ak nás obetujete tak… tak vám pokapú všetky žaby a bude pršať dobytok, či tak nejak…" "Dobrý pokus černokňažníci, samozrejme že vás neobetujeme! Každý vie, že to nosí smolu!" Odpovedala im Sára. "Takže to s tou sopkou bol iba blaf! Chytré!" Na to sa Lámač zarazil: "Aká sopka?" "Predsa na naše obetovanie, aká iná?" "Tu naokolo žiadna sopka nie je," povedala im Sára. "Tak prečo ste nás potom pritiahli tým magnetom?" "Čo je to magnet?" začudoval sa Paulus. Nevedel to, pretože jeho mozgové bunky netvorili tie správne spojenia. Keby boli pospájané inak, Paulus by vedel iné veci.

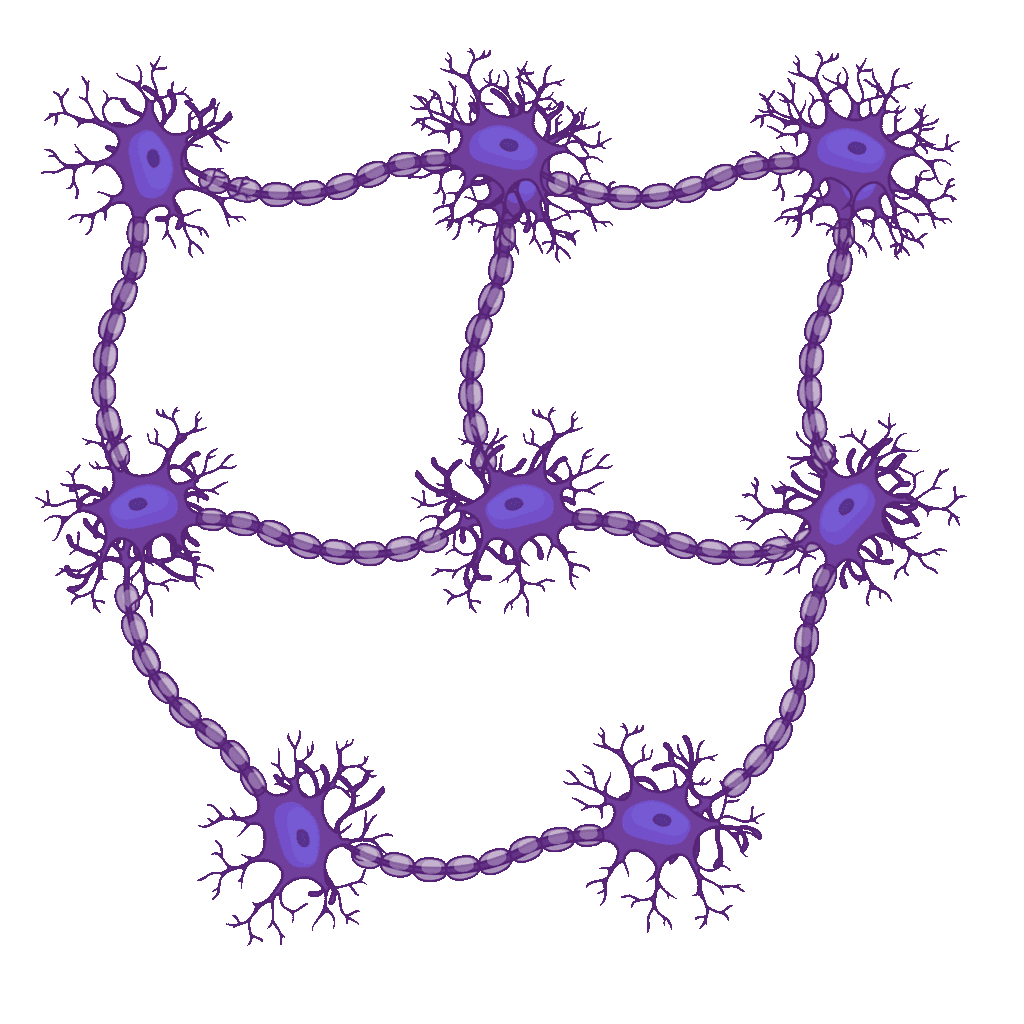
2. príklad

Kategórie:
5
6
Paulus má v jednej časti svojho mozgu osem mozgových buniek. Tieto bunky sú pospájané tak, ako vidno na obrázku. Každá bunka si pamätá jedno písmenko alebo pomlčku. Táto časť mozgu si pamätá názvy tropického ovocia, preto existuje spôsob, akým po spojeniach týchto buniek prejsť tak, aby znaky buniek, ktorými prejdeme, tvorili reťazec ANANAS–KOKOS–MANGO. Nájdite všetky možnosti, ako priradiť jednotlivým bunkám zodpovedajúce znaky.
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
"Nič také nemáme," povedal im Paulus po tom, čo mu stroskotanci, ktorí medzitým vyšli z kríkov vysvetlili, čo je to magnet.
"Ale kto potom pritiahol našu loď?"
"Netušíme, my sme mysleli, že ste na nás prišli zaútočiť"
"To je predsa hlúposť! Odkiaľ to máte?"
"Povedal nám to jasnovidec Jerguš."
"Jerguš? Zaujímavé… Tak sa volá aj náš technik! Keď už o ňom hovoríme, neviete kam zmizol?"
Stroskotanci sa poobzerali, no nikto nepoznal odpoveď. Vtom sa zjavil hologram Jerguša.
"Veľmi dobre, nikdy som o vás nepochyboval. Aj keď je pravda, že prestať po sebe kričať, vám trvalo trošku dlhšie, ako som predpokladal."
"Jerguš!" ozvali sa všetci naraz.
"Áno, presne tak, som to ja. Ale teraz je už na prekvapenia neskoro, všetci vybuchnete. V Paulovom Epickom Meči Sily je totiž bomba!"

3. príklad

Kategórie:
5
6
7
Na displeji bomby je vždy nejaké nezáporné celé číslo. Každú minútu bomba vynásobí všetky cifry tohto čísla a výsledok sa stane novým číslom na displeji. Bomba vybuchne v momente, keď sa na displeji zjaví jednociferné číslo. Napríklad ak je na displeji číslo 732, po jednej minúte bude nahradené číslom 7 \cdot 3 \cdot 2 = 42, a po druhej minúte číslom 4 \cdot 2 = 8, teda po dvoch minútach bomba vybuchne.
  • Nájdite najväčšie nepárne číslo na displeji také, aby malo všetky cifry rôzne a bomba vybuchla už po jednej minúte.
  • Nájdite najväčšie párne číslo na displeji také, aby malo všetky cifry nenulové a rôzne a bomba vybuchla už po jednej minúte.
  • Nájdite najmenšie prirodzené číslo na displeji také, aby bomba vybuchla po troch minútach.
Vzorové riešenie Odovzdať

Komentáre (2)

  • Viki
    28. apríl 2020 13:43

    Dobrý deň, mám dve otázky:

    1. Vybuchne bomba aj ak sa na displeji zjaví iba 0?
    2. Je limitovaný počet cifier na displeji?

    Vopred ďakujem.

  • mišo Vedúci
    28. apríl 2020 15:41

    Ahoj,
    nakoľko aj nula je jednociferné číslo, tak keď sa na displeji objaví, bomba vybuchne. Počet cifier na displeji nie je nijak obmedzený.

    Mišo

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Medzitým sa Šálka snažil utiecť z kráľovskej hladomorne. Teda, nie práve teraz, teraz sa naňho totiž Kráľ prišiel pozrieť. "Ja netuším, kde to som, neviem vám nič povedať!" "To ťažko, temný čarodejný kňažník! Tvoje klamstvá ma neoklamú. Kým mi nepovieš váš plán, nedostaneš žiadne jedlo". Nie že by Šálkovi hrozil hlad, mal totiž stále so sebou termosku s gulášom, ktorú mu stráže dovolili si nechať, keďže ich mozgové bunky nevedeli, čo je to termoska. Momentálne sa Šálka snažil študovať umenie útekov, a tak trénoval mravce, aby utiekli z povrchu hracích kociek.

4. príklad

Kategórie:
5
6
7
8
Šálka položil mravca na hraciu kocku, ktorá má tvar štvorstenu. Kocka má na stenách čísla 1, 2, 3 a 4. Mravec začínal na jednej zo stien a potom osemkrát prešiel na nejakú stenu inú ako tú, kde bol teraz. Dokopy teda prešiel po deviatich stenách. Šálka si zakaždým zapísal číslo steny, na ktorej mravec bol, teda si celkovo zapísal postupnosť deviatich čísel. Na konci bol súčet čísel 30, pričom práve päť z nich boli štvorky. Koľko je rôznych postupností čísel, ktoré si Šálka mohol zapísať?
Vzorové riešenie Odovzdať

Komentáre (4)

  • MatejBachnicek
    14. apríl 2020 19:06

    Dobrý deň,
    zaujíma nás, v akom poradí sú zapísané čísla?
    Vopred ďakujem.

  • mišo Vedúci
    14. apríl 2020 20:40

    Ahoj,
    postupnosti čísel sú rôzne, ak sa líšia čísla na niektorej pozícii. Ak sú teda čísla v inom poradí, aj postupnosti sú rôzne.

    Mišo

  • JúliaPleschová
    26. apríl 2020 15:17

    Dobrý deň,
    na tú stenu kde mravec začínal sa už nevrátil? Teda tam kde začínal bol iba raz?

  • mišo Vedúci
    26. apríl 2020 17:00

    Ahoj,
    mravec mohol na pôvodnú stenu, ako aj ostatné steny, prísť aj viackrát, nemohol však byť dvakrát po sebe na rovnakej stene.

    Mišo

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Teraz je asi načase vysvetliť, čo robil Šálka v kráľovskom paláci. Po tom, čo sa postavil na plošinku, ktorá v skutočnosti bola teleportom, sa objavil v spálni jasnovidca Jerguša. Ten na neho zavolal stráže a tí ho zavreli do hladomorne. Teraz sa Šálka snažil utiecť a zistiť, prečo je Jerguš aj technikom aj jasnovidcom zároveň a prečo sa tvári, že stroskotanci sú nebezpeční. Po mnohých experimentoch s mravcami, ale celou otriasol veľký výbuch. Časť stropu na druhej strane cely sa zrútila, a keďže to vyzeralo, že sa ide zrútiť aj tá druhá, Šálka nemal na výber a rozhodol sa utiecť. Chodba ale nebola úplne rovná.

5. príklad

Kategórie:
5
6
7
8
9
Chodba z hladomorne na slobodu ide najprv rovno, potom hore schodmi a nakoniec dole schodmi. Šálka ide rovnou chodbou rýchlosťou 4m/s, hore schodmi rýchlosťou 2m/s a dole schodmi vie zoskočiť rýchlosťou 5m/s. Na slobodu sa dostal za 56 sekúnd. Potom si však spomenul, že si v hladomorni zabudol termosku s gulášom. Rozhodol sa po ňu vrátiť naspäť do hladomorne, čo mu trvalo 47 sekúnd. Ak rovný úsek chodby má 80 metrov, aká je dĺžka oboch častí schodiska?
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Keď sa opäť dostal na slobodu, zistil, že sa nachádza v trónnej sále, kde si Kráľ s niekoľkými služobníkmi prehliadal miesto výbuchu. "Veľmi zaujímavé, po okolí sú kúsky Epického Meča Sily! Vyzerá to, akoby vybuchol" "Ale ako je to možné? Epické Meče Sily by nemali len tak vybuchovať," vtom si ale Kráľ všimol Šálku. "To si bol určite ty! Spravil si to, aby si mohol utiecť. Stráže, chyťte ho!" Všetky stráže naokolo ale boli zamestnané zbieraním kúskov Meča.

6. príklad

Kategórie:
5
6
7
8
9
Kúskov Meča je neobmedzene veľa a sú očíslované od jedna po nekonečno. Strážkyňa Karin si na papier napíše prirodzené číslo a potom pozbiera toľko kúskov Meča, pričom ich čísla sú posebeidúce. Aké všetky čísla mohla na papier Karin napísať, aby súčet čísel kúskov, ktoré pozbierala, bol vždy násobkom čísla na papieri, bez ohľadu na to, ktoré kúsky vyberie? A čo za číslo tam zase mohla napísať, aby naopak súčet násobkom čísla na papieri nikdy nebol?
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Medzitým sa stroskotanci a hrdinovia pozerali, ako sa Jergušov hologram zatriasol, spadol na zem a vypol sa. "Ach, teraz som si spomenul, že som si môj meč zabudol doma" uvedomil si Paulus. "Som to ale hlupák, našťastie nás to tentokrát zachránilo." "Prečo by to ale Jerguš robil? Musíme ho zastaviť!" "Netušíme ale, kde je." "Pán Kráľ Michal VII nám určite pomôže, musíme sa vrátiť do paláca!" povedal Paulus. "Ale to je veľmi ďaleko, bude nám to trvať prinajlepšom niekoľko dní." "Myslím, že v tanieri máme nejaké zakrivovače priestoru - pokiaľ viete, kam presne musíme ísť, môžeme sa tam dostať rýchlo," vysvetlil Maťko.

7. príklad

Kategórie:
5
6
7
8
9
V rovine máme dané dve navzájom kolmé priamky p a q a bod K - kráľovský palác, ktorý leží mimo týchto dvoch priamok. Zostrojte trojuholník taký, aby p a q boli osi dvoch jeho strán a K jeho ťažisko.
Hneď ako našli správnu trasu ako sa pohybovať, vydali sa do paláca.
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Potom, čo prešli zakriveným priestorom do trónnej sály, stretli stráže, ktoré teraz ešte stále počítali kúsky meča. Po chvíli okolo prebehol Kráľ Michal VII. Keď si ich všimol, podišiel ku nim.
"Vitaj späť Rytier Paulus, vidím, že si si našiel veľkú družinu. Určite odo mňa niečo potrebujete, ale nemôžem vám pomôcť, pretože naháňam temnodejného čarníka. Pokiaľ bude bežať okolo vás, nedovoľte mu prejsť!"
"Ale Pane, prišli sme na to, že žiadni neexistujú!"
"Vážne? Ale koho to potom naháňam?"
"Na tom teraz nezáleží, kde je Jerguš?"
"Naposledy, keď som ho videla, bežal do najvyššej veže," pridala sa ku konverzácií Karin, "tá je ale väčšinou zamknutá"

8. príklad

Kategórie:
5
6
7
8
9
Dvere do najvyššej veže majú 47 zamknutých zámkov v rade za sebou. Na týchto dverách sú aj kľučky. Každá kľučka môže byť stlačená, čím zmení stav dvoch zámkov, na ktoré je napojená, zo zamknutých na odomknuté a naopak. Každá kľučka je napojená na práve dva susedné zámky a každý zámok je napojený na aspoň jednu kľučku. Nájdite aspoň jedno také ponapájanie pri ktorom sa nedá otvoriť viac ako 32 zámkov. Dalo by sa také nájsť aj pre 31? Ak áno, nájdite aspoň jedno a ak nie, zdôvodnite prečo také nie je.
Keď konečne zistili, koľko zámkov bude teba rozbiť, okamžite sa tam rozbehli.
Vzorové riešenie Odovzdať

Komentáre (0)

  • Žiadne komentáre

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Keď hrdinovia vyšli na vrch veže, Jerguš už na nich čakal. "Ale, ale, ale, koho to tu máme, možno ste mi pokazili môj pôvodný plán, vyvolať vojnu aby moja spoločnosť predala viac tovaru, no nebojte sa! Keď sa mi to nepodarilo, aspoň túto planétu vyťažím mojim orbitálnym vrtákom." Potom sa zasmial a stlačil tlačítko na zapnutie vrtáku, ktorý z vesmíru planétu rozbije. Má táto situácia nejaké riešenie?

9. príklad

Kategórie:
5
6
7
8
9

\displaystyle \_ x + \_y + \_z=0 \\ \_ x + \_y + \_z=0 \\ \_ x + \_y + \_z=0

Situácia našich hrdinov je vlastne sústava troch rovníc. Začínajú hrdinovia a následne sa s Jergušom striedajú v ťahoch. V každom ťahu môže niekto doplniť na jedno prázdne miesto v sústave ľubovoľné reálne číslo. Dokážte, že hrdinovia vedia zaručiť, že na konci bude mať ich situácia nenulové riešenie.
"Ako sa opovažujete! Nemôžete vašu situáciu takto ľahko vyriešiť! Na to sa ešte pozrú moji právnici!" zakričal Jerguš a odteleportoval sa preč. "Asi by sme si mali opraviť tanier a pokúsiť sa ho dohnať, nech z toho nemáme problémy," navrhol Viktor. Vtom sa pred nimi opäť objavil Jerguš a zatváril sa prekvapene. Opäť zmizol ale vzápätí sa znovu objavil. "Čo sa to deje?" začudoval sa. Zrazu sa v miestnosti objavil holografický Šálka a povedal: "Išiel som do tvojej spálne a poprepájal som ti teleporty, teraz sa už preč nedostaneš!".
Vzorové riešenie Odovzdať

Komentáre (3)

  • simonkuk
    01. máj 2020 11:29

    co znamena nenulove riesenie?

  • mišo Vedúci
    01. máj 2020 22:23

    Ahoj,
    nenulové riešenie je také, v ktorom aspoň jedna z neznámych x, y, z vyjde iné číslo ako 0.

    Mišo

  • simonkuk
    03. máj 2020 14:56

    k

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa
Keď Jerguša zatvorili do jednej z neporušených ciel v hladomorni, ostávalo im už len vrátiť sa do vesmíru a možno stihnúť koniec vyhodnotenia Intergalaktickej Matematickej Olympiády. Jergušova loď bola plne funkčná, no fungovala pomerne zvláštnym spôsobom.

Prémia 1

Kategórie:
5
6
7
8
9
Tento príklad je iný ako ostatné. Nemusíš spisovať svoj postup, stačí nám poslať riešenie. Viac informácií nájdeš v pravidlách.

Loď vie používať 9 rôznych druhov pohonu. Na začiatku letu si musíme zvoliť, ktorý z nich bude loď používať tak, aby sme vedeli precestovať každý svetelný rok z päťdesiatich, ktoré cestu tvoria.

Pomocou zátvoriek a nasledujúcich operácií: sčítanie, odčítanie, násobenie, delenie, umocňovanie, odmocňovanie a faktoriál; vytvorte 50 výrazov, ktorých výsledkami budú všetky čísla od 1 do 50 vrátane. Použiť môžete len jednu, vami zvolenú, nenulovú cifru. Túto a len túto cifru musíte použiť v každom výraze. Koľko najmenej krát dokopy ju treba použiť?

Umocňovanie je operácia, pri ktorej počítame nejaké číslo (základ) na iné číslo (exponent), na príklad 2^3. Výsledok dostaneme tak, že základ vynásobíme samým sebou toľkokrát, koľko hovorí exponent. V tomto prípade 2 \cdot 2 \cdot 2 = 8.
Odmocňovanie je operácia opačná umocňovaniu. Napr. \sqrt[3]{8} = 2. Pri druhej odmocnine (\sqrt[2]{}) dvojku nepíšeme.
Faktoriál nejakého čísla značíme výkričníkom, napr. 4!. Výsledok dostaneme tak, že zadané číslo postupne vynásobíme všetkými menšími až po 1. V tomto prípade 4 \cdot 3 \cdot 2 \cdot 1 = 24.

Naši hrdinovia ale prekonali aj poslednú skúšku a úspešne sa dostavili na miesto vyhodnotenia. Len čo sa ale ku planéte priblížili, na obrazovke sa objavil robot. STOJTE, CESTOVATELIA Povedal. TÁTO GALAXIA BOLA VČERA OVLÁDNUTÁ ROBOTICKÝM IMPÉRIOM. OPUSTITE NAŠE ÚZEMIE!

Posádka lode sa na seba len pozrela a všetkým došlo, že koniec ich príbehu je ešte ďaleko.

Vzorové riešenie Odovzdať

Komentáre (6)

  • Majko
    25. apríl 2020 17:10

    Použitie iba jednej cifry sa vzťahuje aj na exponenty a n - tú odmocninu?

  • mišo Vedúci
    25. apríl 2020 19:23

    Ahoj,
    je to tak, ako píšeš. Využitie jedinej cifry sa vzťahuje na všetky vpisované čísla, vrátane exponentov a odmocnín.

    Mišo

  • Majko
    25. apríl 2020 20:29

    A vzťahuje sa to aj na druhú odmocninu?

  • mišo Vedúci
    25. apríl 2020 21:25

    Ahoj,
    pri druhej odmocnine sa číslo nepíše, takže sa môže použiť aj s inou cifrou.

    Mišo

  • MatejBachnicek
    01. máj 2020 09:47

    Môžem používať dvojciferné čísla, ktoré majú obe cifry rovnaké (napríklad 33) ?

  • mišo Vedúci
    01. máj 2020 22:11

    Ahoj,
    je možné použiť aj viacciferné čísla, pokiaľ použiješ len jednu cifru.

    Mišo

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa