Riešky tábor - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×10. príklad - Vzorové riešenie
Zadanie
Vyklopené okienko a okno tvoria pravouhlý trojuholník. Nech body Q,R,S sú stredy strán tohto trojuholníka. Okno je v poriadku ak päta výšky P na preponu leží na kružnici opísanej Q,R,S. Dokážte že takéto okno sa nedá pokaziť (bude vždy v poriadku).
Vzorové riešenie
Označme si vrcholy trojuholníku A, B a C, ako na obrázku:
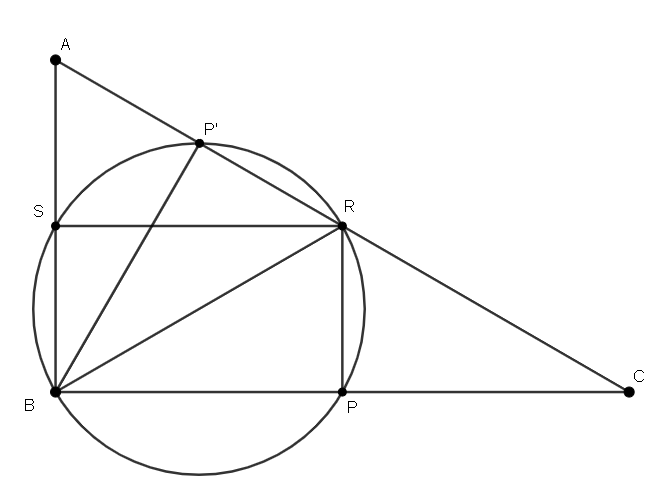
Vyznačili sme aj možného kandidáta na bod P - priesečník opísanej kružnice s priamkou AC, iný ako R. Označme ho P'. V tomto dôkaze sa pokúsime ukázať, že spojnica BP je kolmá na AC - teda je to výška, a P', ležiaci na opísanej kružnici SRQ, je naozaj pätou výšky P.
Poďme to teda ukázať! Vieme, že SR je stredná priečka trojuholníka ABC. Teda bude rovnobežná s jeho stranou, konkrétne BC. Keďže AB je kolmá na BC (lebo sme v pravouhlom trojuholníku), bude SR kolmá na AB.
Rovnako PR je stredná priečka rovnobežná s AB, teda bude kolmá na BC.
To znamená, že v štvoruholníku BPRS sú tri uhly pravé, teda je to obdĺžnik. Obdĺžnik má vždy opísanú kružnicu, a teda toto bude kružnica prechádzajúca P, R a S. Zároveň vieme, že v obdĺžniku leží stred opísanej kružnice v strede uhlopriečky, teda úsečka BR je priemerom tejto kružnice.
Keď vieme, že BR je priemerom kružnice, na ktorej leží P', tak Tálesova veta nám hovorí, že uhol BP'R bude pravý. Teda BP' je kolmá na P'R. Ale P'R je súčasťou AC, teda BP' bude výška na AC. Takže P' bude jej päta. To znamená, že naozaj, P' je P, a teda P leží na kružnici opísanej QRS. Čo bolo treba dokázať.