Riešky tábor - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×4. príklad - Vzorové riešenie
Zadanie
Alain chcel raz vyliezť na budovu, ktorá mala tvar kvádra 40m \times 50m \times 60m. Začínal v jednom rohu a chcel sa dostať do protiľahlého. Liezol tak, že vždy prešiel po celej hrane kvádra na jej druhý koniec. Aby bola jeho cesta zaujímavá, chcel by po každej hrane prejsť najviac raz, ale zároveň by chcel, aby bola cesta čo najdlhšia. Nájdite najdlhšiu takúto cestu a vysvetlite, prečo už nemôže byť dlhšia.
Poznámka: Alain vie liezť po všetkých hranách budovy, teda aj po tých, ktoré sa dotýkajú zeme.Vzorové riešenie
Prvé pozorovanie, ktoré môžeme spraviť je, že keď prechádzame ľubovoľný útvar jedným ťahom, tak ak v danom vrchole nezačíname, ani nekončíme, vždy keď doň prídeme, musíme z neho odísť, takže prejdeme párny počet hrán z neho vychádzajúcich. Pri vrchole v ktorom začíname a pri vrchole v ktorom končíme prejdeme zas nepárny počet hrán, argument je podobný, len prvá, poprípade posledná cesta nemá dvojicu. Toto pozorovanie sa často veľmi hodí. V tomto príklade nám síce mohlo kúsok pomôcť, ale dá sa elegantne vyriešiť aj bez neho. Ešte dodajme, že keď danú myšlienku rozvinieme vieme zistiť, že prejdeme maximálne 9 z hrán nášho kvádrika.
Alain sa chcel dostať z jedného rohu budovy do protiľahlého. Nazvime ich A a F a označme ich oranžovou farbou. Ďalej môžeme predpokladať, že Alain začína v bode A (vieme kvádrik otočiť tak aby začínal v bode A). Všimnime si, že bod A je na spodnej a bod F je na hornej stene kvádra. Vždy keď Alain prelezie po modrej hrane, tak tým zmení či sa nachádza na spodnej alebo hornej stene kvádra. Takže Alain môže prejsť maximálne 3 z modrých hrán o dĺžke 60m, lebo ak prelezie párny počet hrán tak sa vráti späť na spodnú hranu.
Podobne bod A sa nachádza na prednej stene a bod F na zadnej, takže Alain môže preliezť maximálne 3 zo zelených hrán o dĺžke 40m. Nakoniec bod A sa nachádza na ľavej stene a bod F pravej stene. Červené steny o dĺžke 50 m, Alain tiež prelezie maximálne 3.
Dokopy dostávame, že väčšiu vzdialenosť, ako 3\cdot40 \text{m} + 3\cdot 50\text{m} + 3\cdot 60\text{m} = 450 \text{m} Alain určite neprelezie.
Na druhú stranu danú vzdialenosť vie preliezť napríklad ako na nasledujúcom obrázku. Číslo hovorí ako ktorý v poradí bude daný vrchol Alainom navštívený.
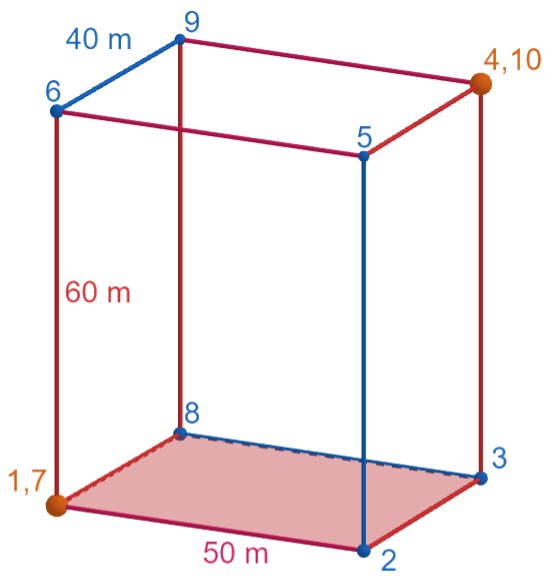
Odpoveď: Najdlhšia trasa, ktorú Alain môže prejsť mala 450\text{m}.