Letný tábor 2025 - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×10. príklad - Vzorové riešenie
Zadanie
Majme obdĺžnik ABCD, zostrojíme body E a F mimo obdĺžnika tak, aby BCE a CDF boli rovnostranné trojuholníky. Priesečník priamky FC s BE označíme X. Kružnica opísaná FBX pretne kružnicu opísanú CDF v bode Y rôznom od F. Priesečník BY s kružnicou opísanou CDF rôzny od Y označíme Z. Keď Z preklopíme osovou súmernosťou cez stranu CD, dostaneme Z’. Dokážte, že Z’ je stred kružnice opísanej CDF.
Vzorové riešenie
Pri geometrii nie je iná cesta, ako si na začiatok nakresliť obrázok. V riešení budeme používať niekoľko vedomostí. Najprv, súčet uhlov v trojuholníku je 180\degreea jednoduché dôsledky, ako napríklad to, že rovnostranný trojuholník má všetky uhly veľké 60\degree. Na druhej strane v tomto príklade budeme veľa pracovať s Tálesovou vetou. Tá hovorí, že pokiaľ máme na kružnici body A,B,C, tak úsečka AC tvorí jej priemer práve vtedy keď \lvert\angle ABC \rvert= 90\degree. Pokiaľ si sa ňou ešte nestretol/la, tak predtým ako budeš pokračovať ti odporúčam si prečítať Wikipédiu. Nakoniec budeme potrebovať zhodné trojuholníky.
Riešenie rozdelíme do niekoľkých fází. Prvým krokom je ukázať, že uhol \angle BXC je pravý. Postupne si všimnime, že \lvert\angle DCF\rvert=\lvert\angle CBE\rvert = 60\degree, keďže sú to uhly pri vrcholoch rovnostranných trojuholníkov. Ďalej ako uhol pri vrchole obdĺžnika \rvert \angle DCB \rvert=90\degree. Teraz ľahko dopočítame uhly \lvert \angle BCX\rvert=180\degree-90\degree-60\degree=30\degree a uhol \lvert\angle BXC\rvert=180\degree-30\degree-60\degree=90\degree.
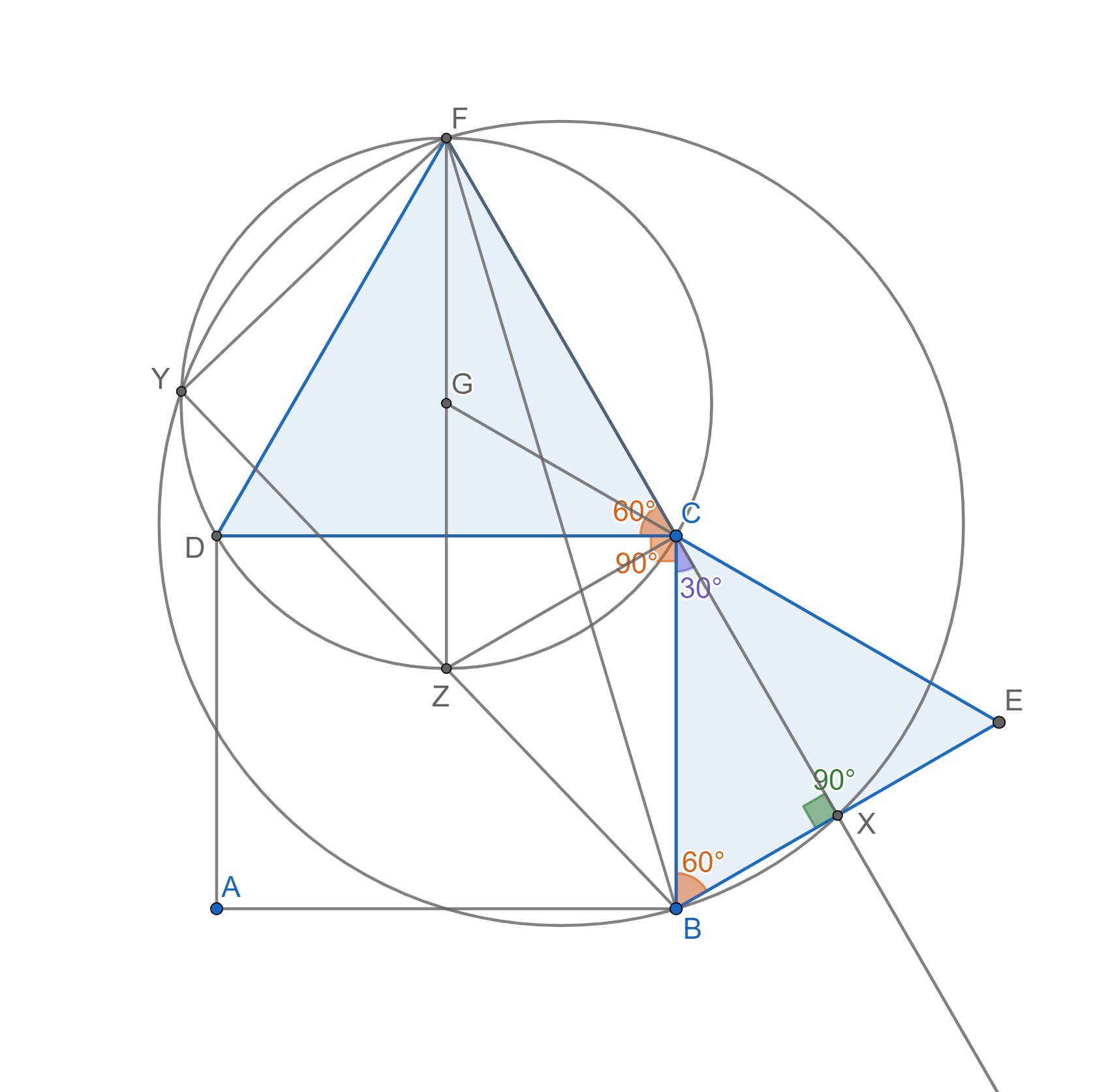
Teraz je čas použiť Tálesovu vetu. Keďže \angle BXF je pravý, tak úsečka BF tvorí priemer kružnice k_1. Potom znovu vďaka Tálesovej vete je aj uhol \angle FYB pravý.
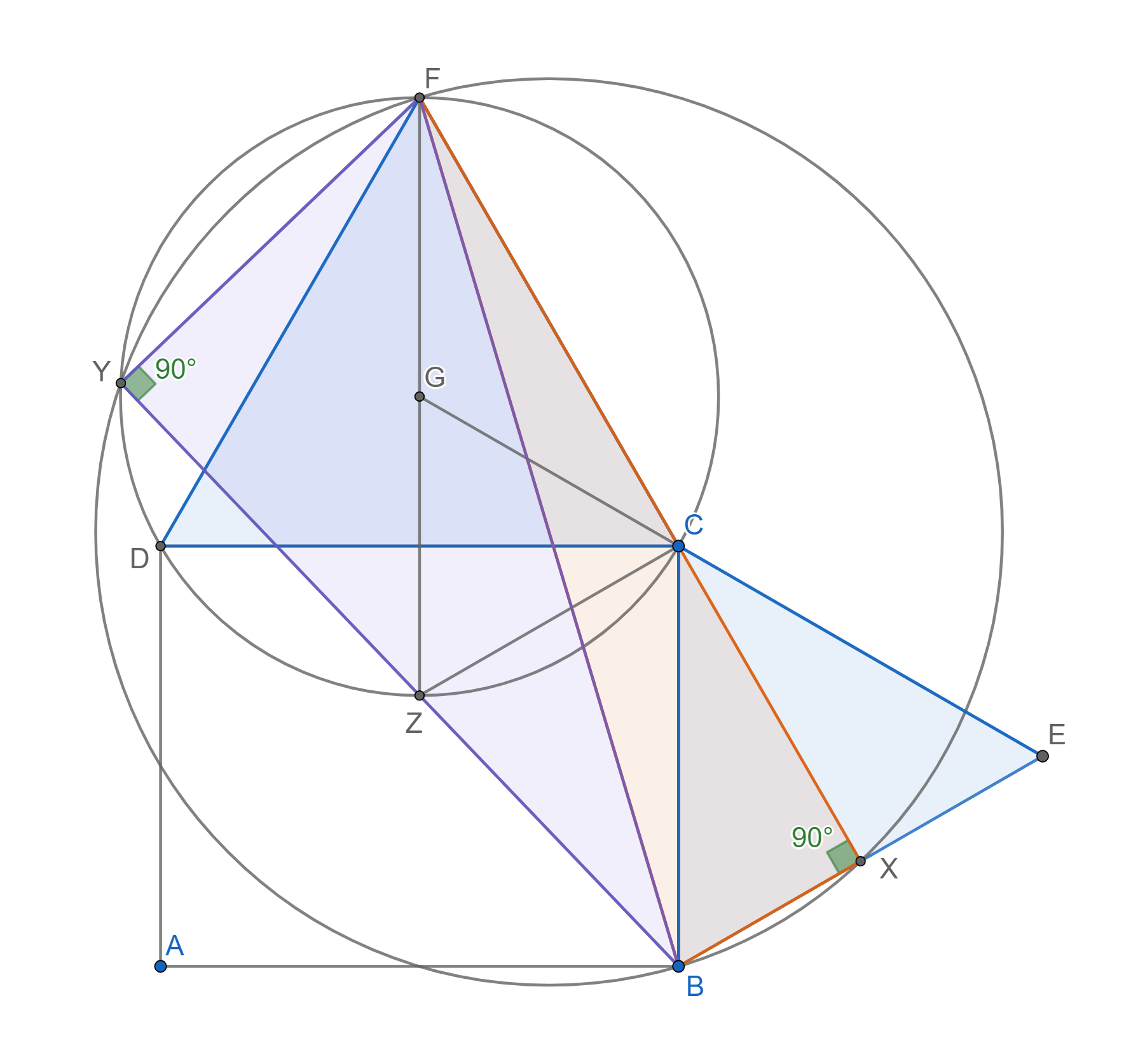
Teraz si všimnime, že body Y, Z a F ležia na kružnici opísanej trojuholníku \triangle DCF a navyše pri vrchole Y máme pravý uhol. Zas použijeme Tálesovu vetu aby sme dostali, že FZ je priemerom kružnice k_2. Ako priemer špeciálne teda prechádza cez jej stred označený ako G. Avšak v rovnostrannom trojuholníku sa stred kružnice opísanej zhoduje s priesečníkom výšok. Špecálne je teda polpriamka \overrightarrow{FG} kolmá na DC.
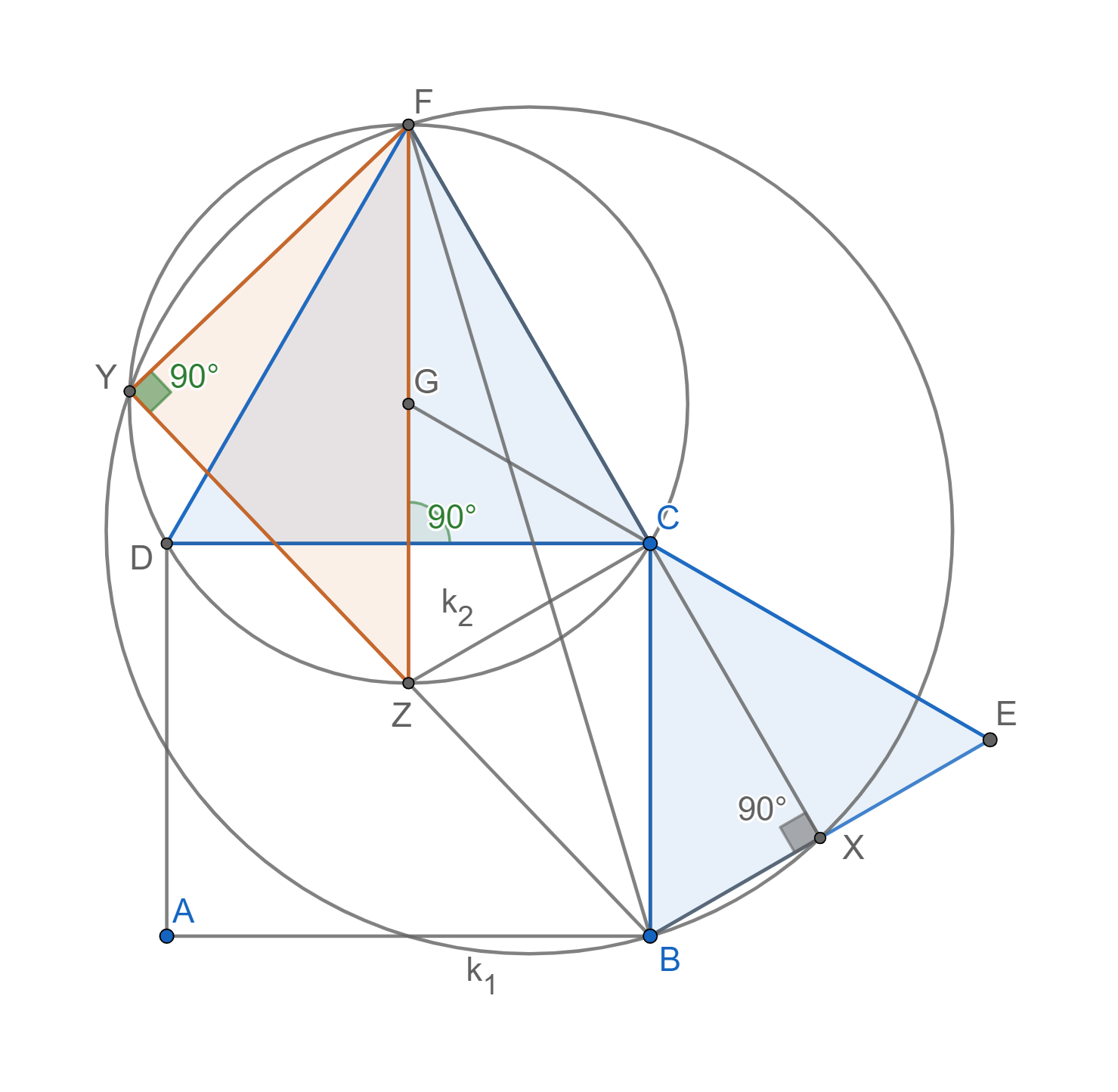
Aktuálne sa vieme zamerať na trojuholník \triangle ZCF. Už vieme, že ZF je prepona. Ide teda podľa Tálesovej vety o trojuholník pravouhlý. Spomeňme si, že \lvert \angle DCF\rvert = 60\degree. Potom ľahko dopočítame, že \lvert\angle ZCD\rvert = 30\degree.

Už sme skoro tam \lvert\angle HCG\rvert= 60/2\degree=30\degreea teraz G je stred kružnice k_2, no úsečka GZ je kolmá na DC a zároveň trojuholníky \triangle HCG a \triangle HCZ sú zhodné podľa vety sus, takže \lvert HG \rvert=\lvert HZ \rvert. G je naozaj obrazom bodu Z pri osovej súmernosti.

Teraz by sme mohli byť šťastní, no ukazuje sa, že v príklade je ešte jeden zakopaný pes. V prípade, že DC\gt\gt BC, poprípade BC\gt\gt DC (postup je úplne rovnaký a nebudeme ho uvádzať) tak trojuholník \triangle DCF vieme preklopiť aj do spodnej roviny tak, aby bod F neležal v obdĺžniku ABCD.

Avšak v tomto prípade tvrdenie zo zadania platiť nemôže, lebo bod Z je v spodnej polrovine od úsečky DC a teda nemôže byť stredom kružnice opísanej FCD. Máte pravdu prísne vzaté to nie je dôkaz :), ale je to jasné.