Riešky tábor - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×8. príklad - Vzorové riešenie
Zadanie
V každom políčku šachovnice 8 \times 8 je napísané celé číslo tak, aby každé číslo bolo aritmetický priemer nejakých dvoch jeho susedných čísel (susedné sú tie, ktorých políčka sa dotýkajú hranou). Koľko najviac rôznych čísel môže byť na šachovnici a ako sa to dá dosiahnuť? Nezabudnite vysvetliť, prečo ich už nemôže byť viac.
Vzorové riešenie
Kľúč k vyriešeniu príkladu bude v zameraní sa na najväčšie a najmenšie číslo. V každom správne vyplnenom štvorci musí existovať nejaké najväčšie číslo a nejaké najmenšie číslo.
Pozrime sa na to bližšie zápisom. Urobme si tvrdenie, že n je najväčšie číslo. Vieme, že ak je nejaké číslo aritmetickým priemerom dvoch čísel, tak jeho vzdialenosť na číselnej osi od oboch týchto čísel je rovnaká.
V správne vyplnenom štvorci ho teda musíme dostať aritmetickým priemerom jeho susedov, teda n = {\frac {(n-x)+(n+x)} {2}}, pričom (n + x) a (n-x) sú niektorí jeho susedia. Ak je však x iné ako 0, tak buď (n -x) alebo (n +x) budú väčšie ako n, čo je spor s tvrdením, že n je najväčšie číslo. Takto sme dokázali, že x = 0. Inými slovami, najväčšie číslo v štvorci (n) môžeme dostať len tak, že urobíme aritmetický priemer jeho dvoch susedov, ktorí sú tiež n.
Všimnime si, že rovnaké tvrdenie sa dá dokázať aj pre najmenšie číslo, a to presne takým istým postupom.
V našom štvorci to znamená, že každé najväčšie číslo n musí susediť s aspoň dvoma číslami n, a rovnako každé najmenšie číslo m musí susediť s aspoň dvoma číslami m.
Takto vieme zistiť, že v každom štvorci budú aspoň tri najväčšie čísla n. Vieme našu podmienku splniť pre všetky tri? Nie, pretože v štvorčekovej sieti platí, že pre ľubovoľné políčko nie sú žiadni jeho susedia navzájom susední. Teda, mohli by sme podmienku splniť pre jedno políčko s n, avšak jeho susedné políčka s n nedokážu byť navzájom susedné.
Čo ak by sme jedno políčko s n pridali? Potom by sme ich už vedeli usporiadať, aby bola splnená podmienka, teda aby každé n susedilo s dvoma inými n, a to takto:
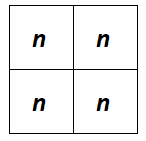
Čo sme si teraz ukázali? Tento náš postup nám dokázal, že pre ľubovoľne správne vyplnený štvorec musí byť počet políčok s najväčším číslom aspoň 4. Rovnaký postup vieme aplikovať pre najmenšie číslo, a teda nám vyjde, že v ľubovoľnom správne vyplnenom štvorci musia byť aspoň 4 políčka s najväčším číslom n a aspoň 4 políčka s najmenším číslom m.
Vieme teda, že aspoň 8 políčok bude zabratých týmito číslami. Keďže sa pýtame na najväčší počet rôznych čísel v štvorci, tak v ak by sa nám zvyšných 56 políčok podarilo vyplniť navzájom rôznymi číslami, určite to bude najlepšie riešenie. Dá sa to?
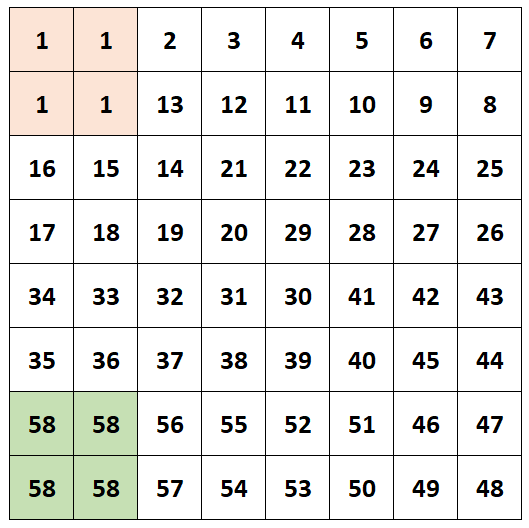
Vyznačené políčka sú políčka s najväčším číslom a políčka s najmenším číslom. Zvyšné políčka sú všetky rôzne, a teda sme našli určite najlepšie riešenie. V tomto riešení máme 58 rôznych čísel.
Nejaká konkrétna konštrukcia sa dala nájsť tak že sme nakreslili ťah, ktorý prechádzal všetkými políčkami okrem minima a maxima tak, že začínal políčkom s najmenším číslom a končil políčkom s najväčším číslom. každé políčko tohto ťahu malo číslo vždy o 1 väčšie ako predošlé políčko. Týmto sme zariadili žepre každé políčko s číslom x platí, že má určite dvoch susedov ktorí majú čísla x-1 a x+1 a ich priemer teda je x