3. príklad - Vzorové riešenie
Zadanie
Máme 8 rovnakých štandardných hracích kociek s číslami 1 až 6 na stenách.
- Dokážeme z nich poskladať kocku 2\times2\times2 tak, aby sa kocky dotýkali stenami s rovnakým číslom?
- Dokážeme to isté ako (a.), aby navyše na povrchu veľkej kocky boli iba 3 rôzne čísla?
Vzorové riešenie
Ako prvé sa pozrime na úlohu a.
Môžme si všimnúť že ak si vezmeme 4 kocky, tak ich vieme usporiadať do štvorca 2 \times 2 takým spôsobom, že navrchu bude mať každá kocka číslo a. Takéto usporiadanie bude vyzerať nasledovne:

Vidíme, že všetky kocky v tomto rozložení sú rovnaké len otočené.
Pri takomto rozložení môžme spraviť z ďaľších štyroch kociek taký istý štvorec a tieto dva štvorce dať stranami s číslami a k sebe a dostaneme kocku, ktorá spĺňa zadanie. To preto, že na prvom "poschodí" vidíme, že sú všetky susediace čísla rovnaké, to znamená že aj na druhom "poschodí" budú susediace čísla rovnaké. Navyše kedže spájame dve štvorice, ktoré majú iba a, tak aj susediace čísla medzi "poschodiami" budú rovnaké.
Pozrime sa teraz na úlohu b.
V tejto úlohe si môžeme všimnúť, že ak dokážeme, že po spojení dvoch kociek nebudeme vedieť dostať na 4 susediacich stranách (2 strany veľkosti 2 \times 1 susediace hranou a 2 strany veľkosti 1 \times 1 oproti sebe) dokopy najviac 3 rôzne čísla, potom nedokážeme vytvoriť kocku tak, aby mala na povrchu iba 3 rôzne čísla. Celá naša kocka sa totiž skladá zo 4 takýchto dvojíc a každá prispieva povrchu práve 4 stenami.
Zoberme dve kocky a priložme ich rovnakým číslom k sebe, nech je toto číslo napríklad 6. Potom na druhej strane každej kocky bude číslo 1. Takže na obvode už mám jedno číslo a strany 2 \times 1 môžu mať dokopy najviac 2 rôzne čísla.
Teraz si môžme všimnúť že ak máme na kocke vľavo čísla na stranách napríklad v poradí 3, 5, 4, 2 tak na kocke vpravo budeme mať čísla v poradí 2, 4, 5, 3. To preto, že ak sú kocky otočené k sebe rovnakým číslom tak jedna je otočená o 180 stupňov (v rovnakom poradí by bola ak by bola zrkadlovo otočená a to by už bola iná kocka), takže aj jej ostatné strany sa otočia. Ak sa teda pozrieme na tie dve strany ktoré susedia spolu tak budú vyzerať nasledovne:
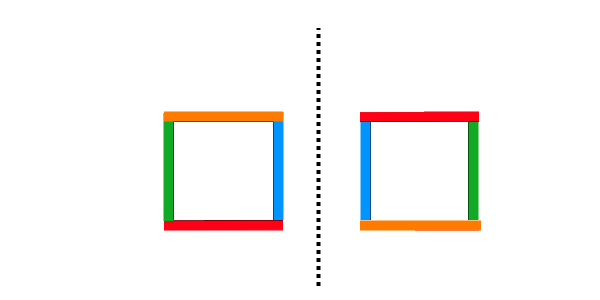
(V obrázku sa pozeráme pri oboch kockách na číslo, ktorým sa dotýkajú takže nám na okrajoch susedia modrá s modrou a zelená so zelenou.)
Z tohto je jasne vidno, že nech jednu z nich otáčame akokoľvek, tak vždy bude platiť že na stranách 2 \times 1 budú buď rôzne čísla, alebo každá druhá strana bude mať rovnaké čísla a každá druhá rôzne. Dokopy sú to vždy aspoň 3 čísla, čo je viac ako môže byť na splnenie zadania.
To znamená že neviem vybrať 2 priľahlé strany tak aby mali na sebe maximálne 2 rôzne čísla. Neviem teda ani vytvoriť kocku 2 \times 2 \times 2 tak, aby spĺňala podmienky úlohy.
Odpoveď:
a) Dokážeme vytvoriť.
b) Nedokážeme vytvoriť.