Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

7. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Na stole je n šálok usporiadaných do kruhu, pod ktorými sú rôzne korenia. Vždy, keď sa Šálka pozerá niekde inde, príde Ján Kuchár a môže mu šálky obrátiť, pootočiť alebo oboje. Obrátenie vyzerá tak, že kruh niekde rozpojí, a zapojí ho na opačnej strane - teda poradie šálok aké bolo predtým v smere hodinových ručičiek bude teraz proti smeru hodinových ručičiek. Príklad obrátenia môžete vidieť aj na obrázku. Okrem toho teda vie celý kruh šálok ľubovoľne otočiť. Nikdy však nezmení, ktoré šálky sú vedľa seba. Šálka našťastie vie, že to Ján Kuchár robí, a keďže si chce zapamätať, kde je ktoré korenie, použil niekoľko rôznych farieb šálok. Aký je najmenší počet rôznych farieb šálok (v závislosti od n), ktoré potrebuje použiť, aby vždy vedel určiť, pod ktorou šálkou je ktoré korenie?

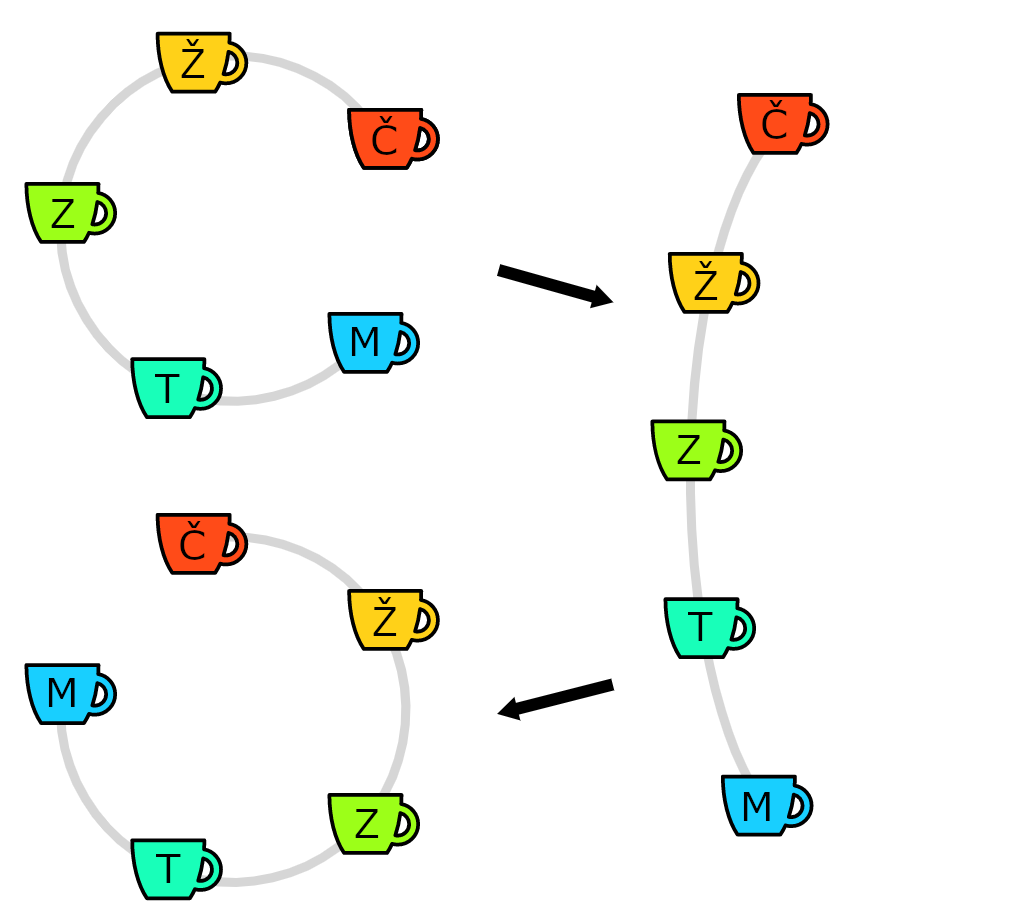
Vzorové riešenie

Opravovali: Susty, duško, erik

Všetky šálky si zafarbíme najskôr rovnakou farbou. Povedzme si, že bude zelená. Ak máme 1 šálku, tak teda budeme potrebovať 1 farbu.

Ak máme 2 a viac šálok tak vieme, že musia byť použité aspoň 2 rôzne farby, lebo ak by mali všetky rovnakú farbu nevedeli by sme ich rozoznať. Povedzme si, že bude modrá. Čiže ak máme 2 šálky potrebujeme 2 farby.

Zafarbili sme si teda jednu šálku na modro. Táto šálka nám hovorí, či boli šálky pootočené. To vieme určiť tak, že sa pozrieme o koľko bola modrá šálka posunutá čiže si vieme povedať, kde bola ktorá šálka.

To by však platilo iba kebyže Kuchár šálky pootáča, on ich však môže aj obrátiť. Na to aby sme vedeli rozoznať, či boli šálky obrátené potrebujeme si nejako označiť smer kruhu. Ako prvé nás napadne zafarbiť suseda modrej šálky na inú farbu, povedzme, že na červenú a dáme ju napravo od modrej. Ak by prišlo k obráteniu šálok, táto červená šálka by susedila s modrou z “opačnej strany” - bola by naľavo od modrej šálky. Čiže pre n≥3 budeme teoreticky potrebovať najviac 3 farby.

Myšlienka s obracaním však ide trochu vylepšiť. Namiesto červenej šálky vieme použiť 2 modré. To by fungovalo tak, že si napravo vedľa modrej necháme zelenú šálku a za ňou budeme mať 2 modré šálky vedľa seba. Tak vieme povedať, či bol zmenený smer, lebo ak by prišlo k obráteniu šálok, tieto dve modré šálky by boli naľavo od tejto jednej modrej šálky. Na to aby sme to vedeli povedať jednoznačne musí byť z druhej strany medzi modrou a 2 modrými šálkami aspoň 2 zelené. Ak by ich bolo 0 tak by sme mali v podstate 3 modré šálky vedľa seba, čiže by sme nevedeli povedať či boli šálky obrátené a kebyže je 1 tak tiež, lebo dvojica modrých šálok je rovnako ďaleko zprava aj zľava čiže tiež nevieme určiť či boli šálky obrátené. Preto toto vylepšenie platí len pre n \geq 6.

Odpoveď: Ak n=1 tak potrebujeme 1 farbu, ak n=2 tak 2, ak n=3;4;5 potrebujeme 3 farby a pre n \geq 6 potrebujeme 2 farby.