Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

4. príklad - Vzorové riešenie

Kategórie:
5
6
7
8

Zadanie

Na strope miestnosti sa nachádza obrovský obrazec skladajúci sa z troch veľkých trojuholníkov, ktoré sú všetky rozdelené na štyri menšie trojuholníčky tak, ako vidíte na obrázku. Do obrazca sa vpisujú do malých trojuholníčkov kladné celé čísla od 1 po 10 vrátane, pričom do každého malého trojuholníčka sa vpíše práve jedno číslo a čísla sa v obrazci nesmú opakovať. Súčty čísel v každom z troch veľkých trojuholníkoch sú rovnaké. Čísla 1, 2, 4 a 10 sú už vpísané do obrazca. Nájdite všetky možnosti ako sa dajú povpisovať zvyšné čísla, aby platili vyššie uvedené podmienky.

Vzorové riešenie

Opravovali: merlin, sarisko

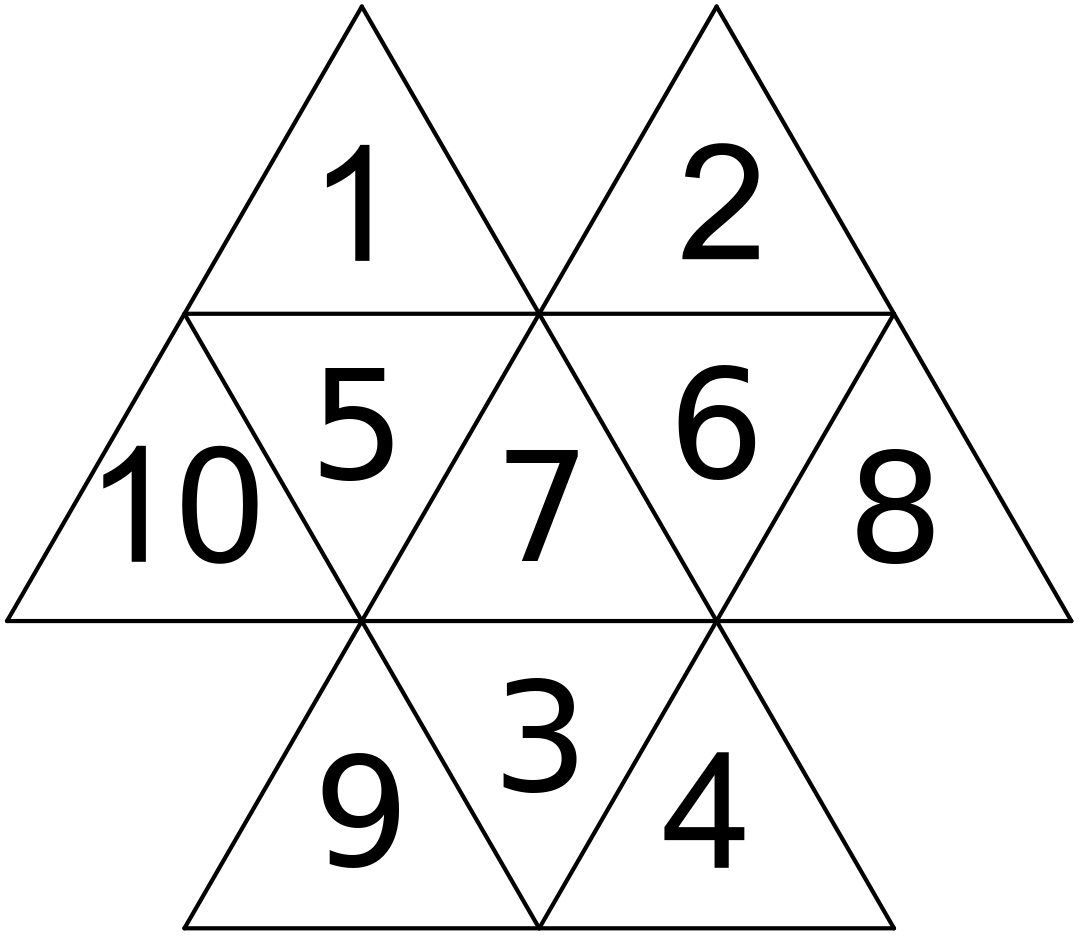
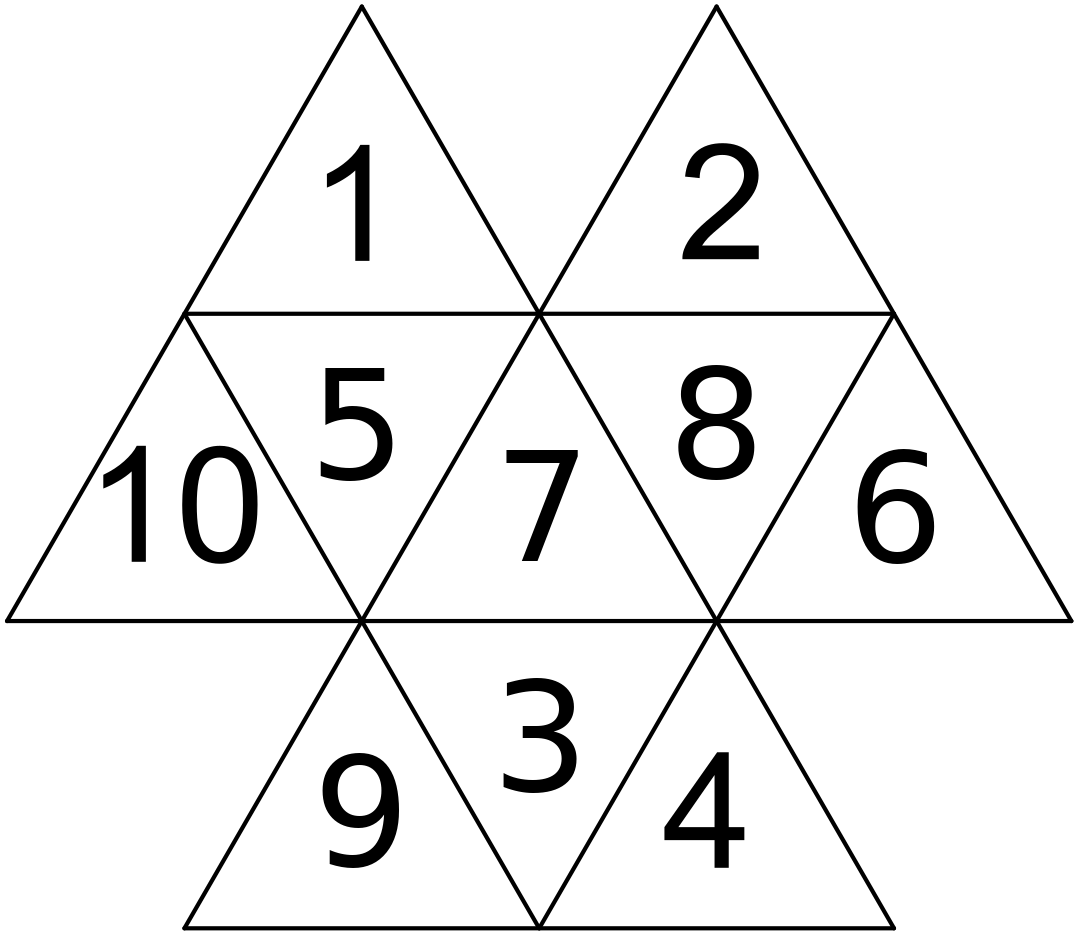
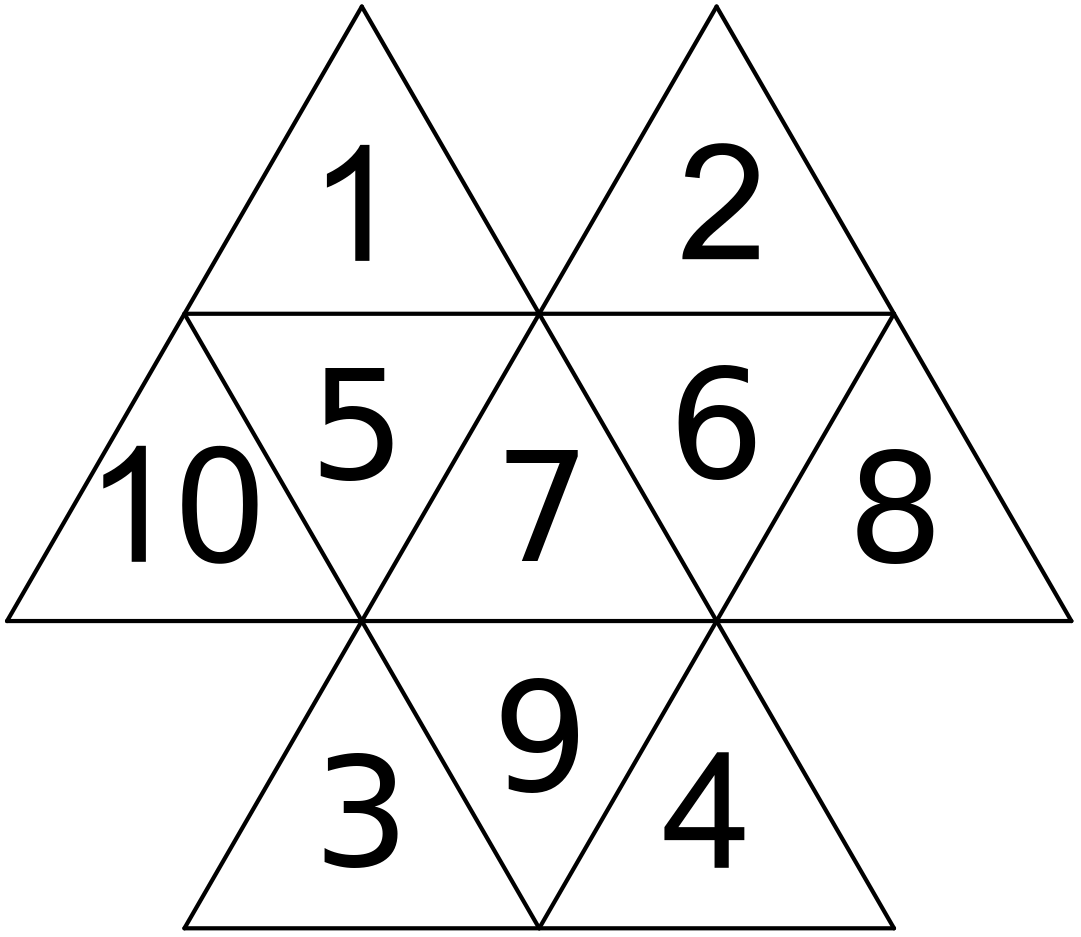
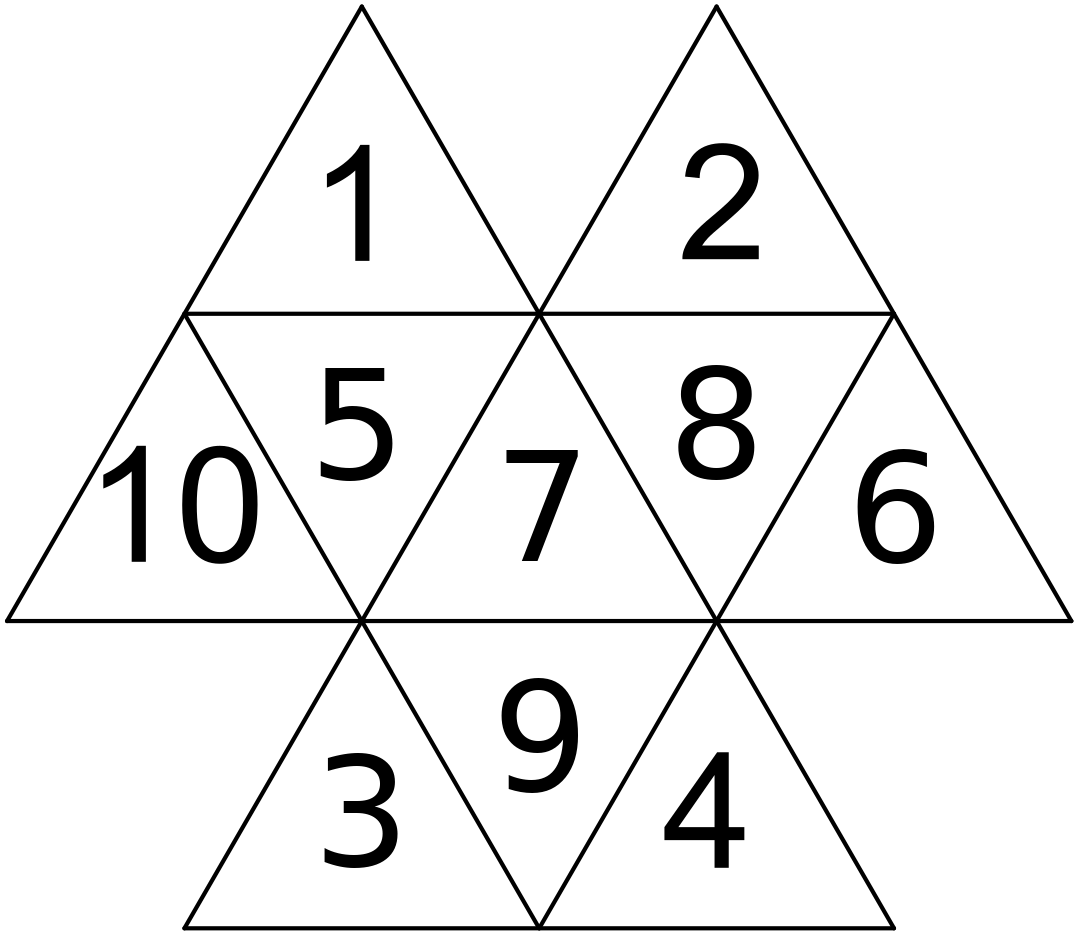
Označme si čísla v jednotlivých trojuholníčkoch ako na obrázku a súčet čísel vo veľkom trojuholníku S. 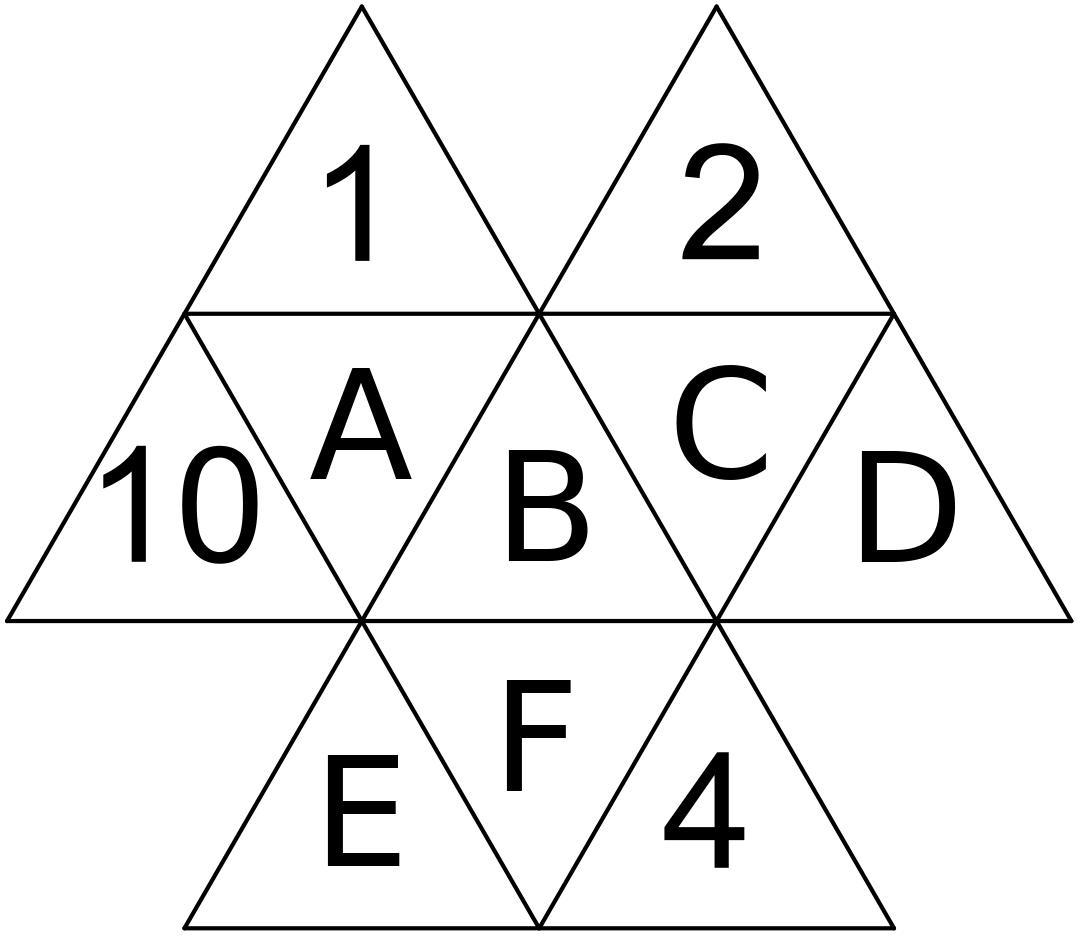Keď sa pozrieme na súčet súčtov čísel v jednotlivých veľkých trojuholníkoch, ktorý je 3S, tak v ňom započítame každé číslo práve raz, okrem čísla B, ktoré započítame 3-krát.
Teda dostávame rovnicu:

3S - 2B = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55,

ktorú upravíme na:

S = \dfrac{55 + 2B}{3}.

Keďže je S celé číslo (čísla v trojuholníčkoch sú len celé čísla, teda aj ich súčet bude celé číslo), tak 55 +2B musí byť deliteľné 3. Keďže zvyšok po delení 3 čísla 55 je 1, tak potom zvyšok čísla 2B po delení 3 musí byť 2. Teda zvyšok B po delení 3 je 1. Podľa zadania tak B môže byť 1, 4, 7 alebo 10. Čísla 1, 4 a 10 už ale máme umiestnené v niektorom z trojuholníčkov, teda B = 7.

Súčet čísel v jednom veľkom trojuholníku je teda S = \frac{55 + 14}{3} = 23. V ľavom hornom veľkom trojuholníku už máme čísla 1, 10 a 7, teda A = 23 - 10 - 1 - 7 = 5.

Z pravého horného veľkého trojuholníka dostávame rovnicu 23 = 2 + 7 + C + D, teda C + D = 14. Keďže nám zostáva umiestniť už len čísla 3, 6, 8 a 9, tak jediná možnosť, ktoré čísla môžu byť C a D je 6 a 8 (je to jedno, v akom poradí).

Zo spodného veľkého trojuholníka dostávame rovnicu 23 = 4 + 7 + E + F, teda E + F = 12. Keďže jediné čísla, čo nám zostali majú súčet 12, tak jediná možnosť, ktoré čísla môžu byť E a F je 3 a 9 (je to jedno, v akom poradí).

Keďže máme 2 dvojice čísel, ktoré sa navzájom môžu vymeniť, tak dostávame 4 možnosti: