Riešky výlet - Ahojte Rieškari, zoberte batohy, úsmevy, dobré nálady, lopty, hry, frisbee, kamarátov… a poďte s nami na výlet! Poprechádzame sa po Malých Karpatoch, kde pre vás máme pripravený skvelý program a … Prejsť na článok
×8. príklad - Vzorové riešenie
Zadanie
- Dokážte, že štvoruholník OPQR je rovnobežníkom.
- Dokážte, že \measuredangle ABC = \measuredangle PQR.
Vzorové riešenie
a)
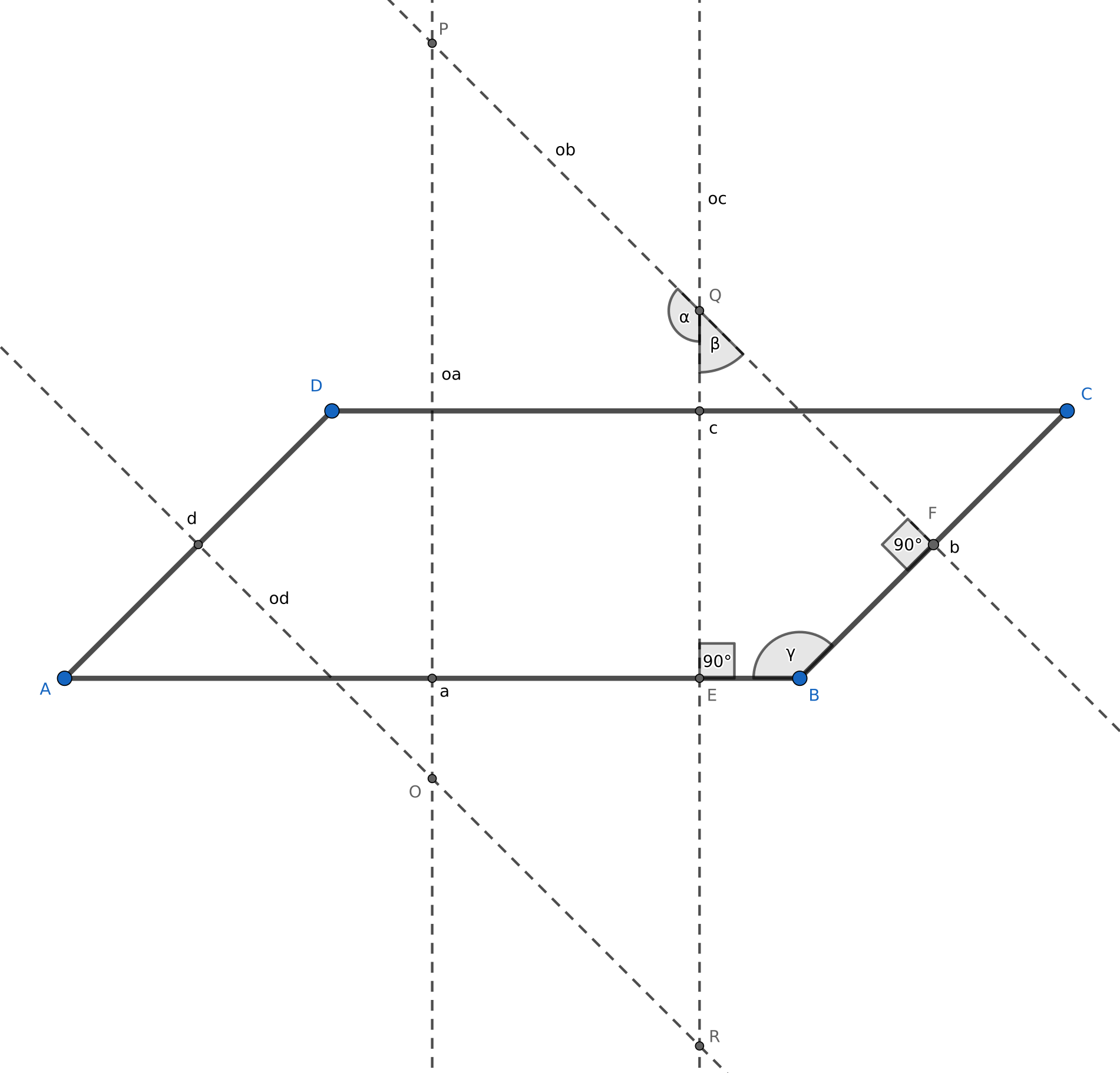
Na obrázku vidíme rovnobežník ABCD. Stred kružnice opísanej trojuholníku je priesečníkom osí strán trojuholníka, avšak stačia nám len dve. V obrázku si označíme osi strán tohto rovnobežníka. Pomocou oa a od zistíme bod O ktorý leží v ich priesečníku, pomocou oa a ob zistíme bod P, ob a oc určuje bod Q a v priesečníku oc a od je bod R. Keďže os strany je kolmica na danú stranu, osi strán budú tiež na seba rovnobežné (kolmice na rovnobežky sú tiež rovnobežné). Tým pádom má vzniknutý útvar OPQR dve a dve protiľahlé strany rovnobežné, čiže to je rovnobežník.
b)
Vo vzniknutom obrázku si vyznačíme bod E, ktorý je priesečníkom oc a úsečky AB, bod F je priesečníkom ob a úsečky BC. Potom si vyznačíme uhly \alpha = \measuredangle PQR, \beta = \measuredangle RQF a ako posledné \gamma = \measuredangle ABC.
Môžme si všimnúť, že \alpha = 180 - \beta, keďže sú to susedné uhly. O uhle \gamma vieme, že je vnútorným uhlom štvoruholníka EBQF. Tiež vieme, že úsečka EQ je kolmá na EB a FQ je kolmá na BF. Keďže vieme, že súčet vnútorných uhlov štvoruholníka je 360\degree, tak odčítame tieto dva pravé uhly a ostane nám, 180 = \beta + \gamma. To vieme upraviť na \gamma = 180 - \beta a keďže \alpha = 180 - \beta vidíme, že \measuredangle OPQ = \measuredangle ABC.
Komentár:
Príklad vás riešilo pomenej, no za to ste ho väčšina veľmi pekne zvládli. Hlavným nedostatkom bývali chyby vo vysvetlení, prípadne niektoré časti neboli vysvetlené vôbec, čo sa odzrkadlilo aj na bodovaní.