Vzorové riešenia 2. kola
1. príklad
Zadanie
Vzorové riešenie
Ako prvé si spočítame počet vypočítaných príkladov za týždeň (za týždeň zakaždým vypočíta rovnaký počet príkladov, je jedno v ktorý deň týždeň začne): 3 + 3 + 3 + 3 + 3 + 5 + 5 = 25
Vieme že vypočítal 111 príkladov (vypočítal od 1. príkladu po 111.) a zistíme koľko príkladov vypočítal za menej ako týždeň:
111 \div 25 = 4, zvyšok 11
Ďalej musíme zistiť ktoré dni majú spolu 11 vypočítaných príkladov:
Keďže 11 nie je deliteľná 3 a ani 5, tak to môže byť iba ich kombinácia (5 + 3 = 8) - ak dáme 5 + 5, tak sa tam nezmestí 3 (5 + 5 + 3 = 13) \Rightarrow musí to byť 5 + 3 + 3 (= 11).
Z tohto vieme, že riešil 4 týždne a 3 dni z toho 2 pracovné a 1 víkendový. \Rightarrow Keďže víkendové dni idú 2 po sebe a my máme len 1, tak buď začíname v nedeľu alebo končíme v sobotu (musíme cez víkend začať alebo skončiť).
Ak si tieto možnosti odskúšame, tak zistíme, že štvrtok + piatok + sobota vychádza (3 + 3 + 5) a aj nedeľa + pondelok + utorok (5 + 3 + 3) \Rightarrow Úloha má dve riešenia.
Odpoveď: Maťko začal vo štvrtok alebo nedeľu.
2. príklad
Zadanie
Vzorové riešenie
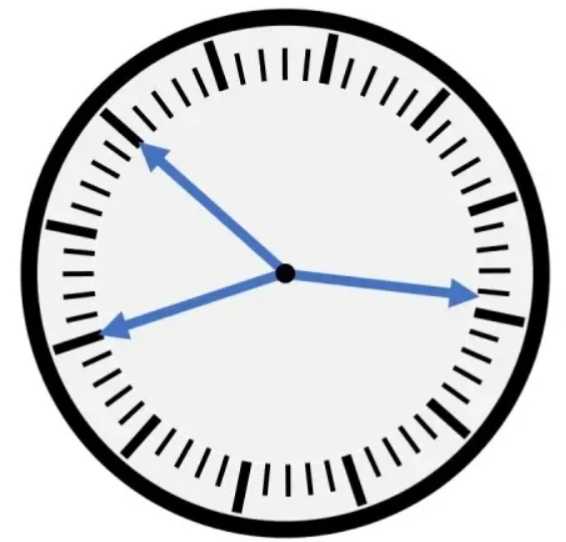
Na začiatok si zistíme, ktorá ručička vlastne plní ktorú funkciu (t.j. ktorá je hodinová, minutová a sekundová).
Je celkom očividné, že ručičky vľavo ukazujú na presný dielik (ten, ku ktorému na hodinových ručičkách pripadajú čísla od 1 do 12). Teda pokiaľ je jedna z týchto ručičiek hodinová, tak druhá z nich musí ukazovať na 12 (lebo je to celá hodina). Ale zároveň je to aj celá minúta, teda posledná ručička, čo nám ostala (tá vpravo), by mala tiež ukazovať na 12, čo sa ale nedeje. Tým sme vylúčili, že by niektorá z ručičiek vľavo bola hodinová a tak sme dospeli k faktu, že práve ručička vpravo bude hodinová.
Teraz si opäť všimneme fakt, že obe zvyšné ručičky, pri ktorých nevieme určiť, či sú sekundové alebo minutové ukazujú na presný dielik. Z toho môžeme usúdiť, že sekundová bude smerovaná na 12, aby sme dostali celú minútu. Teraz sme sa dostali do situácie, kedy je potrebné preskúmať len dve situácie:
1. ručička dole bude sekundová - podľa obrázku si vieme ľahko spočítať, že potom minutová bude ukazovať na číslo 2, čo je zodpovedajúce 10 minútam po celej hodine. Keď sa ale pozrieme na hodinovú ručičku, tak tá ukazuje na menej alebo rovnako ako 12 minút pred celou hodinou, čo znamená, že v tomto prípade nedostaneme správne riešenie
2. ručička hore bude sekundová - podľa obrázku zistíme, že minutová ručička ukazuje na číslo 10, čo je úmerné 50 minútam pred celou hodinou, čo aj pre hodinovú ručičku vyhovuje
Teraz už len spočítame, aký čas bude na hodinovej ručičke a dostaneme riešenie 4 hodiny a 50 minút (pre perfekcionostov je riešenie aj 16 hodín a 50 minút, čo ti však ručičkové hodiny neukážu :) ).
3. príklad
Zadanie
Vzorové riešenie
100=x+y+z
Z toho si vyjadríme z:
z=100 -x -y
Teraz si rovnicou vyjadríme, koľko dukátov Tony minie, keď vieme, že dokopy má minúť 100 dukátov. Rovnica pre dukáty bude potom vyzerať nasledovne:
100= \frac{7}{2}\cdot x + \frac{4}{3}\cdot y +\frac{1}{2}\cdot z
Do tejto rovnice dosadíme za z výraz, ktorý sme si vyjadrili vyššie a rovnicu budeme ďalej upravovať takto:
Keďže Tony kupoval iba celý počet šálok, riep a šošovičiek tak \frac{18}{5}x musí byť celé číslo. To docielime iba tak, že x bude deliteľné piatimi. Potom x môže byť iba 0, 5, 10 alebo 15. X nemôže byť väčšie ako 15, lebo ak by sme si za x dosadili 20 (najmenšie možné ďalšie číslo, ktoré je deliteľné piatimi) tak y=60-\frac{18}{5}\cdot20 \Rightarrow y=60-72= -12 a to je záporné číslo (záporny počet riep si nemôže kúpiť). Čiže ak by bolo x>15, tak by počet riep vyšiel záporný a to sa nemôže stať.
Teraz prejdeme všetkými možnosťami x:
Ak by bolo x=0, tak y = 60-\frac{18}{5}\cdot0 = 60 a z = 100-0-60=40
Ak by bolo x=5, tak y = 60-\frac{18}{5}\cdot5=60-18=42 a z=100-5-42=53
Ak by bolo x=10, tak y = 60-\frac{18}{5}\cdot10=60-36=24 a z=100-10-24=66
Ak by bolo x=15, tak y = 60-\frac{18}{5}\cdot15=60-54=6 a z=100-15-6=92
Možnosti, ako mohol Tony na trhu nakúpiť:
1. 0 šálok, 60 riep a 40 šošovičiek
2. 5 šálok, 42 riep a 53 šošovičiek
3. 10 šálok, 24 riep a 66 šošovičiek
4. 15 šálok, 6 riep a 79 šošovičiek
4. príklad
Zadanie
Zistite obsah Imrovej hlavy (štvoruholníka ABCD).
Vzorové riešenie
Pri rovnoramenných trojuholníkoch platí, že výška na základňu je rovnaká ako jeho ťažnica, čiže pretína základňu na polovicu. To znamená, že keď vytvoríme kolmicu z bodu C na priamku AB, tak tento bod (označme si ho X) bude rovnako vzdialený od A ako od B, lebo je v polovici strany AB. Ako môžeme vidieť, tak strana XB je rovnako dlhá ako CD, čiže strana AB bude dlhá 10\text{cm}\cdot 2 = 20\text{cm}.
O štvoruholníku ABCD vieme povedať, že je pravouhlým lichobežníkom lebo má strany AB a CD rovnobežné a \angle ABC je pravý. No a teraz máme len jednoduchý problém, vyriešiť obsah pravouhlého štvoruholníka. Na to aby sme vedeli obsah potrebujeme vedieť dĺžky oboch základní, čo aj vieme, a dĺžku výšky. Keďže tento lichobežník je pravouhlý pri vrcholoch B a C tak strana BC je rovná jeho výške. Takže si to dosadíme do rovnice na výpočet obsahu lichobežníka a dostaneme:
5. príklad
Zadanie
- ten, ktorý už nemôže spraviť ťah prehrá?
- ten, ktorý už nemôže spraviť ťah vyhrá?
Vzorové riešenie
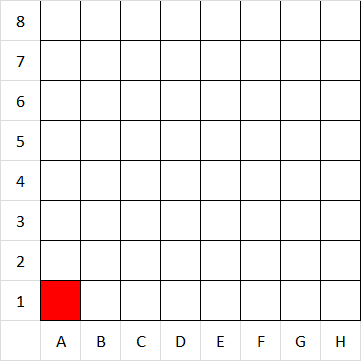
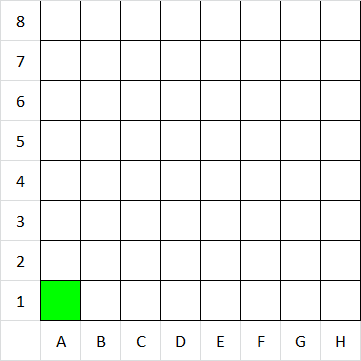
Jediné políčko, z ktorého sa ďalej nevieme pohnúť je políčko A1.
Začneme možnosťou A, v ktorej prehrá hráč, ktorý sa už nedokáže pohnúť. Teda prehrá hráč, ktorý začína svoj ťah na políčku A1. Označme si ho teda červenou (je prehrávajúce).
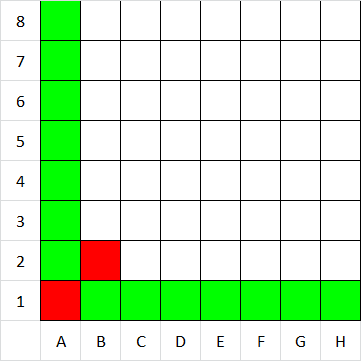
Všetky ostatné políčka v riadku 1 a stĺpci A budú teda víťazné (viem sa z nich pohnúť na prehrávajúce políčko A1). Tieto si označíme zelenou.
Ako si vieme všimnúť vyhrám ak donútim protihráča pohnúť sa na zelené polička. Miesto odkiaľ sa viem dostať len na zelené teda bude prehrávajúce a teda červené.
Ak sa dokážem z políčka dostať na červené potom je políčko zelené.
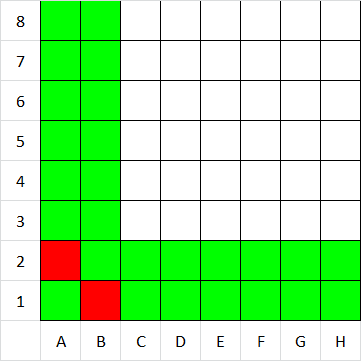
Všimnime si, že takéto políčko z ktorého sa vieme dostať len na zelené je ľavé dolné nevyfarbené a teda B2(bude červené.)
Situácia sa nám teda zopakovala, že si zafarbím na zeleno stĺpec a riadok, z ktorého sa viem na B2 dostať.
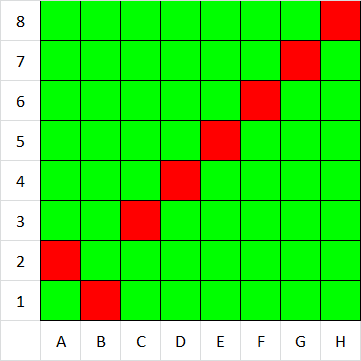
Takýmto spôsobom budem zafarbovať tabuľku.
Vidíme, že červené políčka sú len na uhlopriečke. Takže vyhrám ak sa presuniem na uhlopriečku. Keďže Adam začína na uhlopriečke a nemôže sa hýbať šikmo nemôže sa presunúť na uhlopriečku. Šošo sa na uhlopriečku dostane tak, že ak Adam pôjde o n poličok tak Šošo pôjde o n políčok do druhého smeru (ľavo/ dole).
Teda Šošo má víťaznú stratégiu.
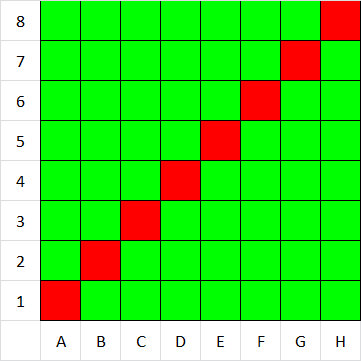
Postupné ofarbovanie šachovnice (Možnosť A)
Ak sa hráč nevie už pohnúť, tak vyhral. Teda políčko A1 je vyhrávajúce (zafarbíme ho na zeleno).
Teraz existujú 2 políčka, z ktorých sa dokážem pohnúť len na políčko A1, a to B1 a A2. Tie sú teda prehrávajúce a zafarbíme ich na červeno.
Teraz si môžem všetky políčka v riadkoch 1 a 2 a v stĺpcoch A a B (okrem políčok B1 a A2) zafarbiť na zeleno, lebo sa z nich dokážem posunúť na červené políčko.
Tabuľku ďalej budeme ofarbovať pomocou rovnakých pravidiel, ako v možnosti A.
Ako si môžme všimnúť, Adam sa na začiatku môže pohnúť len na zelené políčka, teda Šošo má znova výhernú stratégiu (bude sa stále posúvať na prehrávajúce políčka).
Postupné ofarbovanie šachovnice (Možnosť B)
6. príklad
Zadanie

Vzorové riešenie

Obr. 1: Označenie strán a výšky

Obr. 2: Výšky v trojuhlníkoch
8 = \dfrac{a \cdot v_2}{2}
? = \dfrac{a \cdot v_1}{2}
Súčet ich obsahov teda bude:
8 + ? = \dfrac{a \cdot v_2}{2} + \dfrac{a \cdot v_1}{2} = \dfrac{a \cdot v_1 + a \cdot v_2}{2} = \dfrac{a \cdot \left(v_1 + v_2 \right)}{2}
Vráťme sa späť k druhému obrázku. Vidíme, že výšky v_1, v_2 sú kolmé na protiľahlé strany rovnobežníka. Taktiež vidíme, že sa stretajú v jednom bode. Ich spojením teda dostaneme výšku na stranu a v našom rovnobežníku - v. My teda vieme, že obsah našich dvoch trojuholníkov je 8 + ? = \dfrac{a \cdot \left(v_1 + v_2 \right)}{2} = \dfrac{a \cdot v}{2}, čo je polovica obsahu nášho rovnobežníka.
Aký má teda obsah celý náš rovnobežník? Keď sme práve zistili polovicu obsahu, vieme povedať, že celý obsah bude 2 \cdot \left(8 + ?\right). Keďže je však v zadaní rozdelený na štyri trojuholníky, vieme ten istý obsah vyjadriť aj ako súčet obsahov týchto menších trojuholníkov: 5 + 8 + 6 + ?. Obe hodnoty sú obsahom rovnobežníka, takže sa musia rovnať.
7. príklad
Zadanie
Vzorové riešenie
Označme si najprv cenu dospeláckeho lístka a a cenu detského lístka ako c. Potom ak p, q budú prvočísla a x, y budú kladné celé čísla, tak potom zadanie nám poskytuje nasledovné dve rovnice:
Práve tieto p^x, q^y, to je definícia toho, čo je kladná mocnina prvočísla. To, že je kladná a nie nulová, vyplýva z toho, že p^0 = 1 a v tom prípade by musel stáť aspoň jeden typ lístka menej ako 1, čo je v rozpore so zadaním.
Ak dve čísla v súčine sú mocnina prvočísla, tak aj samotné čísla musia byť mocninami toho istého prvočísla. To vyplýva z vlastností prvočísel a prvočíselných rozkladov. Zároveň vieme, že opať ani jedna táto mocnina nesmie byť nultá, lebo by sme mali vstupenku s cenou 1. Preto, ak k,m sú kladné celé čísla, vieme zapísať a = q^k, b = q^m.
Dosadením tohto poznatku do rovnice so súčtom máme:
Teraz môžeme celú rovnicu vydeliť q^m, získame q^{k-m} + 1 = q^{x-m}. Zároveň si môžeme byť istí, že x-m \geq 1, inak by bola druhá vstupenka zápornej (alebo nulovej) ceny, čo nemôže. V tom prípade q^{x-m} je kladná mocnina prvočísla q.
Ak teraz by bolo číslo q nepárne, tak jeho nezáporná mocnina q^{k-m} by bola nepárna a rovnako tak aj jeho kladná mocnina q^{x-m}. Lenže potom by sme mali rovnicu nepárne + 1 = nepárne, čo nemôže nastať.
Preto je q párne číslo. Vzhľadom na to, že q je zároveň prvočíslo, nutne platí, že q = 2. V tom prípade máme na pravej strane rovnice párne číslo a na ľavej strane máme 2^{m-k}+1. Na to, aby tento súčet bolo párne číslo, musí byť 2^{m-k} nepárne. Jediná nepárna mocnina dvojky je 1 a to sa stane práve vtedy, ak m = k.
Jediná vhodná možnosť je teda taká, že cena detskej a dospeláckej vstupenky je rovnaká a navyše sú to kladné mocniny dvojky.
* Poznámka: to, že je to bez ujmy na všeobecnosti, vieme z toho, že tá rovnica je symetrická v tých dvoch premenných. Ak by bola nerovnosť medzi nimi naopak, nič v postupe by to nezmenilo, iba značenie.
8. príklad
Zadanie
- si vopred vyberie jednu z možných ciest a tej sa bude držať,
- na každej križovatke, kde má voľbu dvoch možností, si vyberie jednu s rovnakou pravdepodobnosťou ako druhú?

Vzorové riešenie
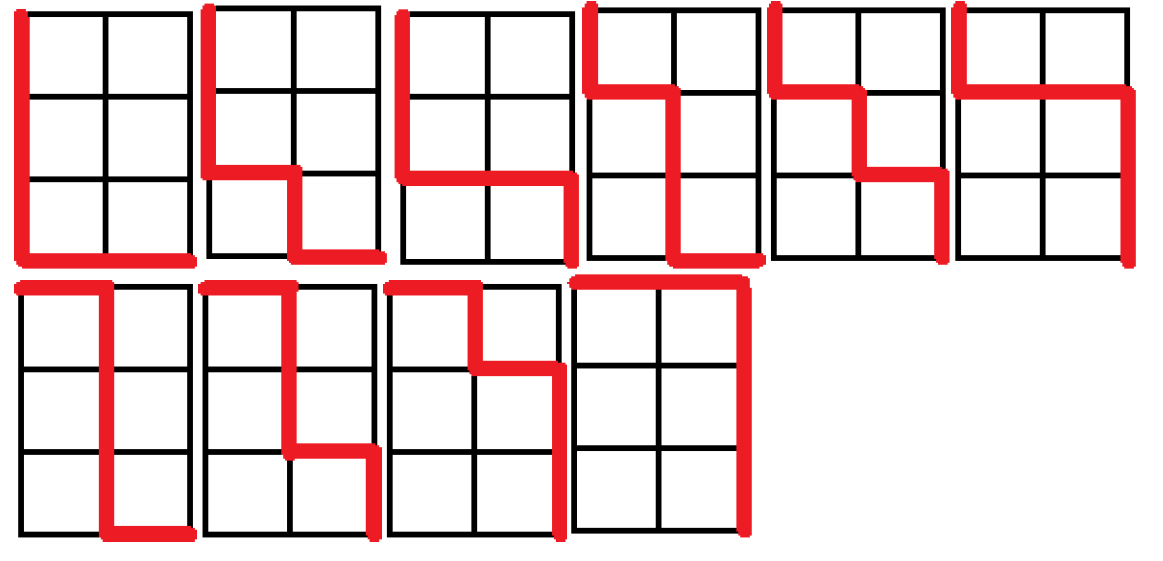
P=\frac{6}{10}=60\%.
Časť A sme zvládli, vrhnime sa preto do časti B. Ako je napísané v zadaní, budeme to riešiť tak, že v každom bode, z ktorého vedú dve cesty, rozdelíme pravdepodobnosť kam Miško pôjde. Najlepšie je to vidieť, ak si to budeme zakraslovať priamo do obrázku:
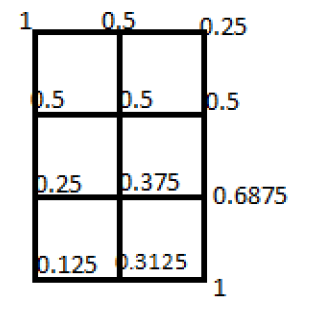
Komentár:
Je dôležité si uvedomiť, že pravdepodobnosti v časti A a B nie sú rovnaké. Rovnako je ale dôležité si aj uvedomiť, prečo nie sú rovnaké. Tieto úvahy nechávame na čitateľa, ale prezradíme, že jedným zo spôsobov, ako si uvedomiť prepojenie výsledkov časti A a B vedie cez Pascalov trojuholník.
9. príklad
Zadanie
Vzorové riešenie
 Najskôr si označíme body tak ako na obrázku. To znamená, že A bude vrchol pri pravom uhle, |AB| bude 40\text{mm} a C je zvyšný vrchol. Potom dotyky kružnice vpísanej so stranami trojuholníka BC, CA, AB označíme postupne D,E,F tak ako na obrázku. Stred vpísanej kružnice označíme S.
Najskôr si označíme body tak ako na obrázku. To znamená, že A bude vrchol pri pravom uhle, |AB| bude 40\text{mm} a C je zvyšný vrchol. Potom dotyky kružnice vpísanej so stranami trojuholníka BC, CA, AB označíme postupne D,E,F tak ako na obrázku. Stred vpísanej kružnice označíme S.
Vieme ukázať, že trojuholníky BSF, BSD sú zhodné podľa SSU, lebo majú rovnakú dĺžku SF, SD (polomer kružnice), pravý uhol pri F, resp. D a oba zdieľajú úsečku BS. Pravý uhol prišiel z toho, že spojnica stredu a bodu dotyku je kolmá na dotyčnicu. Analogicky však aj dvojice CSD, CSE a ASE, ASF sú navzájom zhodné.
Obsah trojuholníka vieme vyrátať dvomi spôsobmi:
- Ako polovica súčinu odvesien, teda \frac{|AB||AC|}{2}
- Ako súčet obsahov trojuholníkov ACS, BCS, ABS, čo je rovné r \cdot \frac{|AB|+|BC|+|CA|}{2}, kde r je polomer vpísanej kružnice, teda 15\text{mm}. Bližšie si to vieme priblížiť tak, že napríklad obsah trojuholníka ABS je \frac{|AB|\cdot v_S}{2}, kde v_S je dĺžka výšky z bodu S, teda |BF|.
Polomer kružnice vpísanej je 15\text{mm}, teda |AF| = |AE| = 15\text{mm}. Potom však |BD| = |BF| = 25\text{mm}, lebo |AF|+|BF| = 40\text{mm}. Jediné úsečky, ktorých nepoznáme dĺžku teda sú CE, CD. Vieme, že zo zhodnosti trojuholníkov CSE, CSD sú rovnako dlhé, teda označme túto dĺžku x. Porovnáme dva spôsoby výpočtu obsahu:
Prémia 1
Zadanie
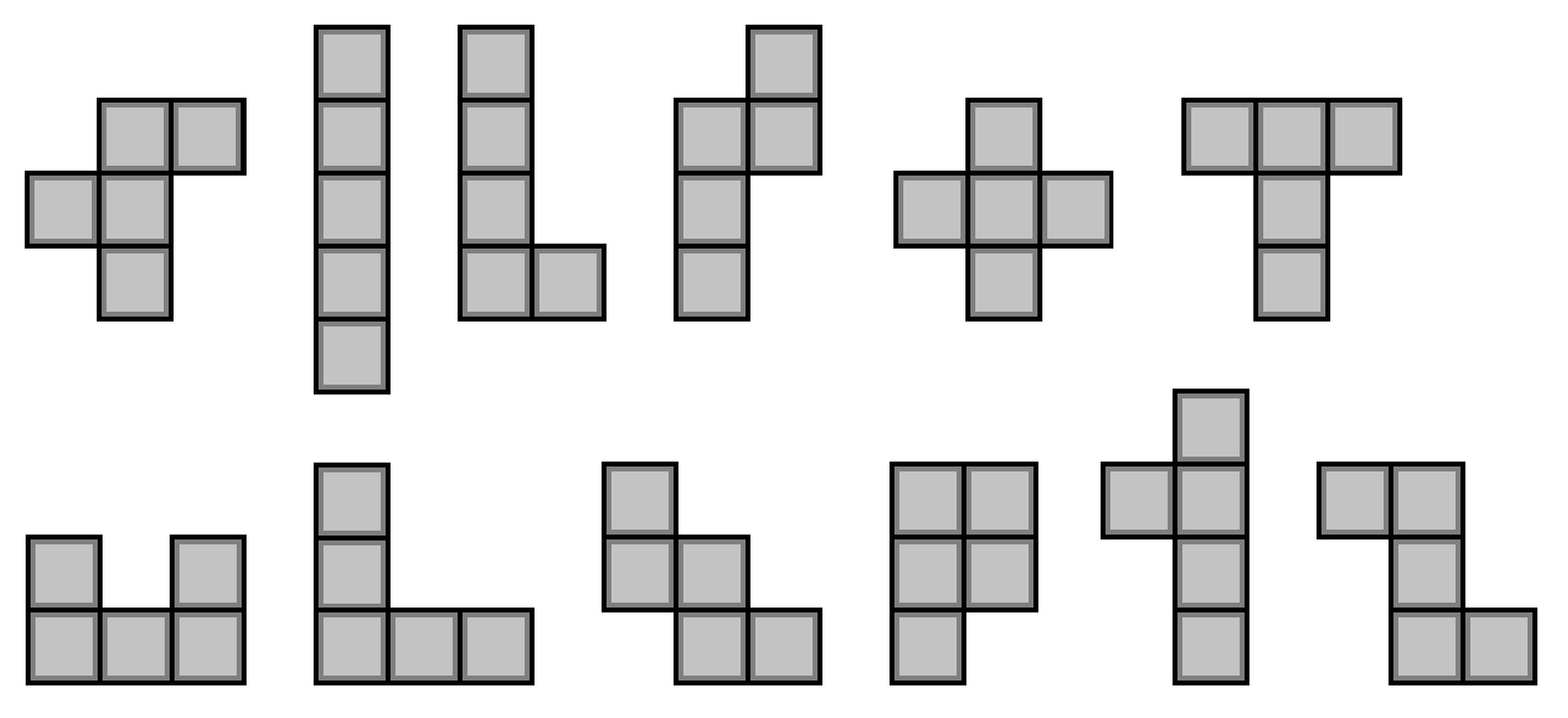
Vzorové riešenie
Najviac sa dalo ohraničiť 128 políčok. Dalo sa to napríklad takto:
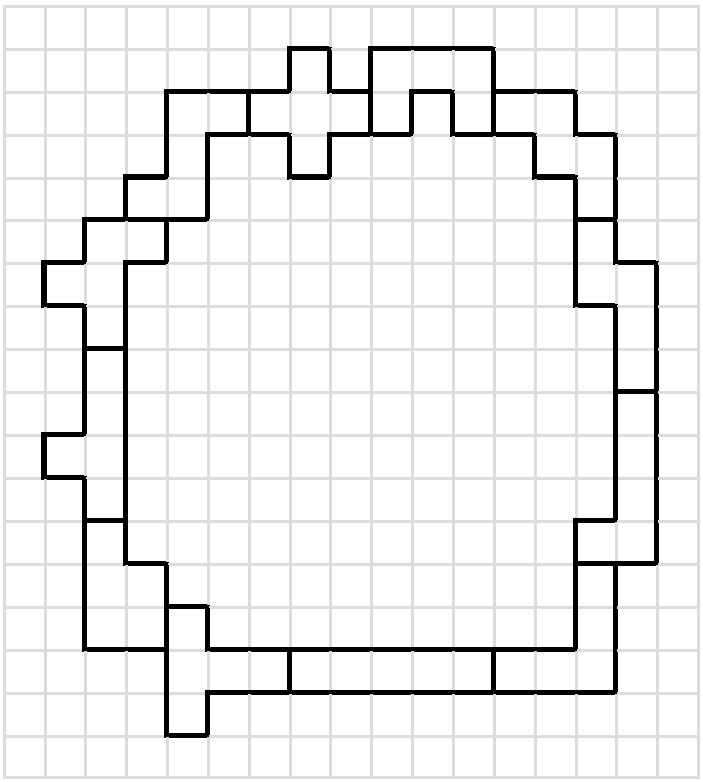 Úlohu sme bodovali podľa toho, koľko políčok ste ohraničili:
Úlohu sme bodovali podľa toho, koľko políčok ste ohraničili:128 - 7 bodov
nad 124 - 6 bodov
nad 114 - 5 bodov
nad 100 - 4 body
nad 95 - 3 body
nad 75 - 2 body
menej - 1 bod