Odporúčaný článok
Presun Riešky výletu - Ahojte, milí riešitelia! Veríme, že rovnako ako my s tešíte na výlet, ktorý mal byť už túto nedeľu. Bohužiaľ z dôvodu predpokladaného nepriaznivého počasia sme sa rozhodli výlet o týždeň … Prejsť na článok
×8. príklad - Vzorové riešenie
Kategórie:
5
6
7
8
9
Zadanie
Ela s Miškom sa pohádali, a teraz sa nechcú vidieť. Miško sa ale chce dostať za Maťkom, aby sa z toho vyrátal. Problém však je, že cestou môže stretnúť Elu. Chce ísť čo najrýchlejšie preto chodí iba dole a doprava. Aká je šanca, že ju stretne, ak
- si vopred vyberie jednu z možných ciest a tej sa bude držať,
- na každej križovatke, kde má voľbu dvoch možností, si vyberie jednu s rovnakou pravdepodobnosťou ako druhú?
Vzorové riešenie
Opravovali: duško, ľubo, šálka
Začnime časťou A. Vieme, že pravdepodobnosť dostaneme ako počet vyhovujúcich udalostí predelený celkovým počtom udalostí. V našom prípade pre pravdepodobnosť, že Miško stretne Elu, budeme mať pomer ciest, na ktorých Elu stretne k celkovému počtu ciest. Vykreslením všetkých ciest dostaneme nasledovné:
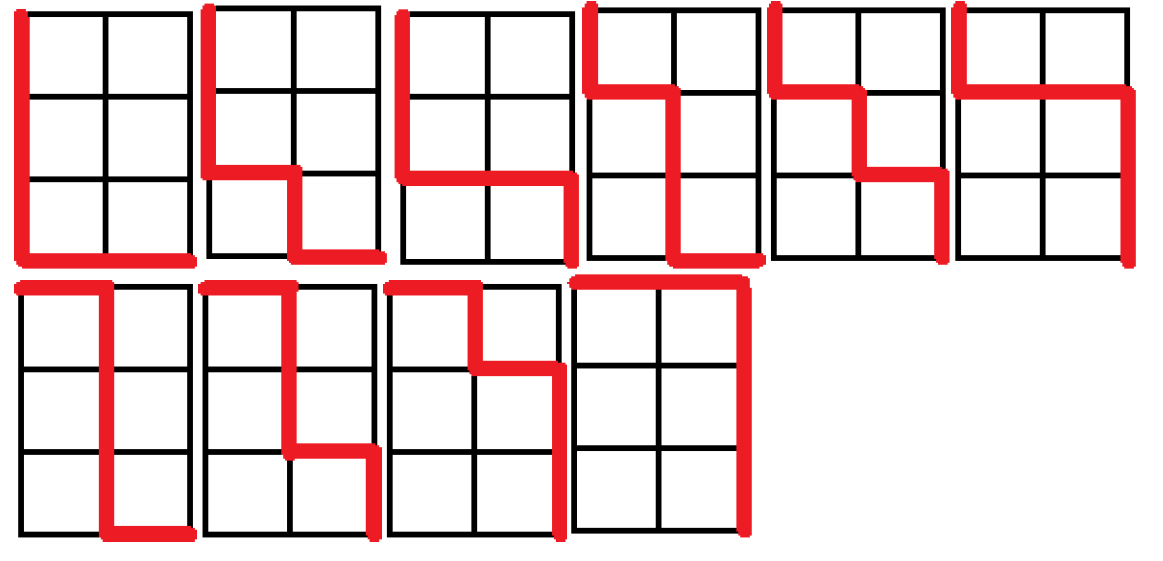Vidíme, že celkový počet ciest, po ktorých Miško môže ísť je 10 z čoho 6 prechádza cez Elu. Pravdepodobnosť toho, že stretne Elu je preto:
P=\frac{6}{10}=60\%.
Časť A sme zvládli, vrhnime sa preto do časti B. Ako je napísané v zadaní, budeme to riešiť tak, že v každom bode, z ktorého vedú dve cesty, rozdelíme pravdepodobnosť kam Miško pôjde. Najlepšie je to vidieť, ak si to budeme zakraslovať priamo do obrázku:
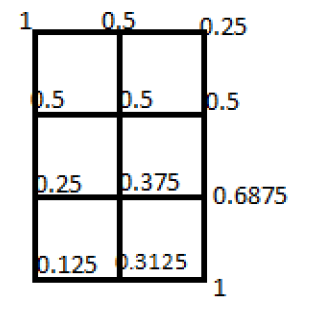Na obrázku je vidieť, že pre cesty sme vždy rozdelili pravdepodobnosť bodu, z ktorého vychádzajú na polovicu. Pre body zase naopak platí, že pravdepodobnosť Miškovho výskytu je súčet pravdepodobností na cestách, ktoré do bodu smerujú. Takýmto spôsobom ľahko vidíme, že pri Ele je pravdepodobnosť Miškovho výskytu 37,5%, čo sme mali za úlohu zistíť.
Komentár:
Je dôležité si uvedomiť, že pravdepodobnosti v časti A a B nie sú rovnaké. Rovnako je ale dôležité si aj uvedomiť, prečo nie sú rovnaké. Tieto úvahy nechávame na čitateľa, ale prezradíme, že jedným zo spôsobov, ako si uvedomiť prepojenie výsledkov časti A a B vedie cez Pascalov trojuholník.
P=\frac{6}{10}=60\%.
Časť A sme zvládli, vrhnime sa preto do časti B. Ako je napísané v zadaní, budeme to riešiť tak, že v každom bode, z ktorého vedú dve cesty, rozdelíme pravdepodobnosť kam Miško pôjde. Najlepšie je to vidieť, ak si to budeme zakraslovať priamo do obrázku:
Komentár:
Je dôležité si uvedomiť, že pravdepodobnosti v časti A a B nie sú rovnaké. Rovnako je ale dôležité si aj uvedomiť, prečo nie sú rovnaké. Tieto úvahy nechávame na čitateľa, ale prezradíme, že jedným zo spôsobov, ako si uvedomiť prepojenie výsledkov časti A a B vedie cez Pascalov trojuholník.