Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

7. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Úloha, ktorú dal Miške výťah, bola veľmi jednoduchá. Do kruhových políčok na obrázku (obr. 2) mala Miška doplniť čísla 1, 2, ..., 9. Každé z nich sa mohlo použiť práve raz. Aby to ale nebolo také ľahké, šesť súčtov troch, respektíve štyroch čísel v políčkach na každej čiare museli byť zhodné. Miška mala povedať aké môžu byť čísla vo vrchnom krúžku. Dokážete to aj vy? Nájdite všetky čísla, ktoré môžu byť vo vrchnom krúžku a nezabudnite pre každé nájsť aspoň jeden prípad, kedy aj naozaj bude vo vrchnom krúžku.

Obr. 2: Políčka

Vzorové riešenie

Opravovali: Paľo

Nazvime si dve čiary spájajúce po štyri krúžky riadky a štyri čiary spájajúce po tri krúžky stĺpce. Taktiež si uvedomme, že súčet čísel 1 až 9 je rovný 45, označme si neznámy súčet na každej čiare ako S a ešte nech cifra na vrchu je x.

Všimnime si, že dva riadky spolu s krúžkom navrchu používajú každý krúžok práve raz. Teda neznámy súčet S vieme zistiť ako S = \frac{45-x}{2}.

Ďalej sa zamerajme na stĺpce. Všetky zasahujú do vrchného políčka, takže ak ho na chvíľu odignorujeme, súčty v stĺpcoch zostanú stále rovnaké. Presnejšie, vzniknú nám štyri dvojice, ktoré musia mať rovnaký súčet. Ak k tomuto rovnakému súčtu teraz pripočítame x, získame opäť súčet na všetkých čiarach. Rovnicou povedané S = \frac{45-x}{4}+x.

Máme teda dve rovnice, ktorých ľavé strany sú náš neznámy spoločný súčet S. To znamená, že aj pravé strany sa musia rovnať, teda S = \frac{45-x}{2} = \frac{45-x}{4}+x.

Všimnime si, že toto je jednoduchá rovnica s jednou neznámou, a tou je neznáma cifra na vrchu pyramídy. Upravujme teda. Začnime vynásobením číslom 4, získame 90-2x = 45-x+4x. Neznámu x osamostatníme na jednej strane 45 = 5x, z čoho je zjavne vidieť, že x = 9.

Ešte sa musíme presvedčiť, že sa to s deviatkou navrchu dá. Zatiaľ sme totiž iba ukázali, že pre žiadne iné číslo sa to nedá. S vedomosťou, že súčet na každej čiare je 18 (čo zistíme napríklad pomocou S = \frac{45-9}{2} = 18) a trochu hrania sa môžeme nájsť napríklad takéto vyplnenie:

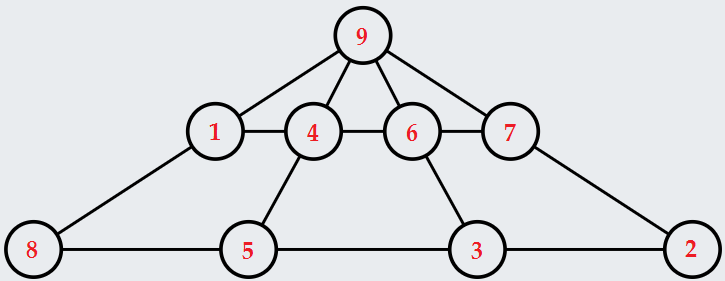
Obr. 1: Príklad vyplnenia všetkých krúžkov

Jediné číslo, ktoré môže byť vo vrchnom políčku je 9.