6. príklad - Vzorové riešenie

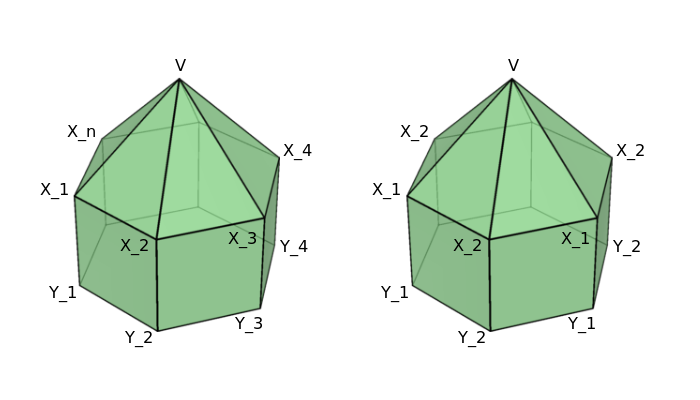
V prvom rade si označíme niektoré veci. Počet vrcholov (= počet strán) podstavy ihlanu budeme značiť n. Hodnotu v hornom vrchole ihlanu označíme v. Hodnoty vrcholov v podstave ihlanu nazveme postupne x_1, x_2, \dots, x_n. Na záver vrcholy v dolnej podstave hranola označíme y_1, y_2, \dots, y_n. (viď ľavý obrázok)

Teraz sa pozrime na ľubovoľné dve susedné steny ihlanu. Majú spoločný jeden horný vrchol s hodnotou v a jeden dolný vrchol s hodnotou x_{i}. Keďže majú ale steny rovnaký súčet musia mať aj zostávajúce nespoločné vrcholy rovnakú hodnotu. (Napr. ak x_{i} = x_2, tak to znamená, že x_1 je to isté ako x_3). Z toho vyplýva, že hodnoty vo vrcholoch podstavy ihlanu sa na preskačku striedajú. Inými slovami, x_1 = x_3 = x_5 = \dots a x_2 = x_4 = x_6 = \dots. Dokonca si môžeme všimnúť, že ak n (počet vrcholov podstavy ihlanu) je nepárny, tak predchádzajúce odvodenie hovorí, že musia byť všetky hodnoty vo vrcholoch podstavy rovnaké, teda x_1 = x_2 = x_3 = \dots.

Podobnú úvahu môžeme urobiť aj pre bočné steny hranola. Každá bočná stena hranola obsahuje 4 vrcholy - dva z hornej podstavy a dva z dolnej. Navyše, tie dva z hornej majú v nejakom poradí hodnoty x_1, x_2 a teda majú súčet x_1+x_2. Pozrime sa teraz na dve susedné bočné steny. Majú spoločný jeden vrchol v dolnej podstave y_i. Zároveň každá má dva vrcholy v hornej podstave, ktoré v súčte dávajú x_1+x_2. A obe steny majú rovnaký súčet. To ale znamená, že ich nespoločné vrcholy v dolnej podstave musia mať rovnakú hodnotu. Aj v dolnej podstave to teda bude vyzerať na preskačku: y_1 = y_3 = y_5 = \dots a y_2 = y_4 = y_6 = \dots. A v prípade, že je n nepárne, sú všetky hodnoty v dolnej podstave rovnaké.

Čo sa to deje ak n je nepárne? Dostávame v celom obrázku najviac 3 rôzne hodnoty v (úplne navrchu), x_1 (v podstave ihlanu) a y_1 (v dolnej podstave hranola). Lenže podľa zadania tam majú byť aspoň 4 hodnoty: 7, 8, 9, 216. n nepárne teda nevychádza a ďalej teda predpokladáme, že n je párne.

Situáciu máme znázornenú na pravom obrázku. Ostalo nám 5 rôznych nezámych v, x_1, x_2, y_1, y_2. Máme im priradiť 5 hodnôt 7, 8, 9, 216, H. Aby sme zistili, čo priradiť čomu, poďme vyjadriť súčty na jednotlivých stenách útvaru:

• trojuholníková stena na ihlane má vždy súčet v+x_1+x_2,
• štvorcová bočná stena hranola má vždy súčet x_1+x_2+y_1+y_2,
• spodná stena podstavy hranola má súčet (y_1+y_2) \cdot\dfrac{n}{2}.

Všetky tieto výrazy majú podľa zadania rovnakú hodnotu.

Z rovnosti prvých dvoch výrazov vyplýva v = y_1+y_2. Z tohto vzťahu vidíme, že jedno z čísel v, y_1, y_2 je H, lebo medzi číslami zo zadania nie sú tri také, že jedno je súčet zvyšných dvoch. Potom ale čísla x_1, x_2 sú obe niektoré zo štyroch zadaných čísel.

Pozrime sa na rovnosť druhého a tretieho výrazu. Dostávame x_1+x_2+y_1+y_2 = (y_1+y_2) \cdot\dfrac{n}{2} a upravíme do tvaru x_1+x_2 = (y_1+y_2)(\dfrac{n}{2}-1). Keďže počet vrcholov podstavy n je aspoň 4, pravá strana rovnice je aspoň (y_1+y_2). Takže aj ľavá strana rovnice musí byť, inými slovami x_1+x_2 \geq y_1+y_2.

Ďalej si všimneme, že x_1 alebo x_2 je 216. Ak by to tak nebolo, tak x_1+x_2 by bolo najviac 8+9 = 17. Avšak y_1, y_2 alebo v = y_1+y_2 by muselo byť 216 a teda by platilo y_1+y_2 \geq 216. Tým by ale bola porušená nerovnosť odvodená v predošlom odseku. Keďže x_1, x_2 sú z pohľadu riešenia zameniteľné, môžeme si povedať, že x_1 = 216.

Ostáva doriešiť 3 možnosti pre x_2:

• x_2 = 7: Vidíme, že v \geq y_1, y_2. Tu preto vznikajú dve možnosti y_1 = 8, y_2 = 9, v = H a y_1 = 8, y_2 = H, v = 9. V prvej vychádza v = y_1+y_2 = 17. Avšak vieme, že (y_1+y_2)\cdot\dfrac{n}{2} = (x_1+x_2+y_1+y_2), teda (ak vyjadríme n) máme n = \dfrac{2(x_1+x_2+y_1+y_2)}{y_1+y_2}. Dosadíme: n = \dfrac{2\cdot(7+216+8+9)}{8+9}, čo ale nie je celé číslo. V druhej možnosti H = 9-8 = 1. Potom použijeme rovnaký vzťah pre výpočet n a dostaneme n = \dfrac{2\cdot(7+216+8+1)}{8+1}, čo ale opäť nie je celé číslo. Takže v tejto vetve nemáme žiadne riešenia.
• x_2 = 8: Opäť využijeme v \geq y_1, y_2 a tak stačí preveriť y_1 = 7, y_2 = 9, v = H a y_1 = 7, y_2 = H, v = 9. V oboch prípadoch odvodíme hodnotu H a použijeme vzorec pre n. Prvá možnosť dáva riešenie n = 30. Skutočne n = 30, x_1 = 216, x_2 = 8, y_1 = 7, y_2 = 9, v = 16 je riešenie. Druhá možnosť (podobne ako v predošlom bode) nevýjde.
• x_2 = 9: Opäť preveríme y_1 = 7, y_2 = 8, v = H a y_1 = 7, y_2 = H, v = 8. Znova vykonáme ten istý postup. Prvá možnosť vedie k riešeniu n = 32. Skutočne n = 32, x_1 = 216, x_2 = 9, y_1 = 7, y_2 = 8, v = 15 je riešenie. Druhá možnosť nevýjde.

Riešením sú teda 30 a 32.