Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

6. príklad

Koniec: 06. apríl 2020 22:00
Do konca: kolo skončilo
Kategórie:
5
6
7
8
9
“Je tu zaznamenané, že nás na túto planétu niekto pritiahol nejakým magnetickým paprskom. Sú tu aj približné súradnice” “Mali by ste sa tam čo najskôr pozrieť” povedal ihneď Jerguš “Ja tu zostanem a pokúsim sa zistiť, kto by nám niečo takéto mohol spraviť. Časť stroskotancov sa teda začala pripravovať na výpravu. Pobalili rozličné vybavenie, ktoré by sa im mohlo zísť, ale na poslednú chvíľu si Šálka spomenul, že si zabudol v tanieri šálku, aby si mal kam naliať z termosky nevesmírny guláš. Rýchlo sa po ňu vrátil, no všimol si veľmi zvláštnu vec - Jerguša nikde nebolo. Čierna skrinka bola odkedy sa do nej spolu pozerali nedotknutá. Prezrel rôzne miestnosti, až si všimol zvláštne svetlo vzadu za haraburdami. Nachádzala sa tam zvláštna plošinka pripojená k žiariacemu kryštálu podivného tvaru, na ktorom bolo napísaných niekoľko čísel.

Zadanie

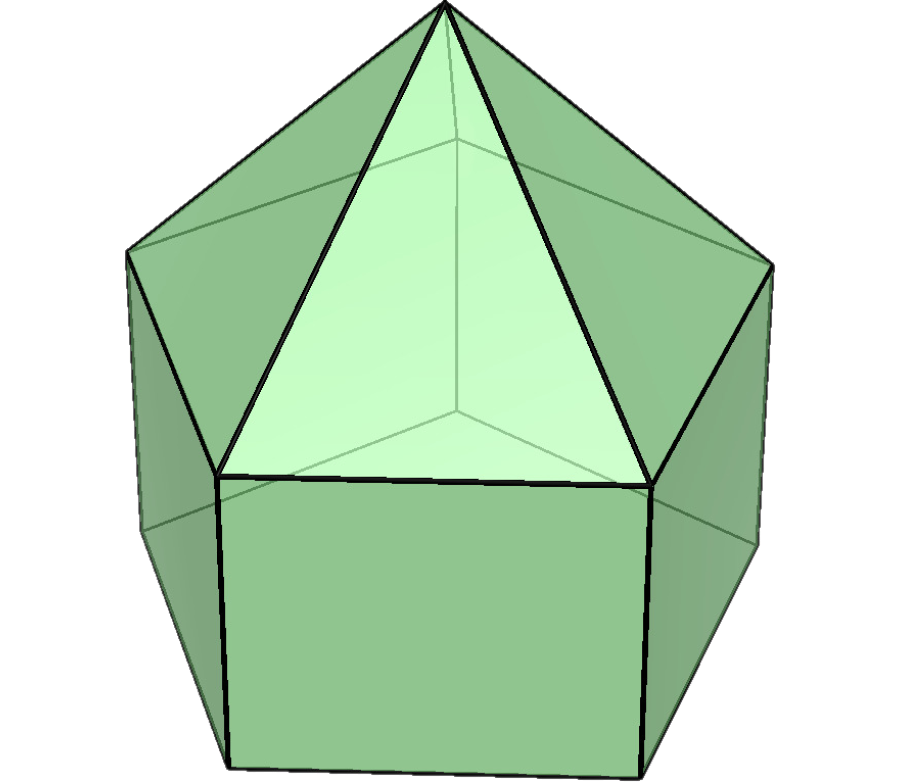
Kryštál mal tvar, ako vidíme na obrázku, teda hranol s mnohouholníkovou základňou a ihlanom s rovnakou základňou navrchu. V každom vrchole sa nachádza nejaké prirodzené číslo, pričom súčet čísel na každej stene (vrátane spodnej steny na zemi) je rovnaký. Koľko strán má základňa kryštálu, ak v niektorých jeho vrcholoch sú čísla 7, 8, 9 a 216?
Šálka sa zo zvedavosti postavil na plošinku a zmizol.
Vzorové riešenie Odovzdať

Komentáre (2)

  • Adel
    06. apríl 2020 16:37

    Môžu sa čísla opakovať? Môžu byť záporné?

  • mišo Vedúci
    06. apríl 2020 16:43

    Ahoj,
    čísla vo vrcholoch kryštálu sa môžu opakovať. Prirodzené čísla sú všetky väčšie ako 0, nemôžu byť teda záporné.

    Mišo

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa