6. príklad - Vzorové riešenie

Zo začiatku je užitočné si obrázok nakresliť:

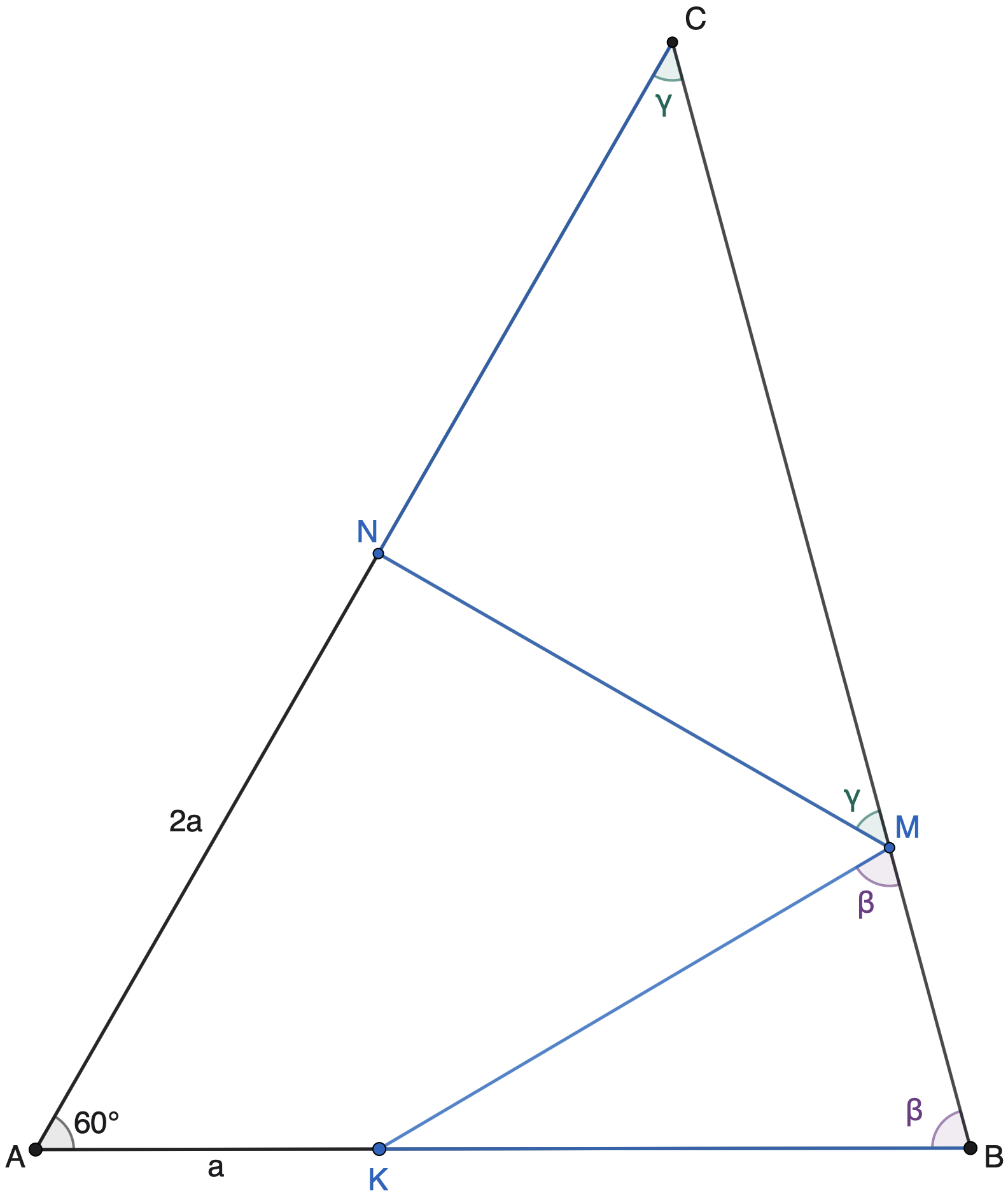
Označíme si veľkosť uhlov v trojuholníku ABC ako \left|\angle ABC \right| = \beta a \left|\angle ACB \right| = \gamma. Všimnime si, že môžeme tiež povedať \left|\angle NMC \right| = \gamma a \left|\angle KMB \right| = \beta, keďže vieme, že \left| BK\right| = \left| KM\right| a \left| MN\right| = \left| NC\right|, teda trojuholníky KBM a NMC sú rovnoramenné, a teda ich uhly pri základniach sú rovnaké.

Pozrime sa teraz na trojuholník AKN. Vieme, že \left|AK\right| je polovica z \left|AN\right|. Môžeme si teraz zvoliť taký bod X na priamke AB, ktorý je od A vzdialený rovnako ako N, alebo teda od bodu K vzdialený rovnako ako bod A, len na opačnej polpriamke. V potstate si chceme "dokresliť" trojuholník AKN na rovnoramenný.

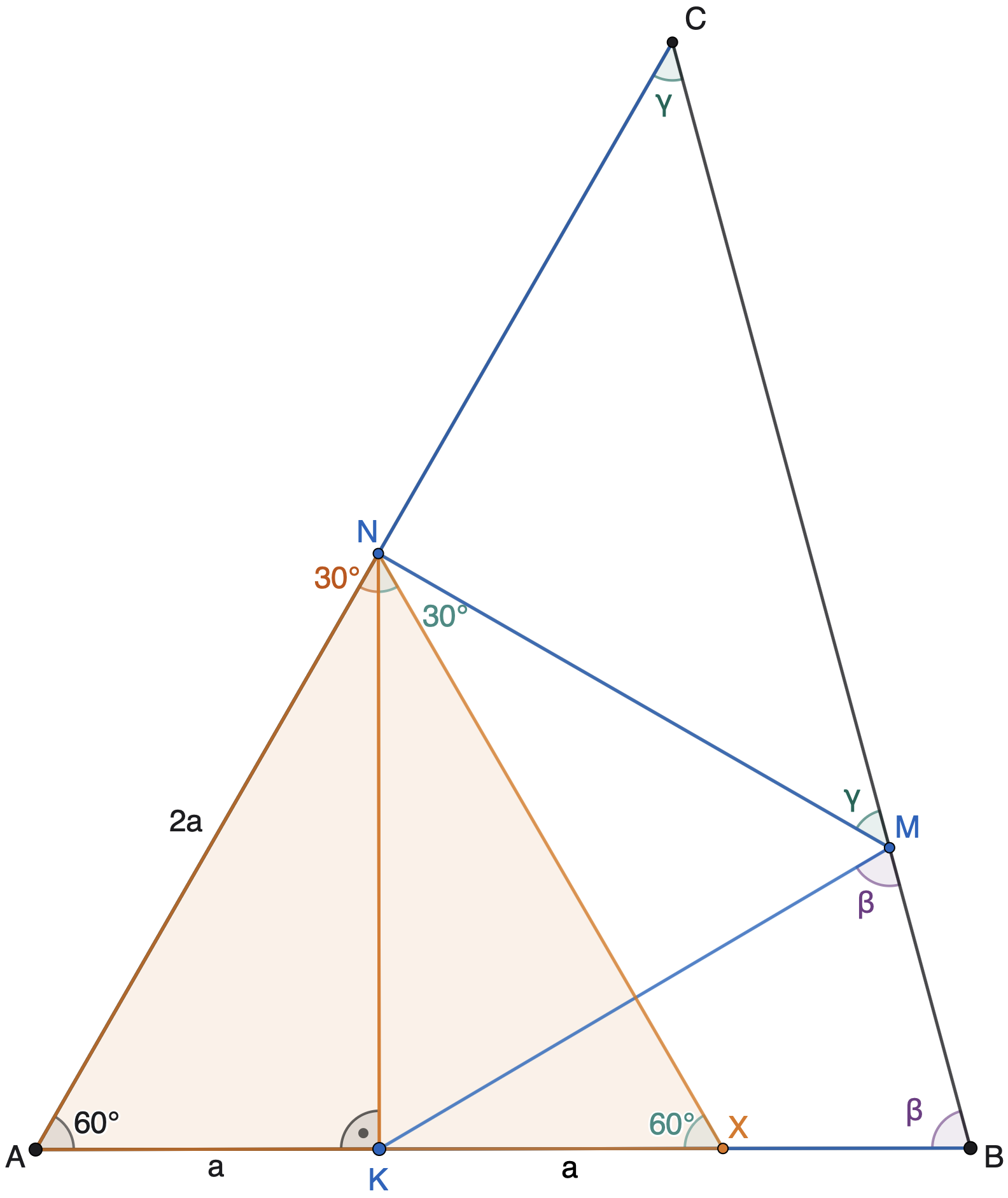
Trojuholník AXN je takto rovnoramenný, keďže \left| AX\right| = \left| AN\right|. Zo zadania však vieme, že \left|\angle BAC \right| = 60^\circ. Keď v rovnoramennom trojuholníku máme jeden uhol veľkosti 60^\circ, tak musia byť aj všetky ostatné uhly rovnakej veľkosti 60^\circ, a teda je tento trojuholník rovnostranný. Tým pádom je úsečka KN výška trojuholníku AXN na stranu AX, a teda \left|\angle AKN \right| = 90^\circ. Keďže v rovnostrannom trojuholníku každá výška delí uhol pri jej vrchole na polovicu, tak vieme, že \left|\angle ANK \right| = 30^\circ.

Teraz si poďme trochu zauhliť. Vieme už, že trojuholníky KBM a NMC sú rovnoramenné a platí, že súčet uhlov v trojholníku je 180^\circ, a teda vieme dopočítať uhly \left|\angle BKM \right| = 180^\circ - 2\beta a \left|\angle MNC \right| = 180^\circ - 2\gamma.

Všimnime si, že \left|\angle BKM \right| + \left|\angle NKM \right| + \left|\angle AKN \right| = 180^\circ, a teda keď už poznáme veľkosti uhlov \angle BKM a \angle AKN, vedeli by sme dopočítať uhol \angle NKM. Tak poďme na to! Vieme, že \left| \angle BKM \right| = 180^\circ - 2\beta a \left|\angle AKN \right| = 90^\circ, tak to môžeme dosadiť do rovnice a upravovať:

∣∠BKM∣+∣∠NKM∣+∣∠AKN∣=180^\circ

180 ^∘ −2β+∣∠NKM∣+90 ^∘ =180 ^∘

∣∠NKM∣=2β−90^\circ

Podobne si môžeme všimnúť, že ∣∠MNC∣+∣∠KNM∣+∣∠ANK∣=180^\circ, a teda vieme dopočítať uhol \angle KNM. Vieme, že \left| \angle MNC \right| = 180^\circ - 2\gamma a tiež \left| \angle ANK \right| = 30^\circ. Tak si to dosaďme do rovnice:

∣∠MNC∣+∣∠KNM∣+∣∠ANK∣=180^∘

180 ^∘ −2γ+∣∠KNM∣+30 ^∘ =180 ^∘

∣∠KNM∣+=2γ−30 ^∘

Oba tieto uhly čo sme si teraz vyjadrili sa nachádzjú v trojuholníku KMN, takže by sme sa naň mohli pozrieť trochu bližšie.

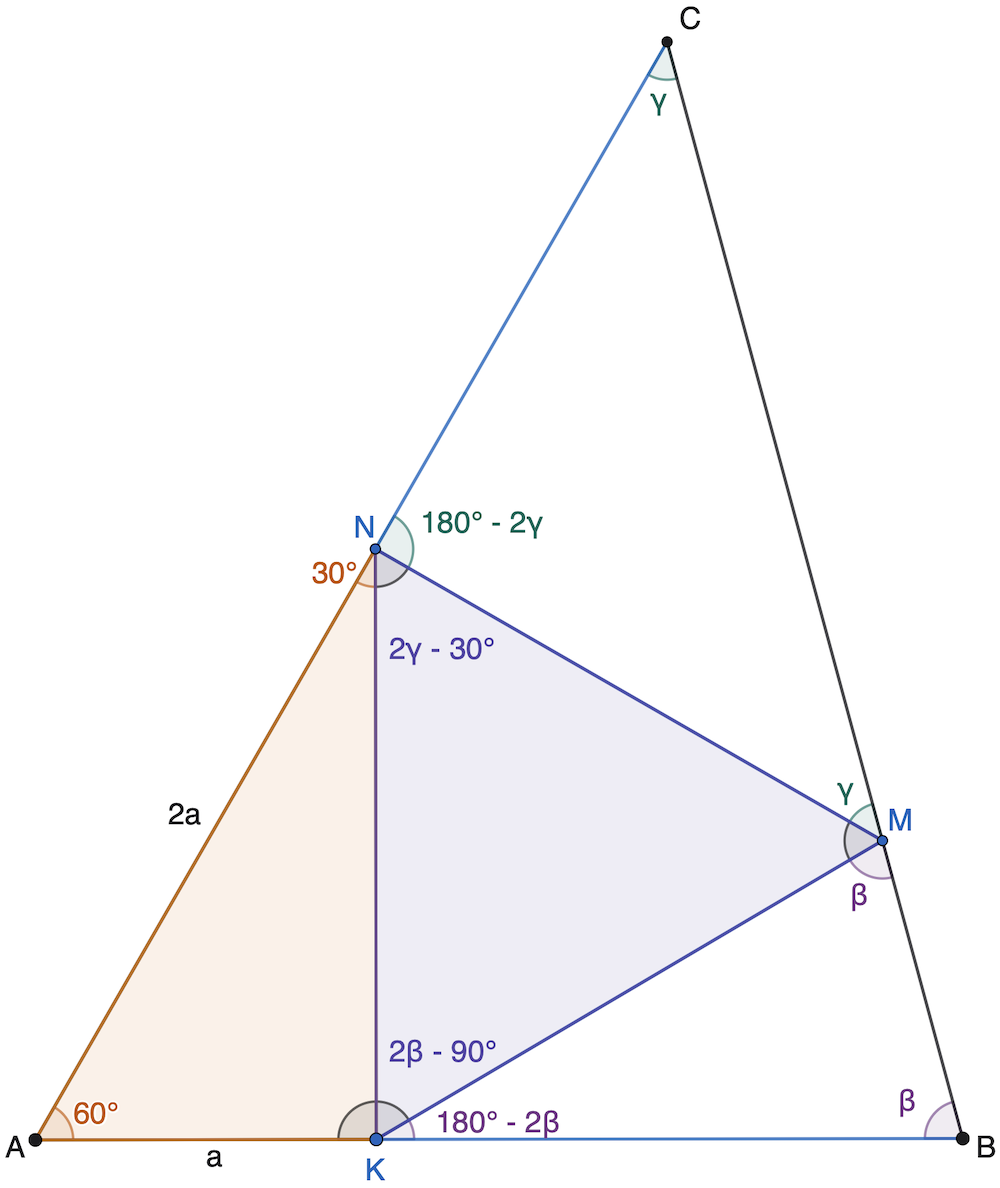
Zo zadania už vieme, že \left|KM \right| = \left| MN \right|. To znamená, že trojuholník KMN je rovnoramenný s základňou KN. Velkosti uhlov pri nej sa teda musia rovnať. Takže \left| \angle NKM \right| =\left| \angle KNM \right|. My sme však teraz vypočítali, že \left| \angle NKM \right| = 2β−90^∘ a \left| \angle KNM \right| = 2γ−30 ^∘. Teda dostávame rovnicu:

2β−90^∘=2γ−30 ^∘

Čo si vieme upraviť:

2β=2γ+60^∘β=γ+30^∘

Teraz sa vráťme späť k trojuholníku ABC. Všetky uhly v ňom majú dávať dokopy 180^\circ, teda:

60^\circ + \beta + \gamma = 180^\circ

My však vieme, že β=γ+30^\circ, čo vieme dosadiť do tejto rovnice:

60^\circ + \gamma + 30^\circ + \gamma = 180^\circ

2\gamma = 90^\circ

\gamma = 45^\circ

Takže sme zistili \left| \angle ACB \right| = 45^\circ. Teraz iba dopočítame:\left| \angle ABC \right| = 180^\circ - 60^\circ - 45^\circ = 75^\circ

Odpoveď: Veľkosť uhlu \angle ABC je 75^\circ a veľkosť uhlu \angle ACB je 45^\circ