Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×7. príklad - Vzorové riešenie
Zadanie
Studňa mala tvar obdĺžnika ABCD. Na stranách CD a BC vyznačme body X a Y také, že platí |\angle AXD| = |\angle CXY| = 45^\circ. Označme stred úsečky AX ako W a veďme ním priamku p rovnobežnú s XY. Tá pretne úsečku AB v bode Z. Nakoniec veďme bodom Y priamku q rovnobežnú s AB a označme jej priesečník s AD ako V. Ak platí |WZ| = |XY|, určte pomer obsahov obdĺžnikov ABCD a VYCD.
Vzorové riešenie
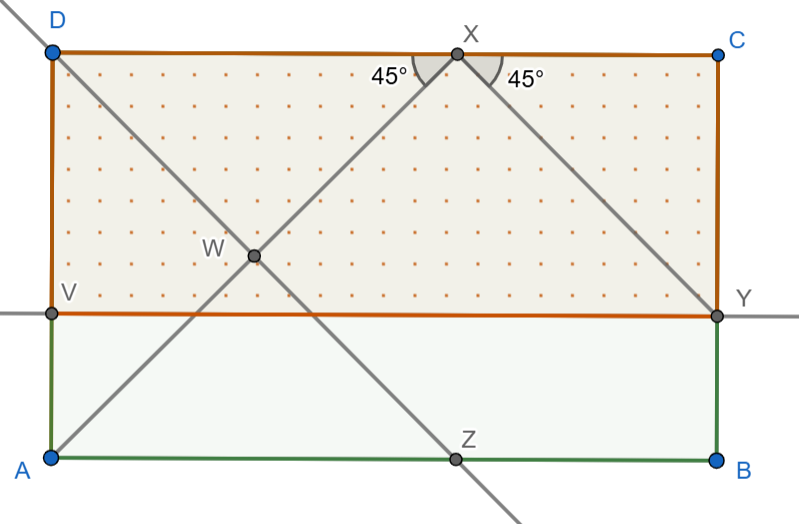
Vieme, že ABCD je obdĺžnik a teda všetky uhly má pravé. Týmito pravými uhlami sú aj ∡BCD a ∡CDA. To sú zároveň aj uhly trojuholníkov ΔYCX a ΔADX, ktoré sú teda pravouhlé. Zo zadania poznáme ešte jeden ich uhol, a to ∡AXD, respektíve ∡CXY, ktoré majú 45°. Vieme si dopočítať tretí - posledný uhol trojuholníkov - keďže vieme, že súčet vnútorných uhlov v trojuholníku je 180°. ∡XYC a ∡DAX majú teda 180°-90°-45°=45°. Trojuholníky majú dva rovnaké 45-stupňové uhly a preto sú rovnoramenné. Môžeme si dĺžky ich ramien označiť ako a a b.
∡AXY tvorí spolu s ∡AXD a ∡CXY 180°, keďže sú na jednej priamke, čiže ∡AXY=180°-90°-45°=90°. Zo zadania vieme, že úsečky \overlinesegment{XY} a \overlinesegment{WZ} sú rovnobežné, čiže uhly medzi nimi a úsečkou \overlinesegment{AX} sú súhlasné, a teda zhodné. Keďže už vieme ∡AXY (90°), vieme že ∡AWZ je tiež 90°.
Keďže ∡DAX=45°, tak ∡XAB bude 90°-45°=45°. ∡WAZ má teda 180°-90°-45°=45°. Vidíme, že aj ΔWAZ je rovnoramenný.
\overlinesegment{AX} je preponou pravouhlého trojuholníka ΔAXD. Vieme si označiť jej veľkosť ako c. Úsečku \overlinesegment{AX} delí bod W na dve polovice a \overlinesegment{AW}=\overlinesegment{WX}=\cfrac{\overlinesegment{AX}}{2}=\cfrac{c}{2}. Nakoľko vieme, že ΔWAZ je rovnoramenný, vieme že aj \overlinesegment{WZ}=c/2. Zo zadania vieme, že \overlinesegment{WZ}=\overlinesegment{XY}, čiže aj \overlinesegment{XY}=\cfrac{c}{2}.
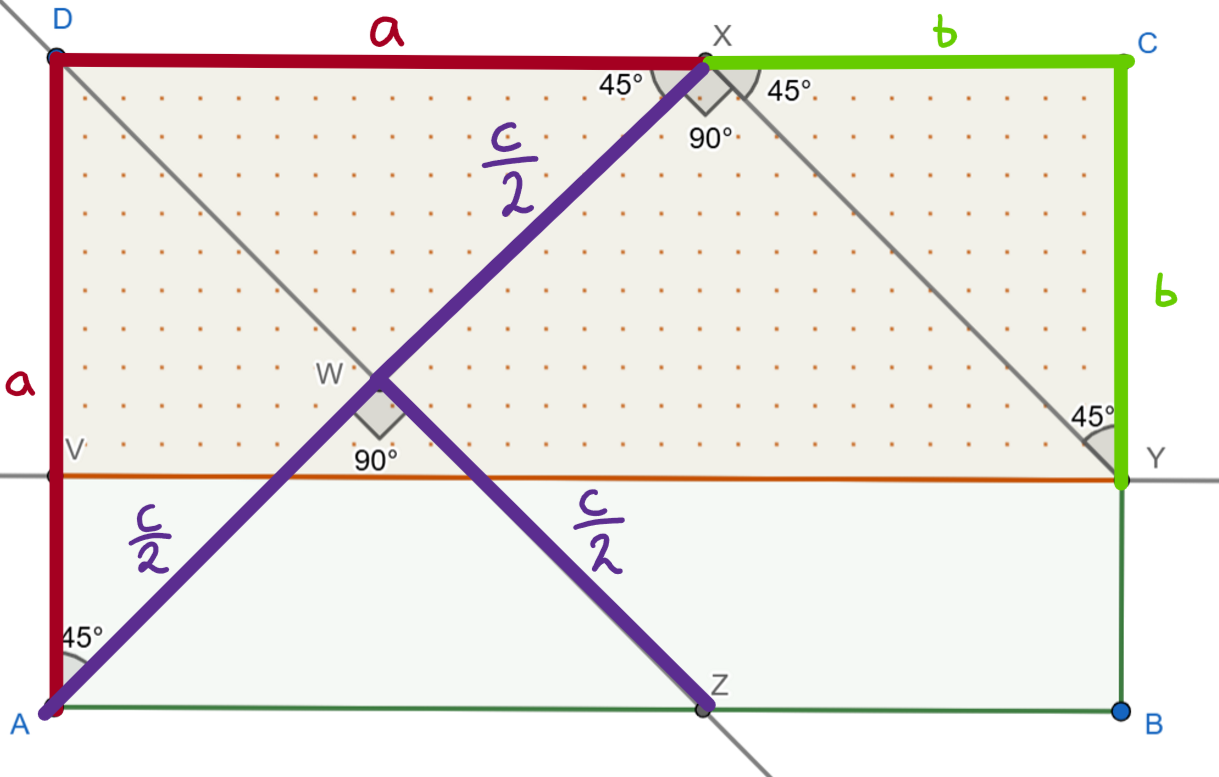
\overlinesegment{XY} je preponou pravouhlého trojuholníka ΔCXY, ktorý je podľa vety uuu podobný Δ DAX (oba trojuholníky majú všetky uhly rovnaké). Nakoľko vieme, že prepona ΔDAX, \overlinesegment{AX}, je c a prepona
ΔCXY, \overlinesegment{XY}, je \cfrac{c}{2}, vieme, že koeficient podobnosti týchto trojuholníkov je 2. To znamená, že
ΔCXY bude mať všetky strany polovičné v porovnaní s ΔDAX. To znamená, že \cfrac{a}{2}=b, respektíve a=2b.
Ako je aj z náčrtu vidieť, obsah obdĺžnika ABCD si vieme zapísať ako a×(a+b) a obsah obdĺžnika VYCD ako b×(a+b). Keď si nahradíme za všetky a hodnotu 2b, zistíme, že pomer obsahov trojuholníkov je
S_{ABCD} : S_{VYCD} = 2b×(2b+b) : b×(2b+b) = 6b^2 : 3b^2 = 6 : 3 = 2 : 1.
Obsah ABCD je dvakrát vačší ako obsah VYCD.
Obrázky sú len ilustračné a nemusia nutne spĺňať všetky podmienky zadania.
Komentár
Veľa riešiteľov si nakreslilo obrázok tak, že priamo z neho vizeralo, že body V,W a Y ležia na jednej priamke. Nanešťastie zadanie hovorí iba to, že úsečka VY je rovnobežná so stranou AB. To, že na úsečke VY leží aj bod W bolo treba dokázať. Riešeniam, ktoré použili, že body V,W a Y sú na jednej priamke sme dávali maximálne 3 body, keďže s touto vedomosťou sa dalo už jednoducho ukázať, že pomer obsahov je 1:2. Skutočne bod W je stred úsečky AX, takže ak ním vedia úsečka VY, tak už rozdeluje obdĺžnik ABCD na polovice.
