Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×1. príklad - Vzorové riešenie
Zadanie
Pod strechu dobehli Kai, Majko, Sebik, Prutky a Zuzka Š. Podľa toho, koľkí v poradí dobehli, si pripísali poradové číslo od 1 do 5. Zároveň na nich padlo počas behu 3, 3, 6, 7 a 8 kvapiek dažďa (na každého jedno z daných čísel). Spolu má teda každý poradové číslo podľa toho, koľký dobehol a kvapkové číslo podľa počtu kvapiek, ktoré naňho padli. Vieme, že:
- Súčet kvapkových čísel ľudí, ktorí prišli skôr ako Sebik, je menej ako 7.
- Majko, Sebik a Prutky majú nepárny súčin kvapkových čísel.
- Prvá prišla Zuzka Š. alebo Kai.
- Súčin kvapkových čísel tretieho a štvrtého človeka je 56.
- Prutky ako jediný prišiel medzi Zuzkou Š. a Majkom.
Zistite, v akom poradí dobehli a kto mal aké kvapkové číslo.
Vzorové riešenie
V zadaní nám bolo naraz daných pomerne veľa informácii. Dôležité je si v nich spraviť poriadok.
To, čo zistíme si budeme prehľadne spisovať napríklad do takejto tabuľky:
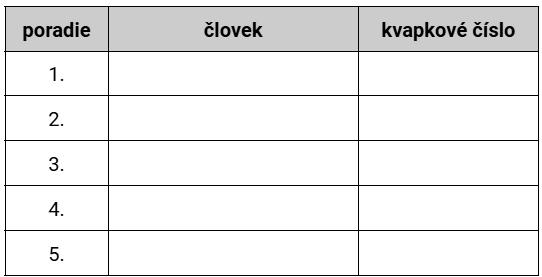
Začneme treťou podmienkou (Prvá prišla Zuzka Š. alebo Kai.). Na prvom mieste máme teda dve možnosti, Zuzka Š. a Kai. V tabuľke v tomto prípade použijeme slovíčko “alebo”.
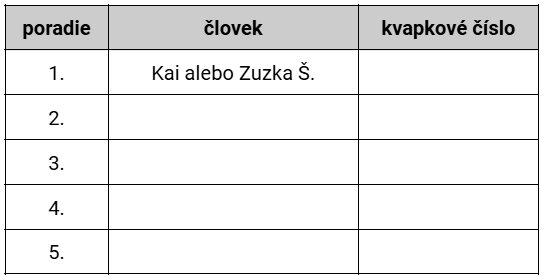
Pokračovať budeme štvrtou podmienkou (Súčin kvapkových čísel tretieho a štvrtého človeka je 56.). Vieme, že 7\cdot8=56. 7 je prvočíslo a 8=2\cdot2\cdot2, ale my 2 medzi kvapkovými číslami nemáme. To znamená, že na tretej a štvrtej pozícii musia byť práve čísla 7 a 8. Keďže máme opäť viac možností, použijeme “alebo” a jednotlivé možnosti si vyfarbíme.
Ak na treťom mieste bude 7, na štvrtom bude automaticky 8 (modrá možnosť). Ak bude na treťom 8, na štvrtom musí byť 7 (červená možnosť).
Tabuľka teda vyzerá takto:
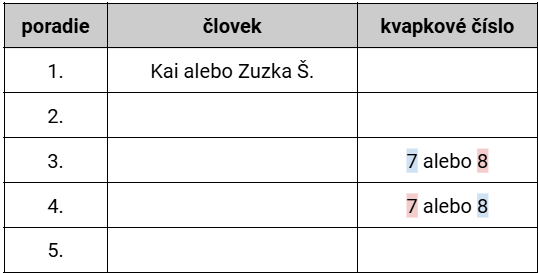
Poďme sa teraz pozrieť na prvú podmienku (Súčet kvapkových čísel ľudí, ktorí prišli skôr ako Sebik, je menej ako 7.). Pred Sebikom, teda nemôže byť vedúci, ktoré má kvapkové číslo 7 alebo 8. To znamená, že Sebik musí byť aspoň tretí (aby mohli byť vedúci s týmito číslami za ním). Ak by pred ním bol vedúci s kvapkovým číslom 6, nemohol by byť pred Sebikom nikto iný, iba tento vedúci (zelená možnosť). Ešte vedia byť pred Sebikom vedúci s kvapkovým číslom 3, buď jeden (žltá možnosť), alebo dvaja (fialová možnosť), stále bude podmienka splnená. Zapíšeme si to, pričom rôzne scenáre opäť farebne odlíšime, ako uvádzame v zátvorkách:
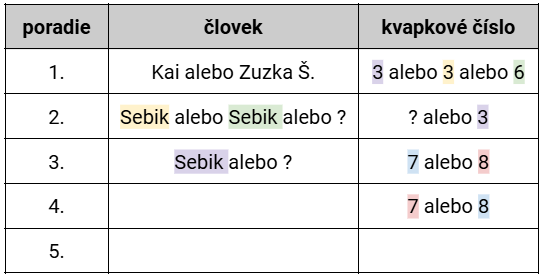
Teraz sa pozrieme na piatu podmienku (Prutky ako jediný prišiel medzi Zuzkou Š. a Majkom.). Ak by bola Zuzka Š. prvá, potom by druhý musel byť Prutky a tretí Majko. Takže Sebikovi by nezostalo miesto. To znamená, že prvý bude Kai:
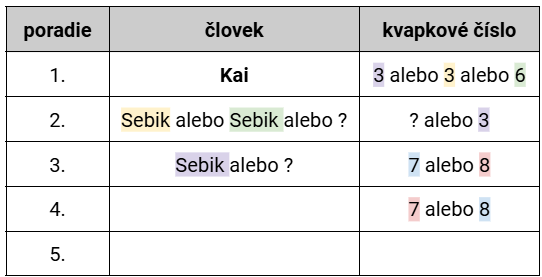
Vieme, že Zuzka Š., Prutky a Majko prišli tesne za sebou v nejakom poradí. Ak by Sebik bol tretí, nemáme tri neobsadené po sebe idúce miesta. Sebik teda bude druhý a títo traja budú na treťom, štvrtom a piatom mieste. Prutky bude uprostred (je medzi Majkom a Zuzkou Š.), čiže na štvrtom mieste. Pre Zuzku Š. a Majka máme dve alternatívy (oranžovú a fialovú).
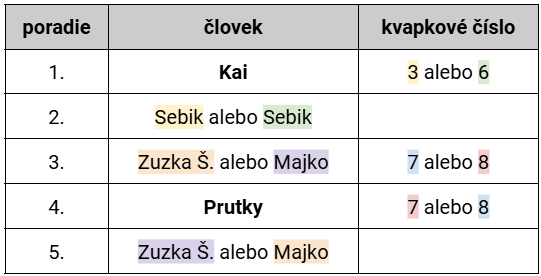
Zostala druhá podmienka (Majko, Sebik a Prutky majú nepárny súčin kvapkových čísel.). Hovorí sa tam o nepárnom súčine kvapkových čísel. Ako taký súčin docieliť? Tu si treba uvedomiť, že nepárny súčin nesmie obsahovať ani jedno párne číslo. To znamená, že Majko, Sebik a Prutky musia mať len nepárne kvapkové čísla. Keďže takéto čísla sú práve tri, vieme, že Majko, Sebik a Prutky budú mať v nejakom (zatiaľ neznámom) poradí kvapkové čísla 3, 3, a 7. Zuzke Š. a Kaiovi teda zostanú čísla 6 a 8.
Ak sa pozrieme do tabuľky, pri Prutkym máme na výber buď 7 alebo 8. Dáme mu teda číslo 7. To znamená, že pre Majka a Sebika zostali čísla 3. Zároveň to znamená, že vedúci na treťom mieste má číslo 8. Bude to teda Zuzka Š., keďže Majko má mať 3.
Pri Kaiovi máme na výber 3 alebo 6, dostane teda 6 (čo je číslo, ktoré aj zostalo, takže všetko vychádza).
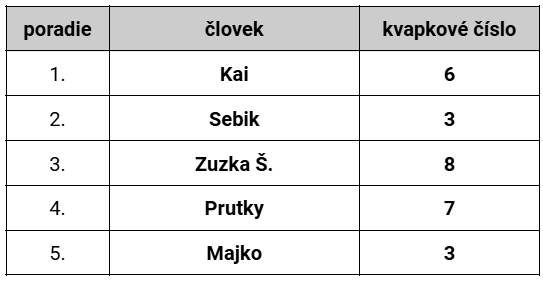
Možno ste si pri čítaní vzorového riešenia kládli jednu z týchto otázok:
- Prečo sme tie podmienky rozoberali práve v tomto poradí?
- Odkiaľ som mal/-a vedieť, že si potrebujem spraviť práve takúto tabuľku? Prečo sme priraďovali mená a kvapkové čísla k poradiu? Nemohli sme poradie a kvapkové čísla priraďovať k menám? Alebo poradie a mená priraďovať ku kvapkovým číslam?
Nuž, ani na poradí, ani na tabuľke nezáleží. Riešenie vyjde vždy rovnaké. Môžete si skúsiť sami ako cvičenie rozobrať podmienky v inom poradí a s inými tabuľkami a overiť si to 🙂.
My sme vo vzorovom riešení zvolili túto tabuľku a takéto poradie, keďže nám to prišlo najjednoduchšie na pochopenie.
