Vzorové riešenia 2. kola

Pri úlohách, kde máme namiesto cifier písmenká, je užitočné, ak si najprv dosadíme pár ľubovoľných čísel a skúsime sa s týmto príkladom trošku pohrať. Napríklad, ak si úplne náhodne povieme, že:

A=4 \\ B=5 \\ C=7 \\ D=8 \\ E=9 \\ F=2 \\ G=3 \\

\begin{array}{ccccc} & 4 & 5 & 7 & 8 & 4 \\ & - & 9 & 2 & 3 & 2\\ \hline & & 2 & 5 & 3 & 9 \end{array}

Ak takýchto náhodných dosadení (tak sa tomu hovorí, keď zamieňam cifry za písmenká) vyskúšame viac, všimneme si jednu zaujímavú vec. Okrem toho, že nám výsledok nesedí číselne, nám nesedí ani počet cifier výsledku. Ak od päťciferného čísla odpočítavame štvorciferné, je pomerne náročné získať štvorciferný výsledok. To znamená, že chceme pravdepodobne skúšať odpočítavať veľké štvorciferné čísla od malých päťciferných. Dokonca musí byť toto päťciferné číslo menšie ako 20000. Pretože, aj kebyže si zoberieme najväčšie štvorciferné číslo 9999 a odpočítame ho od 20000, stále nebudeme mať štvorciferný výsledok:

\begin{array}{ccccc} & 2 & 0 & 0 & 0 & 0 \\ & - & 9 & 9 & 9 & 9\\ \hline & 1 & 0 & 0 & 0 & 1 \end{array}

Z toho dostávame prvú dôležitú podmienku, a to, že A=1.

Poďme sa teraz zamerať na miesto jednotiek. Vidíme, že musí nutne platiť jedna z dvoch možností:

E+F=1 \\ E+F=11 \\

Ak by platila prvá možnosť, aspoň jedno z čísel E, F by muselo byť 1. To sa stať nemôže, keďže cifry A, E, F musia byť podľa zadania navzájom rôzne. Takže bude určite platiť: E+F=11.

Lenže ak sa pozrieme na miesto tisícok, dostávame tam opäť tie isté písmenká E, F, lenže ich sčítaním tentokrát potrebujeme získať cifru B. (Keďže sčítanie je opakom odčítania, ktoré máme v príklade.) Ako toto dosiahnuť tak, aby cifry A a B boli rôzne? Napadá vám niečo, čo by nám vedelo nejako pomôcť? Jasné, prechod cez desiatku! Z odčítania C-F=B nám musí jedna zostať a túto jednu potom pripočítame k cifre E. To znamená, že cifra B musí byť o 1 väčšia ako cifra A, a teda B=2.

Ešte potrebujeme, aby nám naozaj jedna zostala z toho predošlého odčítania. Takže musí platiť: 10+C=2+F. Z toho je očividné, že C musí byť naozaj malé a F musí byť naozaj veľké. Lenže C už nemôže byť ani 1 a ani 2, keďže C musí byť rôzne od A aj B. Ak by C bolo 3 a viac, F by už muselo byť väčšie ako 9. Z toho vyplýva, že C=0. A teda F môže byť buď 7 alebo 8, podľa toho, či nám jedna zostane z predošlého odčítavania. Ak pospomíname, o čom sa písalo kúsok vyššie, spomenieme si, že o cifrách E a F vieme, že ich súčet musí byť 11. Takže ak F môže byť len 7 alebo 8, potom E môže byť len 4 alebo 3.

Teraz sa pozrime na miesto desiatok. Vieme, že nám z predošlého odčítania jedna zostane, takže bude platiť jedna z dvoch možností, keďže nám pokojne môže aj jedna zostať:

G+G+1=D \\ G+G+1=10+D \\

Pozrime sa najprv na prípad, že by bola správna prvá rovnica G+G+1=D. Znamenalo by to, že potrebujeme malé G a veľké D. Keďže cifry 0, 1, 2 už sú obsadené inými písmenkami a cifra 5 je pre G priveľká, dostávame pre G a D práve dve možnosti:

G=3 \\ D=7 \\

G=4 \\ D=9 \\

V tomto prípade nám však nič nezostane do ďalšieho odčítania, takže potrebujeme, aby F=8, a teda E=3, keďže E+F=11. Takže ak nechceme, aby sa nám opakovali cifry, musí automaticky platiť G=4 a D=9.

Teraz sa pozrime na druhý prípad, a to, že je správna druhá rovnica G+G+1=10+D. V tomto prípade musí byť F=7 a E=4, keďže jedna zostane. Pre cifry D a G teda zostávajú možnosti 3, 5, 6, 8, 9. Poďme vyskúšať všetky možné D:

D=3 \\ 3+3+1 = 7 \\ D=5 \\ 5+5+1 = 11 \\ D=6 \\ 6+6+1 = 13 \\ D=8 \\ 8+8+1 = 17 \\ D=9 \\ 9+9+1 = 19 \\

Z toho nám vyjde, že jediný prípad, kedy sa nabudú opakovať žiadne cifry je 6+6+1=13, kde D=6 a G=3.

Odpoveď: Existujú dve možnosti, ako prideliť cifrám zo zadania hodnotu.

Prvá vyzerá takto:

\begin{array}{ccccc} & 1 & 2 & 0 & 9 & 1 \\ & - & 3 & 8 & 4 & 8\\ \hline & & 8 & 2 & 4 & 3 \end{array}

Druhá takto:

\begin{array}{ccccc} & 1 & 2 & 0 & 3 & 1 \\ & - & 4 & 7 & 6 & 7\\ \hline & & 7 & 2 & 6 & 4 \end{array}

Komentár

V prvom rade je veľmi praktické si veci označovať skratkami, takže ak sa bude v tomto vzorovom riešení za číslom nachádzať z, tak budeme hovoriť o počte zelených kociek a ak tam bude s, tak budeme hovoriť o počte sivých kociek.

Vidíme, že je v zadaní celkom veľa podmienok a môže byť náročné sa v nich všetkých hneď orientovať a uvedomovať si ich. Preto je užitočné nezačať so všetkými ale vybrať si pár, od ktorých sa potom budeme vedieť ďalej odraziť. Začnime teda s prvými dvoma podmienkami o deliteľnostiach počtov kociek. Poďme si skúsiť vypísať všetky možnosti rozloženia kociek tak, že zelené sú násobok 6. Následne k tomu doplníme počet sivých kociek tak, aby bol celkový počet kociek 54.

0z + 54s \\6z + 48s \\12z + 42s \\18z + 36s \\24z + 30s \\30z + 24s \\36z + 18s \\42z + 12s \\48z + 6s \\54z + 0s \\

Lenže vieme, že počet sivých kociek musí byť deliteľný štvorkou, a teda z možností vypísaných vyššie prichádzajú do úvahy len tieto:

6z + 48s \\18z + 36s \\ 30z + 24s \\42z + 12s \\54z + 0s \\

V tomto bode sme už využili prvé dve podmienky zo zadania najviac ako sa dalo, no stále nám zostalo celkom veľa rôznych počtov kociek, a teda aj počtov vedúcich, ktoré vieme brať do úvahy. Piata podmienka hovorí, že každý vedúci musí mať aspoň dvakrát viac sivých kociek ako zelených. To znamená, že aj dokopy musí byť aspoň dvakrát viac sivých kociek, takže prvé tri počty by nevyhovovali. Zostávajú nám tieto počty:

6z + 48s \\18z + 36s \\

Poďme sa teraz pozrieť na tretiu podmienku. Hodnota zelenej kocky má byť trikrát väčšia ako hodnota sivej kocky. Táto podmienka znamená, že hodnoty zelenej a sivej kocky môžu byť napríklad 3 a 1, ale aj 6 a 2, 9 a 3, či kľudne 300 a 100. V riešení budeme pracovať s hodnotami 3 a 1, no skúste sa zamyslieť, prečo by sme dostali rovnaký výsledok počtov vedúcich aj pre iné hodnoty kociek, ktoré spĺňajú podmienku trojnásobnej hodnoty ;).

Poďme si teda vypočítať celkové hodnoty pre tieto dva prípady počtov kociek:

6z + 48s \\6 \cdot 3 + 48 \cdot 1 = 66 \\18z + 36s \\18 \cdot 3 + 36 \cdot 1 = 90 \\

Keďže štvrtá podmienka hovorí o tom, že každý vedúci musí mať rovnakú hodnotu, znamená to, že počet vedúcich musí deliť celkovú hodnotu. Vypíšme si teda delitele čísel 90 a 66:

66 = 1 \cdot 66 \\66 = 2 \cdot 33 \\66 = 3 \cdot 22 \\66 = 6 \cdot 11 \\66 = 11 \cdot 6 \\

90 = 1 \cdot 90 \\90 = 2 \cdot 45 \\90 = 3 \cdot 30 \\90 = 5 \cdot 18 \\90 = 6 \cdot 15 \\90 = 9 \cdot 10 \\

Teraz prichádza na rad posledná podmienka, a to, že každý vedúci dostal minimálne jednu zelenú kocku. To znamená, že v prvom prípade musí byť počet vedúcich najviac 6 a v druhom najviac 18. Z toho dostávame nasledovné počty vedúcich: 1, 2, 3, 5, 6, 9, 10, 15 a 18. Poďme teda vyskúšať, ktoré z týchto počtov vedúcich vedia byť výsledkom. Počet vedúcich vie byť výsledkom v momente, ak sa vedia kocky medzi vedúcich rozdeliť tak, že budú platiť všetky podmienky zo zadania. Najprv to predvedieme len na počtoch vedúcich, ktoré fungujú, a teda 1, 2, 3, 6, 9 a 18. Pre 5, 10 a 15 to fungovať nebude, nižšie vysvetlíme, že prečo.

V tabuľke vždy uvedieme zelené a sivé kocky, ktoré má jeden vedúci. Toto urobíme pre každý počet veducich a pre obe rozloženia kociek - 6 zelených a 48 sivých a aj pre 18 zelených a 36 sivých.

Poďme sa teraz pozrieť na hodnoty 5, 10 a 15. Pripomeňme si, že tieto počty vedúcich môžeme uvažovať len pre rozdelenie 18 zelených a 36 sivých, a teda hodnotu 90.

Začnime s 5. V tomto prípade je isté, že aspoň jeden vedúci bude mať 4 zelené kocky, keďže ak dáme každému 3, tak nám ešte 3 zostanú. V takom prípade potrebuje aspoň 8 sivých kociek, aby platila piata podmienka. Takto majú kocky vedúceho spolu hodnotu:

3 \cdot 4 + 1 \cdot 8 = 20

Lenže ak je celková hodnota 90, počet vedúcich 5 a chceme aby mal každý vedúci rovnakú hodnotu (štvrtá podmienka), musí platiť, že táto hotnota je: 90 \div 5 = 18, čo je menej ako 20.

Také isté odôvodnenie dostávame aj pre počet vedúcich 10. V tomto prípade má nejaký vedúci aspoň 2 zelené kocky, a teda 4 sivé kocky čo má spolu hodnotu:

2 \cdot 3 + 4 \cdot 1 = 10

Lenže hodnota každého vedúceho musí byť práve:

90 \div 10 = 9

Pre počet vedúcich 15 to vyjde rovnako, akurát žiadaná hodnota bude:

90 \div 15 = 6

Z toho teda vyplýva, že počet vedúcich nevie byť 5, 10 a 15.

Odpoveď: Vyhovujúce počty vedúcich sú: 1, 2, 3, 6, 9 a 18

Aby Ivka zjedla čerešňovú buchtu najneskôr ako štvrtú, musí mať už po tretej zjedenej istotu, ktorá zo zvyšných to je (ak na ňu dovtedy náhodou nenatrafila). Po zvyšok riešenia budeme predpokladať, že sa Ivke nepodarí zjesť čerešňovú buchtu skôr štvrtú v poradí.

O buchtách vieme, že sú v poradí: 7​ kapustových, 7​ mäsových, 1​ čerešňová. To znamená, že v smere, v ktorom Ivka vykladala buchty (povedzme, že to bolo doprava, takže v smere hodinových ručičiek), je od čerešňovej buchty 7​ kapustových a v opačnom 7​ mäsových. Takže smerom doprava je medzi čerešňovou a každou mäsovou buchtou aspoň 7​ kapustových (a možno ešte ďalšie mäsové) a naopak medzi čerešňovou a každou kapustovou buchtou je v opačnom smere aspoň 7​ mäsových (a možno ešte ďalšie kapustové).

Zoberme teda prvú buchtu ľubovoľne. Ak je kapustová, vieme, že aspoň ďalších 7​ buchiet napravo od nej nie je čerešňová (lebo najmenej musíme preskočiť všetkých 7​ mäsových), takže ich už ani nemusíme skúšať. To isté, iba v opačnom smere, platí, ak je prvá buchta mäsová.

Zostalo 7​ po sebe idúcich buchiet, ktoré môžu byť tá čerešňová. Naľavo od čerešňovej sú všetky mäsové, ktoré sme ešte nevylúčili, a napravo všetky také kapustové. Z týchto si vyberieme prostrednú: ak je kapustová, vieme, že čerešňová je v jednej z troch vľavo od nej, lebo čerešňová je vľavo od každej kapustovej buchty. Ak je mäsová, platí to isté, ale čerešňová buchta je určite vpravo.

Toto isté zopakujeme ešte raz s poslednými tromi buchtami, ktoré sme nevylúčili. Ak je táto tretia, ktorú Ivka ochutnala mäsová, čerešňová je vpravo od nej, ak je tá buchta kapustová, čerešňová je od nej vľavo.

Pre zhrnutie. Ivka bude postupovať nasledovne. Prvú buchtu si zvolí ľubovoľne. Ak bola prvá buchta kapustová, tak si ako druhú buchtu vyberie buchtu, ktorá je o 4​ buchty proti smeru vyberania ďalej, inak si zvolí buchtu o 4​ buchty v smere vyberania ďalej. Ak bola druhá buchta kapustová, tak si ako tretiu buchtu vyberie buchtu, ktorá je o 2​ buchty proti smeru vyberania ďalej, inak si zvolí buchtu o 2​ buchty v smere vyberania ďalej. Ak bola tretia buchta kapustová, tak si ako štvrtú buchtu vyberie buchtu, ktorá je o 1​ buchtu proti smeru vyberania ďalej, inak si zvolí buchtu a 1​ v smere vyberania ďalej.

Ivka týmto postupom každou zjedenou buchtou zmenší časť kruhu, v ktorej sa čerešňová buchta môže nachádzať na polovicu, takže po 3​ buchtách bude vedieť, kde sa bude nachádzať.

Odpoveď: Ivka vie zjesť najviac 4​ buchty tak, aby jedna zo zjedených bola čerešňová.

Ak chceme mať istotu, že z aspoň jednej farby ponožiek bude párny počet, tak vlastne chceme, aby sa tento počet nedal dostať vybratím nepárneho počtu alebo nuly z každej farby. 

Môžeme si všimnúť, že pri nízkych počtoch sa párnym počtom jednoducho vyhneme, a dôležitá tam bude nula. Ak napríklad Danko vytiahne 20 ponožiek, môže mať 5 modrých, žltých, bielych a zelených, a žiadne červené, čiže nemá istotu párneho počtu. Ak by Danko chcel vytiahnuť o jednu viac, môže sa mu stať to isté, ale vytiahne k tomu ešte jednu červenú. Ak by chcel vytiahnuť 22 ponožiek, môže sa mu stať to isté čo pri 12, ale namiesto modrej vytiahne o dve viac z nejakej inej farby. Pri 23 zase vytiahne jednu modrú, a tak ďalej... 

Pri každom párnom počte je dôležité to, že z niektorej farby môže vytiahnuť 0 ponožiek. Ak by sme vedeli, že z každej vytiahol aspoň jednu, a chceme aby boli všetky počty nepárne, aj celkový výsledok bude nepárny. Súčet piatich (a ľubovoľného nepárneho počtu) nepárnych čísel je vždy nepárny.

Vyzerá to teda celkom beznádejne, kým vieme vytvoriť vyššie popísaný protipríklad. Kedy sa to už nebude dať spraviť? Jedine vtedy, keď bude Danko ťahať párny počet ponožiek, pri ktorom určite musí ťahať z každej kôpky. Aby nemal z ničoho párny počet, tak vie ťahať najviac 9 červených,
11​ bielych 13​ žltých 15 zelených a 17 modrých ponožiek. Potrebujeme teda, aby mu nestačilo ani vytiahnuť všetky ponožky zo štyroch najpočetnejších farieb. To sa stane, ak  vytiahne viac ako 17+15+13+11=56 ponožiek. Chceme aby to bolo párne číslo, čiže 58. Pri tomto počte vieme, že ak by nevytiahol zo žiadnej farby párny počet, musí vytiahnuť aspoň jednu ponožku z každej farby. Potom ale môže dosiahnuť celkový párny počet ponožiek iba tak, že z niktorej farby ponožiek bude mať párny počet.

Pre 58 ponožiek má teda istotu, že bude mať z niektorej farby párny počet. Pre ľubovoľný menší počet existuje možnosť, že vytiahne 1 červenú ponožku a nejaké nepárne počty zvyšných (ak je celkový počet ponožiek nepárny), alebo vytiahne 0 červených ponožiek a nejaké nepárne počty zvyšných. Konkrétne spôsoby vieme vytvoriť napríklad postupom popísaným vyššie.

Odpoveď: Danko musí vytiahnuť aspoň 58 ponožiek.

Nakoľko pracujeme s trojuholníkami a uhlami, bude sa nám hodiť známy fakt - v trojuholníku je súčet uhlov 180°​. 

Našim cieľom je vedieť rozdeliť akýkoľvek trojuholník na 45​ trojuholníkov. Z toho 22​ trojuholníkov má mať aspoň jeden uhol 22°​ a 23​ trojuholníkov má mať aspoň jeden uhol 23°​. Chceme teda nájsť systém, ktorým postupne docielime toto rozdelenie. 

Mnohí z vás si všimli, že každý trojuholník sa dá rozdeliť na dva pravouhlé trojuholníky - pomocou výšky. Výška padá mimo trojuholníka iba v prípade, že ide o stranu ktorá je ramenom tupého uhla. Avšak v trojuholníku vie byť najviac jeden tupý uhol a preto v každom trojuholníku sú aspoň dva ostré uhly. Tým pádom tam je určite strana, ktorá je ramenom dvoch ostrých uhlov a jej výška sa teda bude nachádzať v danom trojuholníku. Rovnako to platí aj pri pravouhlom, teda nám nerobí problém ani fakt, že v pravouhlom sú dve výšky zhodné s dvoma stranami. 

Pravý uhol sa dá rozdeliť na dva  22°​ uhly a dva 23°​ uhly, pretože 90 = 22 + 22 + 23 + 23​. Tým pádom z jedného pravouhlého trojuholníka vieme dostať až dva 22°​ trojuholníky a dva 23°​ trojuholníky. 

Našim cieľom preto bude rozdeliť ľubovoľný trojuholník na 11​ pravouhlých trojuholníkov (z toho dostaneme 22​ trojuholníkov s 22°​ a 22​ trojuholníkov s 23°​) a jeden s 23°​. 

Teraz je dôležité opísať aj postup, ako sa dostaneme ku finálnemu počtu zo zadania. 

Trojuholník vieme rozdeliť na dva pravouhlé. Potom jeden z tých pravouhlých taktiež vieme rozdeliť na dva. To znamená, že sa nám pridá jeden pravouhlý trojuholník - mali sme dva, po rodzdelení máme tri. Alebo všeobecne - mali sme n​, po rozdelení máme n+1​. Takýchto rozdelení musíme spraviť postupne 10​, čím dosiahneme 11​ pravouhlých trojuholníkov. 

Týmto dostávame všetko, čo potrebujeme, okrem toho posledného 23°​ trojuholníka. 

Tu sa vrátime na začiatok, kedy začíname pracovať s našou sieťou. Z trojuholníka rovno odkrojíme menší trojuholník s jedným uhlom 23°​. Toto určite môžeme urobiť, nakoľko aspoň jeden uhol bude určite vačší ako 23°​. To sa dá dokázať tak, že 3\cdot23=69​, čo je výrazne menej ako 180​ a teda aspoň jeden z uhlov musí mať viac ako 23°​. S trojuholníkom, ktorý nám ostal po odkrojení 23°​ trojuholníka potom pracujeme rovnako, ako sme to v riešení opisovali, keďže je to stále všeobecný trojuholník. 

Súčet všetkých deliteľov čísla n​ si označíme ako d​. Medzi deliteľov n​ bude určite patriť 1​ a samotné n​. Označme si súčet ostatných deliteľov čísla n​ ako x​.

Prepíšme si informácie zo zadania do rovnice a upravme ju:

\frac{d}{n}=1,2 \\ \frac{d}{n}=\frac{6}{5}      / \cdot n \\ d=\frac{6n}{5}

Vieme, že n​, 6n​, všetky delitele n​ a tým pádom aj d​ sú prirodzené čísla. Preto musí byť \frac{6n}{5}​ prirodzené číslo a to vieme docieliť iba tak, keď bude 5​ deliteľom 6n​. Vidíme, že 6​ nie je deliteľné 5​ a teda na to, aby 5​ delilo 6n​ musí 5​ deliť n​. Keď je n​ deliteľné číslom 5​, tak určite musí byť jeden z deliteľov n​ aj číslo 5​ aj číslo \frac{n}{5}​. 

Prejdime si najprv možnosť, kde je n​ prvočíslo (nemá iných deliteľov ako 1​ a n​). Vyššie sme si dokázali, že n​ musí byť deliteľné 5​ a jediné prvočíslo, ktoré je deliteľné číslom 5​ je 5​. Overme, či vychádza možnosť n=5​:

n=5 \\ d=1+5=6 \\ \frac{d}{n}=\frac{6}{5} \\ \frac{6}{5}=\frac{6}{5}​

n=5​ je jediné prvočíselné riešenie príkladu.

Poďme zistiť, či existuje n​, ktoré nie je prvočíslo a pre ktoré platia podmienky zo zadania. Dosaďme do pôvodnej rovnice namiesto hodnoty d​, hodnotu x+1+n​ a upravme

\frac{d}{n}=\frac{6}{5} \\ \frac{x+1+n}{n}=\frac{6}{5} \\ \frac{x+1}{n}+1=\frac{6}{5}     /-1 \\ \frac{x+1}{n}=\frac{1}{5}    / \cdot n \\ x+1=\frac{n}{5}

Dostali sme sa do sporu, pretože x​ je súčtom deliteľov čísla n​, v ktorom sa určite nachádza číslo \frac{n}{5}​ (aj číslo 5​). Preto aj keby nemalo n​ žiadnych iných deliteľov, tak už určite bude iba samotné x \gt \frac{n}{5}​ a nie rovné. 

Odpoveď: Jediné číslo, ktoré spĺňa zadanie je 5​.

Pre n = 1 máme 2 \times 2 šachovnicu. Každým ťahom vedúci iba vymenia medzi týmito dvoma stavmi:

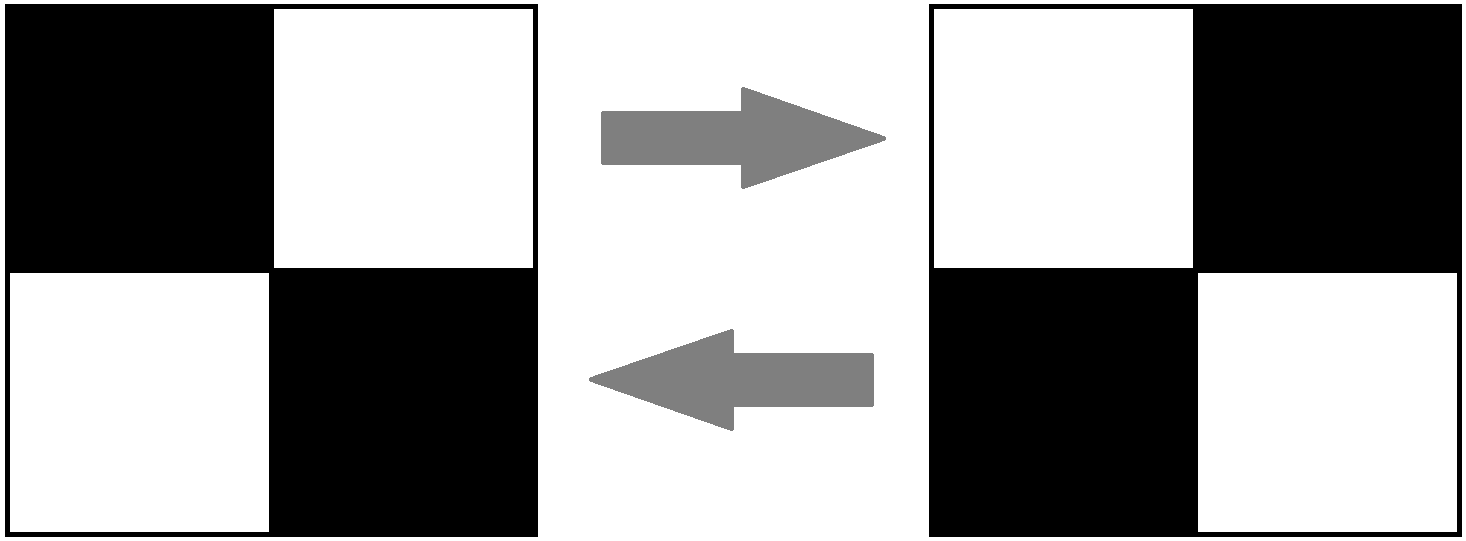
Preto sa pre n = 1 šachovnica zjednofarebniť nedá.

Keď n = 2, máme 4 \times 4 šachovnicu. Môžeme skúšať rôzne ťahy. Nie je veľmi ťažké po chvíli skúšania šachovnicu zjednofarebniť, napríklad takto:

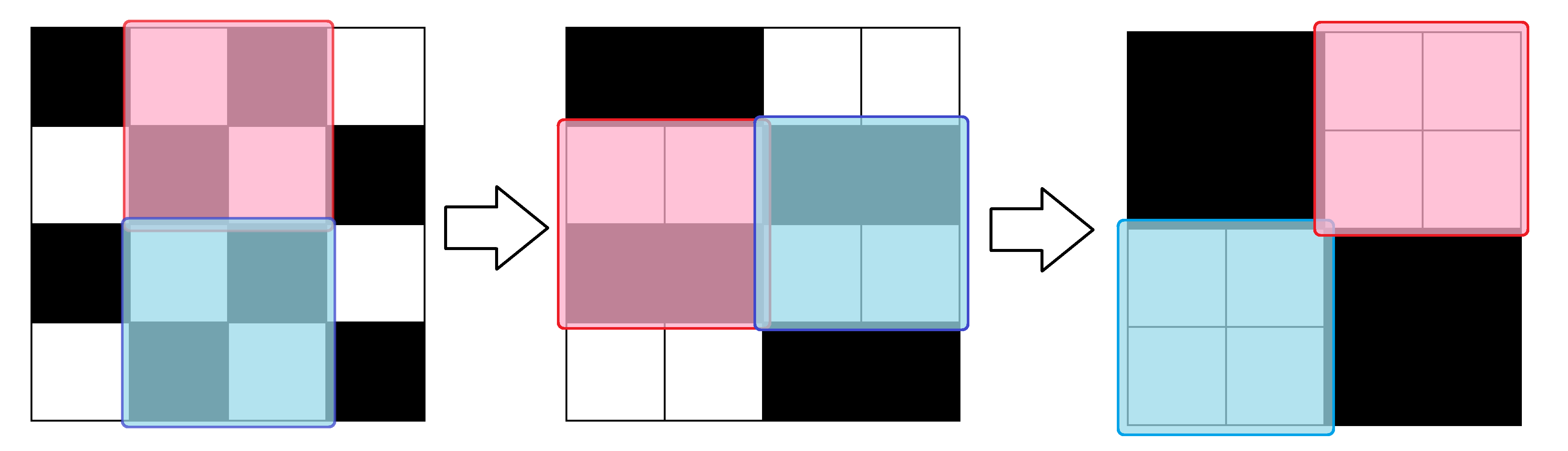
Pre n deliteľné 2​ vieme šachovnicu rozdeliť na menšie 4 \times 4 štvorce. Keď je totiž n deliteľné dvomi, tak 2n je deliteľné štyrmi. Každý z týchto štvorcov môžeme potom zjednofarebniť samostatne, čím zjednofarebníme celú šachovnicu. Pre párne n​ sa teda šachovnica dá zjednofarebniť.

Môžeme sa snažiť zjednofarebniť šachovnicu aj pre nepárne n, ale nech robíme čo robíme, nebude sa nám to dariť. Nech sa budeme snažiť ako chceme, nepodarí sa nám zjednofarebniť ani prvý riadok tabuľky. Poďme teda skúsiť dokázať, že sa to naozaj nedá.

Pri každej výmene 2 \times 2 štvorca sa v prvom riadku môžu stať štyri veci:

• Vyberieme taký štvorec, ktorý nemá v sebe nič z prvého riadku, teda nijako prvý riadok neovplyvní
• Vyberieme štvorec, ktorý má v prvom riadku jedno čierne a jedno biele políčko. Biele políčko teda zmeníme na čierne a čierne na biele, dokopy teda nezmeníme počet bielych a čiernych políčok v prvom riadku
• Vyberieme štvorec, ktorý má v prvom riadku dve biele políčka. Obe zmeníme na čierne a teda prvý riadok má o dve biele políčka menej a o dve čierne viac.
• Vyberieme štvorec, ktorý má v prvom riadku dve čierne políčka. Obe zmeníme na biele a tak sú v prvom riadku teraz o dve čierne políčka menej a o dve biele viac.

Vidíme teda, že vždy vieme premieňať čierne políčka na biele a naopak len po dvoch - buď ich počty nezmeníme, alebo ich zvýšime / znížime rovno o 2.​

Na začiatku máme v prvom riadku n bielych a n čiernych políčok. Keď je n nepárne, tak ich je nepárny počet. My ale tento počet vieme meniť vždy len o 2​. Keď pripočítavame alebo odpočítavame od nepárneho čísla 2​, dostaneme vždy len nepárne číslo, teda vždy budeme mať nepárny počet čiernych a nepárny počet bielych políčok v prvom riadku.

Na konci by sme chceli mať 0 políčok jednej farby a 2n tej druhej. To sú ale obe párne čísla, takže ich iba pripočítavaním a odpočítavaním 2​ nevieme dosiahnuť.

Odpoveď:

Pre párne n sa šachovnica zjednofarebniť dá, pre nepárne sa nedá.

Najprv si dokážme jedno pomocné tvrdenie.

Prvé pomocné tvrdenie: žiadny zo sčítancov v príklade nie je nula. Toto vieme ľahko dokázať tak, že vieme, že všetky premenné (čísla a,b,c,d,e​) sú aspoň jedna. Potom keď sa pozrieme na najmenší člen, tak vo výraze \frac{e+d}{3} je aj d​, aj e​, aspoň jedna, a keďže d​ musí byť od e​ ostro väčšie, celý výraz bude mať hodnotu aspoň \frac{1+2}{3} = 1.

Druhé pomocné tvrdenie: nemôžeme mať viac ako dva rovnaké sčítance. Prečo? Pozrime sa na čitatele tri po sebe idúcich výrazov, a najmenšie možné čísla, aké v nich môžu byť:
x+(x+1)=2x+1
(x+1)+(x+2) = 2x +3
(x+2)+(x+3)= 2x+5
Vidíme, že prvý člen bude v čitateli aspoň o 4​ väčší ako tretí, a teda nemôžu mať po vydelení troma a zaokrúhlení na najbližšie celé číslo rovnakú hodnotu.

Dobre, tak sa vrhnime na rovnicu. Vidíme, že sčítavame druhé mocniny celých čísel. Tých nie je veľa, najmä čo sa týka takých, ktoré sú menšie ako 38​. Je ich len 6: 1, 4,9,16,25,36​. 36​ Dokonca môžeme hneď vylúčiť, pretože 38 - 36 = 2​, a ako vieme, zvyšný súčet 2 musíme dostať pomocou troch nenulových celých sčítancov, čo nie je možné. Teda náš zoznam možných sčítancov vyzerá asi takto: 1,4,9,16,25.​​

Môžeme si všimnúť, že sčítať musíme aspoň jednu 16​ alebo 25​, pretože 4\cdot9 = 36​, čo je stále menšie ako  38​. Zároveň nemôžeme mať ako sčítanec obe, pretože 16+25 = 41​, čo je viac ako 38​. 

Môžeme mať v súčte dve 16​? Poďme sa na to pozrieť. Máme teda sčítance 16+16=32​, a teda ostáva nám pomocou dvoch zvyšných čitateľov dostať súčet 6​. Rýchlo však zistíme, že keďže z čísel menších ako 6​ máme v zozname povolených sčítancov iba 4​ a 1​, tak to nie je možné. Musíme totiž sčítať práve dve čísla. Teda sme dokázali, že číslo 16​ sa ako sčítanec dvakrát nevyskytne.

Dobre, teda vieme, že budeme mať práve jedno z čísel 16​ a 25​ ako sčítanec. Čo keby sme teda mali 25​? Musíme teda sčítať súčet 38-25=13​ pomocou troch sčítancov. Možnosti máme iba 1,4,9​. Jedna deviatka v tomto súčte byť musí, lebo 3\cdot4=12​ čo nestačí. Teda 13-9=4​. Máme vyskladať súčet 4​ pomcou práve dvoch sčítancov, ktorú sú buď 1​ alebo 4​, čo opäť nejde. Teda 25  nemôže byť ako sčítanec.

Jeden a ten najväčší sčítanec teda určite bude číslo 16​. Musíme teda doplniť zvyšných 38-16=22​ pomocou troch sčítancov. Vieme si všimnúť, že musíme použiť aspoň dve deviatky, pretože 9+4+4 = 17​, čo je príliš málo. Teda máme ďalšie sčítance dve deviatky, a zvyšný sčítanec bude nakoniec 22 - 2\cdot9 = 4​, čo nám pekne vychádza. 

Jednotlivé sčítance budú teda: 16,9,9,4​. Hodnoty jednotlivých výrazov teda budú: 4,3,3,2​. Vieme si tak zostaviť rovnice:

a)6\leq e+d \leq 8​​
b)9\leq d+c \leq11​​
c)9\leq c+b \leq 11​​
d)12\leq b+a\leq 14​​
e) (zo zadania) a \gt b \gt c \gt d \gt e \gt 0​​

Poďme sa teraz pozerať na jednotlivé možnosti toho, akú hodnotu môže nadobúdať e​:

e=1​:
Potom z a) musí d​ byť aspoň 5​. Potom však z b) a e)c = 6​. Potom teda z e) je b​ aspoň 7​, čo však porušuje c), pretože by platilo, že c+b \geq 13​. Teda e​ nemôže byť 1​.

e = 2​:
Potom z a) musí byť d​ aspoň 4​. Z b) musí byť c​ aspoň 5​, a teda b​ aspoň 6​. Všimnime si, že keby bolo d  väčšie ako 4​, už by sa porušila podmienka c). Teda c​ môže byť najviac 5​ a b​ najviac 6​. Potom však a​ musí byť aspoň 7​. Môže byť však aj 8​.

e = 3​:
Potom z e) musí byť d) aspoň 4​. Z b) musí byť c​ aspoň 5​, a teda b​ aspoň 6​. Opäť si všimnime, že keby bolo d​ väčšie ako 4​, už by sa porušila podmienka c). Potom opäť a​ musí byť aspoň 7​, a zasa môže byť však aj 8​.

e \geq 4​:
Potom z e) musí byť d​ aspoň 5​, čo už ale poruší a). Teda nie je možné.

Vyšli nám teda 4​ riešenia pre a,b,c,d,e​:
​7,6,5,4,2
8,6,5,4,2
7,6,5,4,3
8,6,5,4,3​​​​

V tomto príklade sa chcelo ukázať, že trojuholník \triangle ABC je rovnostranný, práve vtedy keď \triangle A´B´C´ je rovnostranný. Čo znamená 2 veci. Najprv musíme ukázať, že ak \triangle ABC je rovnostranný, tak aj \triangle A´B´C´ je rovnostranný a potom naopak.

1. Nech \triangle ABC je rovnostranný. 

V rovnostrannom trojuholníku sa výška, ťažnica aj os uhla zhodujú. Takže body A´,B´,C´ sú postupne stredy strán BC, CA, AB. Preto úsečky A´B´, B´C´, C´A´ sú stredné priečky trojuholníka \triangle ABC.,  Špeciálne majú polovičné dĺžky oproti prislúchajúcim stranám \triangle ABC. Ten je rovnostranný, takže platí:

\lvert AB\rvert=2\cdot\lvert A´B´\rvert=\lvert BC\rvert=2\cdot\lvert B´C´\rvert=\lvert CA\rvert=2\cdot\lvert C´A´\rvert

Môžeme konštatovať, že \triangle A´B´C´  je tiež rovnostranný.

2. Opačne to bolo náročnejšie. Nech je \triangle A´B´C´  rovnostranný.

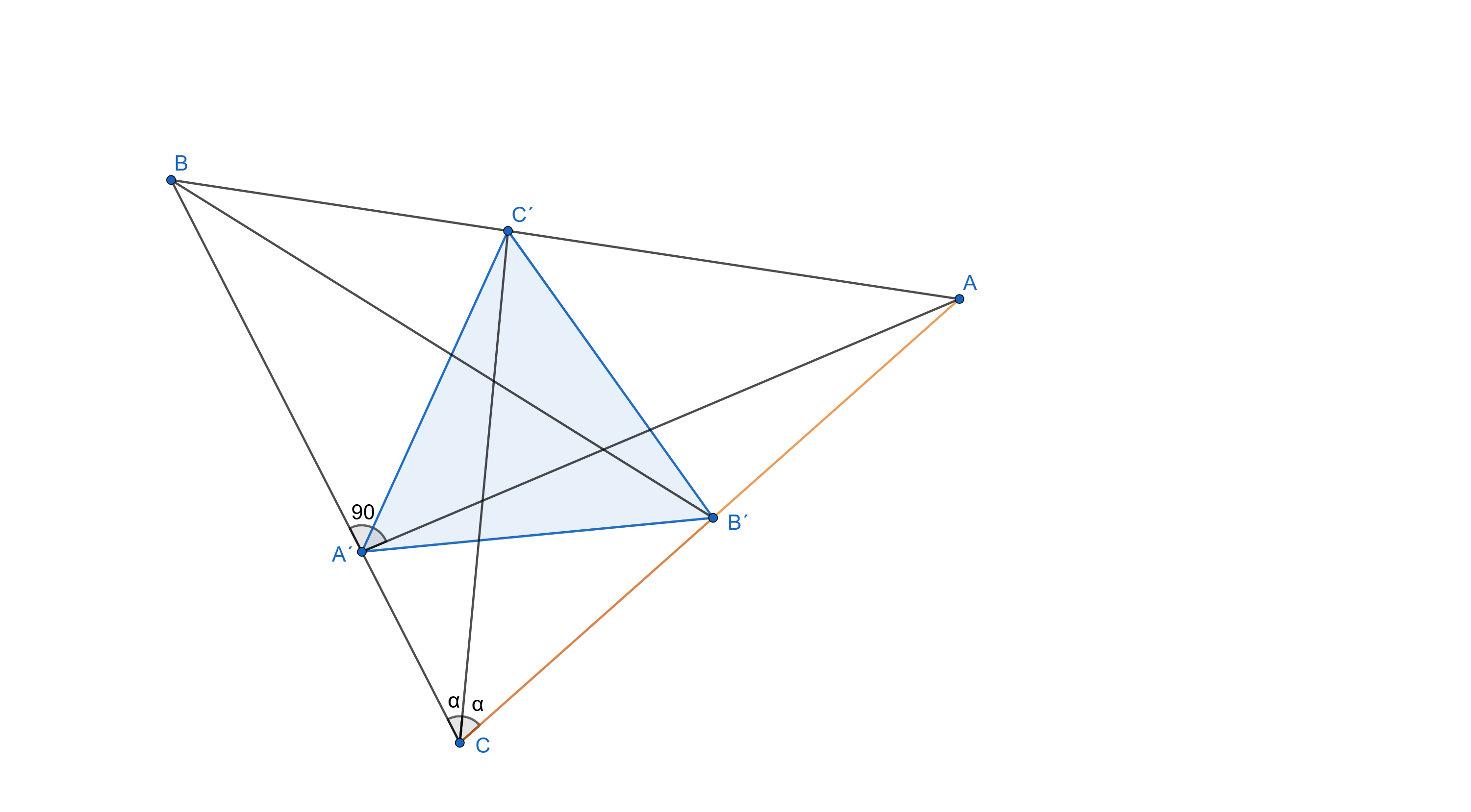
Úsečka AA´  je výška v \triangle ABC , preto je uhol \angle AA´C  pravý. Úsečka BB´  je ťažnica, takže bod B´  je stredom strany AC . Dokopy je teda bod B´  stredom Tálesovej kružnice nad trojuholníkom \triangle AA´C . Vďaka tomu platí \lvert AB´\rvert=\lvert CB´\rvert=\lvert A´B´\rvert=a . Spomeňme si na predpoklad, že trojuholník \triangle A´B´C´  je rovnostranný a dostávame \lvert A´B´\rvert=\lvert B´C´\rvert=\lvert C´A´\rvert=a .

Teraz vidíme, že body C,A,C´  ležia na kružnici so stredom v bode B´ . Takže z Tálesovej vety dostávame, že aj uhol \lvert \angle CC´A\rvert=90^\circ=\lvert \angle CC´B\rvert . Potom sú trojuholníky \triangle CC´A  a \triangle CC´B  zhodné podľa vety usu. Zdielajú stranu CC´ , pravý uhol a uhol \alpha . Znamená to, že \lvert CA\rvert=\lvert CB\rvert > a ďalej, že \lvert AC´\rvert=\lvert BC´\rvert=b .

Posledné, čo nám ostáva je všimnúť si, že aj trojuholník \triangle A´AB  je pravouhlý. Stred Tálesovej kružnice prisluchajúcej tomuto trojuholníku je bod C´ . Takže platí, že a=\lvert A´B´\rvert=\lvert AC´\rvert=\lvert BC´\rvert=b . Čím dostávame požadované tvrdenie.

Komentár

Väčšina z vás v riešení riešilo iba implikáciu, ak je trojuholník \triangle ABC  rovnostranný, tak je aj trojuholník \triangle A´B´C´  rovnostranný. Za ňu sme dávali 4 body.

Pod znakom "\_" si budeme predstavovať voľné políčko. Dokážeme, že Matej vie vyhrať bez ohľadu na to, ako hrajú vedúci.

Predstavme si, že nastane situácia:

S \_ \ \_ \ S

Ak niektorý z hráčov zahrá do niektorého z týchto dvoch voľných políčok S, tak druhý hráč môže zahrať do druhého políčka U a vyhrať. Podobne ak niektorý z hráčov zahrá do niektorého z týchto políčok U, tak druhý hráč môže zahrať do druhého políčka S a vyhrať. 

Keďže tabuľka má rozmer 2024, tak Matej vie vo svojom prvom ťahu umiestniť S tak, aby bolo aspoň 500 políčok od kraja a od políčka zaplneného vedúcimi. Potom bez ohľadu na to, čo zahrajú vedúci, Matej vie umiestniť S tak, aby vzniklo S \_ \ \_ S.  Takže od tohto momentu už hra nebude vedieť skončiť remízou. Takže nám už len stačí ukázať, že Matej vie hrať tak, aby neprehral.

Ak sa stane, že je Matej na ťahu a vie dokončiť SUS, tak ho dokončí a vyhrá. Teraz predpokladajme, že taký ťah neexistuje. Dokážeme, že Matej vie zahrať taký ťah, aby takáto situácia nevznikla. Keďže je Matej druhý hráč, keď je na ťahu, tak je nevyplnených nepárny počet políčok. To znamená, že existuje voľné políčko, ktoré má dvoch voľných, alebo dvoch zaplnených susedov. V oboch prípadoch umiestnením U do tohto voľného políčka nemôže vytvoriť situáciu, kde stačí jeden ťah na vytvorenie SUS. 

Dokázali sme, že Matej vie zaručiť, aby hra mala víťaza a navyše sme ukázali, že Matej vo svojom ťahu buď vyhrá, alebo si zaručí, že ďalší ťah nie je pre vedúcich výherný. Keďže sa hra niekedy skončí, tak Matej musí byť jej víťazom.

Odpoveď: Matej si vie zaručiť výhru bez ohľadu na to, aké ťahy hrajú vedúci.