Riešky výlet - Ahojte Rieškari, jar je v plnom prúde, vonku je pekne a my sa chystáme na výlet! Zoberte batohy, hry, frisbee, kamarátov a hlavne dobrú náladu a poďte sa s nami … Prejsť na článok
×9. príklad - Vzorové riešenie
Zadanie
Škorpión má zaujímavé klepeto trojuholníkového tvaru s vrcholmi A, B, C. Nech A’, B’, C’ sú postupne na stranách BC, AC, AB tak, že AA’ je výška, BB’ je ťažnica a CC’ je os uhla. Dokážte, že A’B’C’ je rovnostranný trojuholník práve vtedy, keď ABC je rovnostranný trojuholník.
Vzorové riešenie
V tomto príklade sa chcelo ukázať, že trojuholník \triangle ABC je rovnostranný, práve vtedy keď \triangle A´B´C´ je rovnostranný. Čo znamená 2 veci. Najprv musíme ukázať, že ak \triangle ABC je rovnostranný, tak aj \triangle A´B´C´ je rovnostranný a potom naopak.
1. Nech \triangle ABC je rovnostranný.
V rovnostrannom trojuholníku sa výška, ťažnica aj os uhla zhodujú. Takže body A´,B´,C´ sú postupne stredy strán BC, CA, AB. Preto úsečky A´B´, B´C´, C´A´ sú stredné priečky trojuholníka \triangle ABC., Špeciálne majú polovičné dĺžky oproti prislúchajúcim stranám \triangle ABC. Ten je rovnostranný, takže platí:
\lvert AB\rvert=2\cdot\lvert A´B´\rvert=\lvert BC\rvert=2\cdot\lvert B´C´\rvert=\lvert CA\rvert=2\cdot\lvert C´A´\rvert
Môžeme konštatovať, že \triangle A´B´C´ je tiež rovnostranný.
2. Opačne to bolo náročnejšie. Nech je \triangle A´B´C´ rovnostranný.
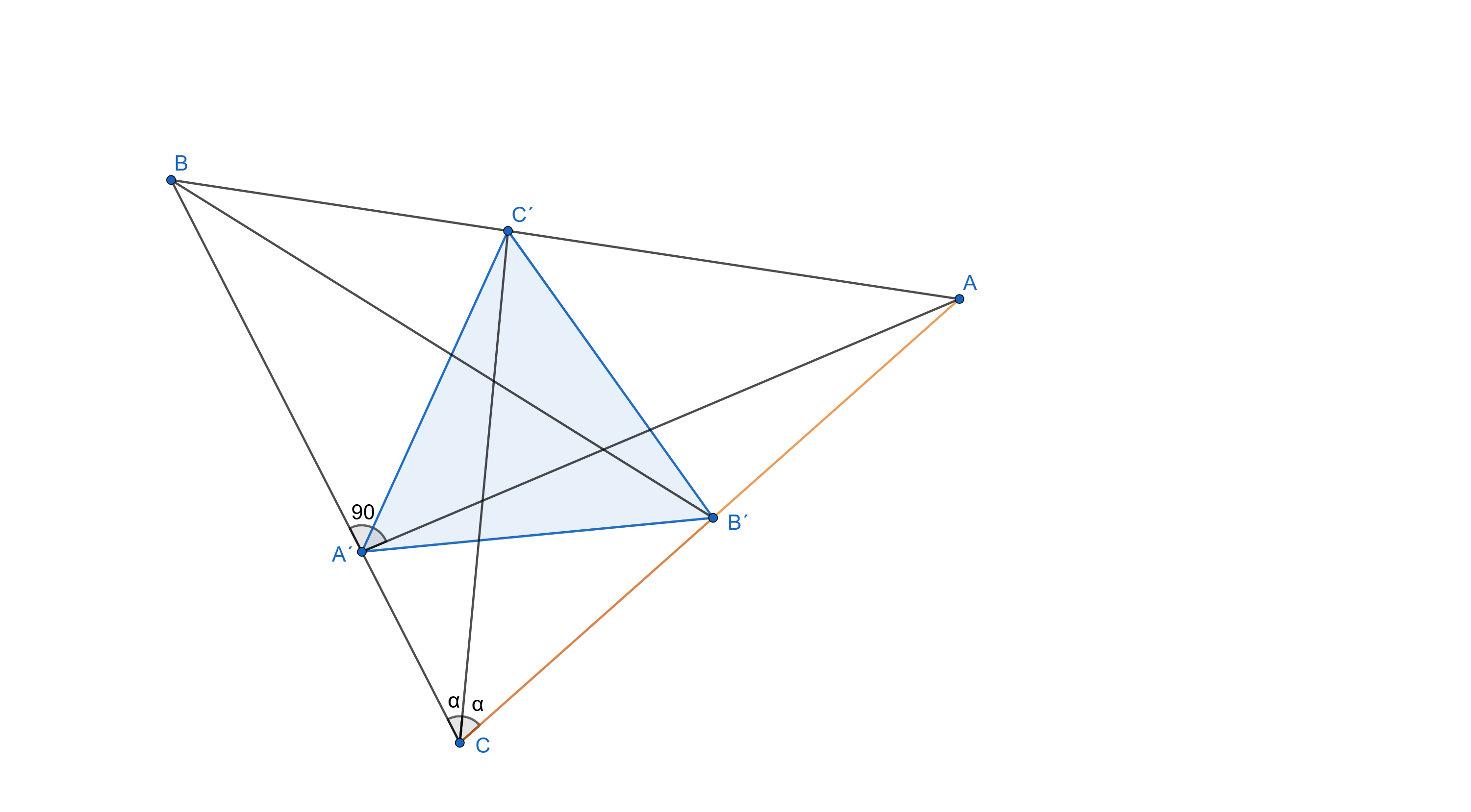
Úsečka AA´ je výška v \triangle ABC , preto je uhol \angle AA´C pravý. Úsečka BB´ je ťažnica, takže bod B´ je stredom strany AC . Dokopy je teda bod B´ stredom Tálesovej kružnice nad trojuholníkom \triangle AA´C . Vďaka tomu platí \lvert AB´\rvert=\lvert CB´\rvert=\lvert A´B´\rvert=a . Spomeňme si na predpoklad, že trojuholník \triangle A´B´C´ je rovnostranný a dostávame \lvert A´B´\rvert=\lvert B´C´\rvert=\lvert C´A´\rvert=a .
Teraz vidíme, že body C,A,C´ ležia na kružnici so stredom v bode B´ . Takže z Tálesovej vety dostávame, že aj uhol \lvert \angle CC´A\rvert=90^\circ=\lvert \angle CC´B\rvert . Potom sú trojuholníky \triangle CC´A a \triangle CC´B zhodné podľa vety usu. Zdielajú stranu CC´ , pravý uhol a uhol \alpha . Znamená to, že \lvert CA\rvert=\lvert CB\rvert > a ďalej, že \lvert AC´\rvert=\lvert BC´\rvert=b .
Posledné, čo nám ostáva je všimnúť si, že aj trojuholník \triangle A´AB je pravouhlý. Stred Tálesovej kružnice prisluchajúcej tomuto trojuholníku je bod C´ . Takže platí, že a=\lvert A´B´\rvert=\lvert AC´\rvert=\lvert BC´\rvert=b . Čím dostávame požadované tvrdenie.
Komentár
Väčšina z vás v riešení riešilo iba implikáciu, ak je trojuholník \triangle ABC rovnostranný, tak je aj trojuholník \triangle A´B´C´ rovnostranný. Za ňu sme dávali 4 body.