Riešky výlet - Ahojte Rieškari, jar je v plnom prúde, vonku je pekne a my sa chystáme na výlet! Zoberte batohy, hry, frisbee, kamarátov a hlavne dobrú náladu a poďte sa s nami … Prejsť na článok
×7. príklad - Vzorové riešenie
Zadanie
Merlin a Anička majú čierno-bielu šachovnicu 2n \times 2n. Vedúci v každom ťahu vymenia v štvorci 2\times2 všetky biele políčka za čierne políčka a všetky čierne políčka za biele políčka. Pre ktoré n sa dá po konečnom počte ťahov zjednofarebniť šachovnicu ?
Vzorové riešenie
Pre n = 1 máme 2 \times 2 šachovnicu. Každým ťahom vedúci iba vymenia medzi týmito dvoma stavmi:
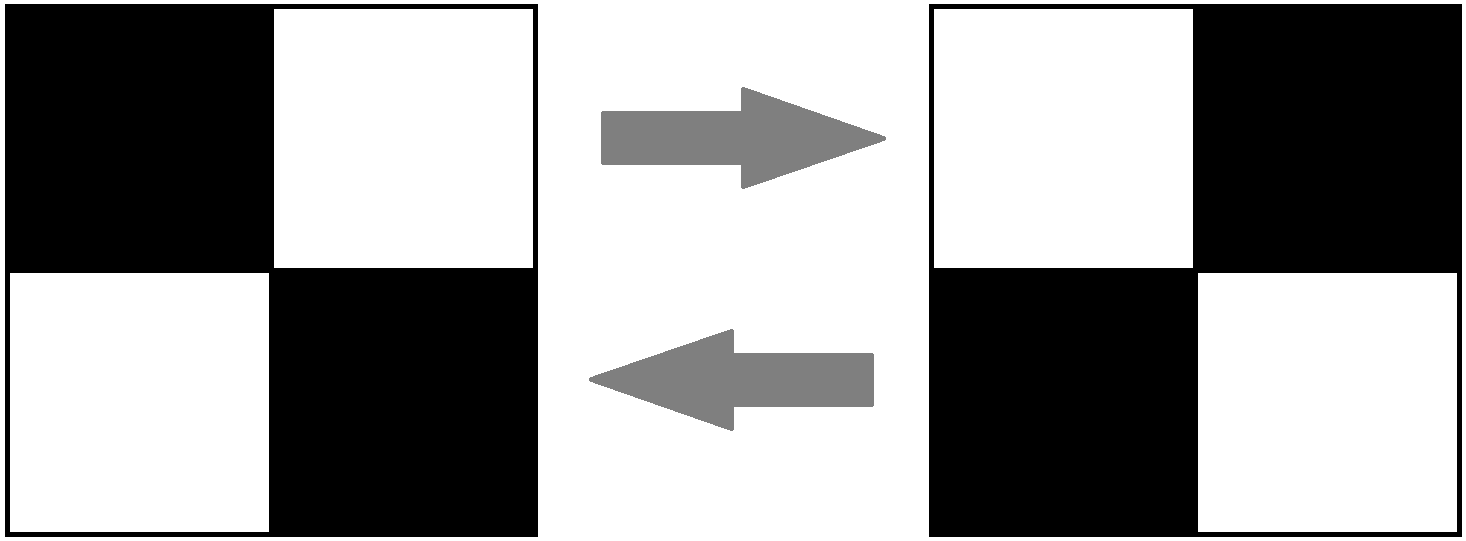
Preto sa pre n = 1 šachovnica zjednofarebniť nedá.
Keď n = 2, máme 4 \times 4 šachovnicu. Môžeme skúšať rôzne ťahy. Nie je veľmi ťažké po chvíli skúšania šachovnicu zjednofarebniť, napríklad takto:
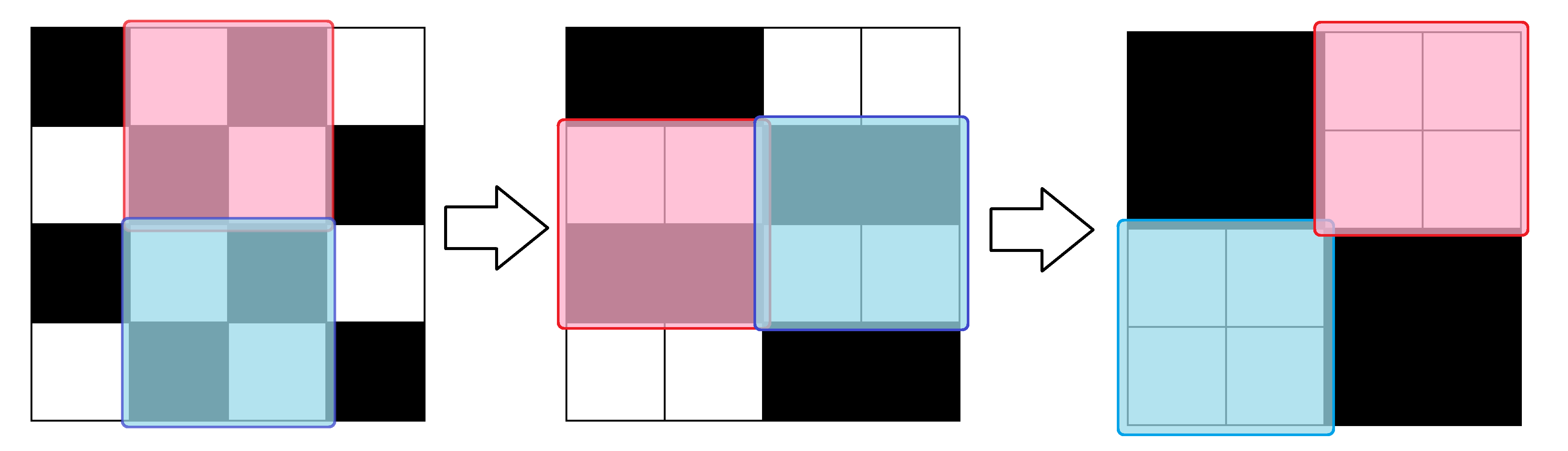
Pre n deliteľné 2 vieme šachovnicu rozdeliť na menšie 4 \times 4 štvorce. Keď je totiž n deliteľné dvomi, tak 2n je deliteľné štyrmi. Každý z týchto štvorcov môžeme potom zjednofarebniť samostatne, čím zjednofarebníme celú šachovnicu. Pre párne n sa teda šachovnica dá zjednofarebniť.
Môžeme sa snažiť zjednofarebniť šachovnicu aj pre nepárne n, ale nech robíme čo robíme, nebude sa nám to dariť. Nech sa budeme snažiť ako chceme, nepodarí sa nám zjednofarebniť ani prvý riadok tabuľky. Poďme teda skúsiť dokázať, že sa to naozaj nedá.
Pri každej výmene 2 \times 2 štvorca sa v prvom riadku môžu stať štyri veci:
- Vyberieme taký štvorec, ktorý nemá v sebe nič z prvého riadku, teda nijako prvý riadok neovplyvní
- Vyberieme štvorec, ktorý má v prvom riadku jedno čierne a jedno biele políčko. Biele políčko teda zmeníme na čierne a čierne na biele, dokopy teda nezmeníme počet bielych a čiernych políčok v prvom riadku
- Vyberieme štvorec, ktorý má v prvom riadku dve biele políčka. Obe zmeníme na čierne a teda prvý riadok má o dve biele políčka menej a o dve čierne viac.
- Vyberieme štvorec, ktorý má v prvom riadku dve čierne políčka. Obe zmeníme na biele a tak sú v prvom riadku teraz o dve čierne políčka menej a o dve biele viac.
Vidíme teda, že vždy vieme premieňať čierne políčka na biele a naopak len po dvoch - buď ich počty nezmeníme, alebo ich zvýšime / znížime rovno o 2.
Na začiatku máme v prvom riadku n bielych a n čiernych políčok. Keď je n nepárne, tak ich je nepárny počet. My ale tento počet vieme meniť vždy len o 2. Keď pripočítavame alebo odpočítavame od nepárneho čísla 2, dostaneme vždy len nepárne číslo, teda vždy budeme mať nepárny počet čiernych a nepárny počet bielych políčok v prvom riadku.
Na konci by sme chceli mať 0 políčok jednej farby a 2n tej druhej. To sú ale obe párne čísla, takže ich iba pripočítavaním a odpočítavaním 2 nevieme dosiahnuť.
Odpoveď:
Pre párne n sa šachovnica zjednofarebniť dá, pre nepárne sa nedá.