Vzorové riešenia 3. kola

Všimnime si, že všetky čísla, ktoré mohli ľudia mať na chrbte, sú kladné. To znamená, že akonáhle máme súčet väčší než 52 a ešte niektorí nemajú číslo na chrbte, tak máme nevyhovujúcu možnosť. Z tohto vyplýva, že naši trinásti ľudia nemôžu mať medzi sebou 11 pätiek alebo viac, lebo by náš súčet čísel bol príliš veľký.

Navyše, s trochu hlbšou úvahou vieme zistiť, že ani desať pätiek nie je možných. Ak by sme ich mali desať, tak to samo o sebe dáva súčet 50 a ešte traja ľudia potrebujú dostať číslo. Všimnime si, že títo traja dostanú najmenej súčet 3, ak im dáme jednotky (a ak im dáme väčsie čísla, tak sa im súčet samozrejme zvýši). To ale dokopy dáva súčet prinajmenšom 53 \gt 52, čo nevyhovuje.

Preto pätiek je najviac deväť. Všimnime si, že deväť by ich byť mohlo, keď zvyšným ľuďom rozdáme tri dvojky a jednu jednotku, lebo 9 \cdot 5 + 3 \cdot 2 + 1 \cdot 1 = 52.

To je aj jediná možnosť, ktorá vyhovuje zadaniu a to teraz dokážeme. Presnejšie, ukážeme, že súčet čísel už bude primalý, nech už čísla prideľujeme akokoľvek. Keďže súčty budú malé, rovno môžeme priraďovať iba dvojky a päťky, lebo jednotky by situáciu iba zhoršili. Ak máme 8 pätiek, tak náš súčet je najviac 8 \cdot 5 + 5 \cdot 2 = 50 \lt 52 . Za každú ďalšiu päťku, ktorú odoberieme, sa náš maximálny možný súčet zmenší o tri. Preto menšie počty ani nemusíme skúšať.

Odpoveď: Jediná možnosť je, že deväť ľudí má na chrbte 5, traja majú 2 a ten posledný trinásty má 1.

Komentár

Príklad sa vám zväčša podaril. No ak skúšate možnosti, treba ich vyskúšať naozaj všetky. Druhá možnosť, ktorú máte, je popísať, prečo iné možnosti nemá zmysel skúšať, tak ako sme to práve urobili vo vzorovom riešení.

Môžeme si všimnúť, že ak si pri Zuzke zvolíme jej jediný pravdivý výrok ľubovoľne, tak tento jej výrok jednoznačne určí, ktorý Peťkov výrok musí byť pravdivý. To nám dá 4, ktoré treba otestovať, či môžu nastať:​

1. Zuzkin pravdivý výrok je Oliver bol ​1​. Peťkov pravdivý výrok musí byť Danko bol 4. Je to preto, lebo jeho prvý výrok nemôže byť pravda, inak by na 1. mieste boli dvaja rôzny ľudia, jeho druhý výrok nemôže byť pravdivý, lebo zo Zuzkiných výrokov plynie, že Johnny nemôže byť 2. a jeho tretí výrok nemôže byť pravdivý preto, lebo v ňom hovorí o pozícii Olivera, ktorý je už na prvom mieste. Tým pádom iba jeho štvrtý výrok môže byť pravdivý.
2. Zuzkin pravdivý výrok je Johnny bol 2​. Peťkov pravdivý výrok teda musí byť tiež Johnny bol 2.
3. Zuzkin pravdivý výrok je Danko bol ​3. Peťkov pravdivý výrok musí byť Erik bol 1. Je to z rovnkého dôvody ako pri prvej možnosti.
4. Zuzkin pravdivý výrok je Erik bol 4. Peťkov pravdivý výrok musí byť Oliver bol 3. Je to z rovnakého dôvodu ako pri prvej možnosti.

​1. možnosť: Môžeme si všimnúť, že buď Johnny alebo Erik musia byť na druhom mieste. Katka vždy klame a z jej výrokov plynie, že Erik nemôže byť 2. Peťko a Zuzka už raz hovoria pravdu, takže ich ostatné výroky nie sú pravdivé. Čiže ani Johnny nemôže byť 2. Z toho plynie, že nikto z nich nemôže byť druhý, takže táto možnosť nie je správna.

2​. možnosť: Podľa Katky nemôže byť Danko 1., podľa Zuzky nemôže byť 3., podľa Peťka nemôže byť 4. Ostáva mu iba 2. miesto, ale tam už je Johnny, takže ani táto možnosť nie je správna.

3. možnosť: Na 2. mieste musí byť Oliver, lebo Danko aj Erik už majú priradené miesto a Johnny nemôže byť 2. Tým pádom Johnnymu ostáva 4. miesto. Výsledné poradie je Erik 1., Oliver 2​., Danko 3. a Johnny 4. Teraz stačí spraviť skúšku správnosti a porovnať túto možnosť s výrokmi v zadaní. Všetky Katkine tvrdenie sú nesprávne, jedno Zuzkine tvrdenie je správne, ostané sú nesprávne, jedno Peťkovo tvrdenie je správne, ostatné sú nesprávne. To sa zhoduje so zadaním, takže toto je správna možnosť.

4. možnosť: Na 1. mieste musí byť Johnny, lebo Oliver aj Erik majú už určené pozície a Danko nemôže byť 1. Tým pádom Dankovi ostáva už iba 2​. miesto. Výsledné poradie je Johnny 1., Danko 2., Oliver 3. a Erik 4. Teraz stačí spraviť skúšku správnosti a porovnať túto možnosť s výrokmi v zadaní. Všetky Katkine tvrdenie sú nesprávne, jedno Zuzkine tvrdenie je správne, ostané sú nesprávne, jedno Peťkovo tvrdenie je správne, ostatné sú nesprávne. To sa zhoduje so zadaním, takže toto je správna možnosť.

Odpoveď: Sú dve poradia, ako mohli útočiť:

• ​Erik 1​., Oliver 2​​., Danko 3​. a Johnny 4​.
  
• Johnny 1​., Danko 2​., Oliver 3​. a Erik 4​.
  

Komentár

Väčšina z vás zvládla príklad na plný počet bodov. Bolo treba si dať pozor na to, ktoré možnosti treba a ktoré netreba skúšať. Takisto nie je na škodu po nájdení možnosti urobiť skúšku správnosti a overiť si, či daná možnosť naozaj spĺňa podmienky zo zadania.

Ako prvé sa pozrime na úlohu a.

Môžme si všimnúť že ak si vezmeme 4​ kocky, tak ich vieme usporiadať do štvorca 2 \times 2​ takým spôsobom, že navrchu bude mať každá kocka číslo a. Takéto usporiadanie bude vyzerať nasledovne:

Vidíme, že všetky kocky v tomto rozložení sú rovnaké len otočené.

Pri takomto rozložení môžme spraviť z ďaľších štyroch kociek taký istý štvorec a tieto dva štvorce dať stranami s číslami a k sebe a dostaneme kocku, ktorá spĺňa zadanie. To preto, že na prvom "poschodí" vidíme, že sú všetky susediace čísla rovnaké, to znamená že aj na druhom "poschodí" budú susediace čísla rovnaké. Navyše kedže spájame dve štvorice, ktoré majú iba a, tak aj susediace čísla medzi "poschodiami" budú rovnaké.

Pozrime sa teraz na úlohu b.

V tejto úlohe si môžeme všimnúť, že ak dokážeme, že po spojení dvoch kociek nebudeme vedieť dostať na 4​ susediacich stranách (2​ strany veľkosti 2 \times 1 susediace hranou a 2 strany veľkosti 1 \times 1 oproti sebe) dokopy najviac 3​ rôzne čísla, potom nedokážeme vytvoriť kocku tak, aby mala na povrchu iba 3 rôzne čísla. Celá naša kocka sa totiž skladá zo 4 takýchto dvojíc a každá prispieva povrchu práve 4 stenami.​

Zoberme dve kocky a priložme ich rovnakým číslom k sebe, nech je toto číslo napríklad 6​. Potom na druhej strane každej kocky bude číslo 1. Takže na obvode už mám jedno číslo a strany 2 \times 1 môžu mať dokopy najviac 2 rôzne čísla.​

Teraz si môžme všimnúť že ak máme na kocke vľavo čísla na stranách napríklad v poradí 3, 5, 4, 2 tak na kocke vpravo budeme mať čísla v poradí 2, 4, 5, 3. To preto, že ak sú kocky otočené k sebe rovnakým číslom tak jedna je otočená o 180 stupňov (v rovnakom poradí by bola ak by bola zrkadlovo otočená a to by už bola iná kocka), takže aj jej ostatné strany sa otočia. Ak sa teda pozrieme na tie dve strany ktoré susedia spolu tak budú vyzerať nasledovne:

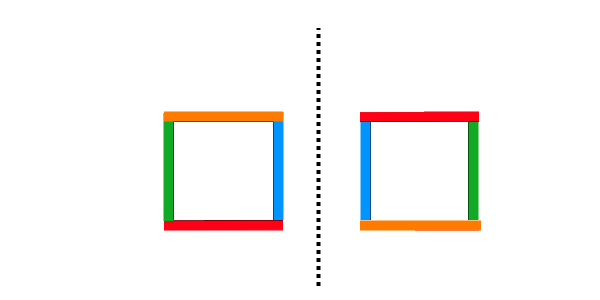
(V obrázku sa pozeráme pri oboch kockách na číslo, ktorým sa dotýkajú takže nám na okrajoch susedia modrá s modrou a zelená so zelenou.)

​​Z tohto je jasne vidno, že nech jednu z nich otáčame akokoľvek, tak vždy bude platiť že na stranách 2 \times 1 budú buď rôzne čísla, alebo každá druhá strana bude mať rovnaké čísla a každá druhá rôzne.  Dokopy sú to vždy aspoň 3 čísla, čo je viac ako môže byť na splnenie zadania.

To znamená že neviem vybrať 2 priľahlé strany tak aby mali na sebe maximálne 2 rôzne čísla. Neviem teda ani vytvoriť kocku 2 \times 2 \times 2 tak, aby spĺňala podmienky úlohy.

Odpoveď:

a) Dokážeme vytvoriť.

b) Nedokážeme vytvoriť.

Ako prvé sme si mohli všimnúť, že každé zo zaokrúhlených čísel bude mať na mieste jednotiek 0​. To znamená, že cifra 3​ v súčte 5443​ je daná pôvodným číslom n​, ktoré zaokrúhlené nie je, a teda n​ sa končí trojkou.

Pre prehľadnosť si zapíšeme zadanie vo forme písmen:

\begin{array}{ccccc} & A & B & C & 3 \\ +& A & B & C & 0\\ +& A' & B' & 0 & 0\\ +& A' & 0 & 0 & 0\\ \hline & 5 & 4 & 4 & 3\end{array}

Kde čiarka znamená, že táto cifra bude buď zhodná s cifrou v pôvodnom čísle, alebo o jedna väčšia. V prípade, že by sme mali v dôsledku zaokrúhľovania zväčšiť o jedna cifru 9​, napíšeme namiesto nej 0​ a o jedna zväčšíme nasledujúcu cifru. Preto má v čísle n​ zaokrúhlenom na stovky v indexe čiarku aj cifra A'​. Cifra C​ čiarku nemá vôbec, keďže trojka zaokrúhľuje nadol.

Vidíme, že súčet dvoch cifier  C​ sa musí končiť cifrou 4​. Súčet dvoch jednociferných čísel môže byť najviac 18​, teda prichádzajú do úvahy dve rôzne hodnoty C​, a to C = 2, kedy bude súčet 4​ a C = 7, kedy bude súčet 14​.

Pozrime sa na prípad C = 2​. Dvojka zaokrúhľuje nadol, a teda súčet troch zhodných B musí v súčte na mieste stoviek vytvoriť cifru 4​. Súčet troch jednociferných čísel je najviac 27, a teda prichádzajú do úvahy súčty 4​, 14​ a 24​, z čoho je deliteľné tromi len číslo 24​. To znamená, že B = 8​. Pre číslo A​ platí, že musí byť väčšie ako 0​, v opačnom prípade by n nebolo štvorciferné. Ak by sme uvažovali na mieste A​ cifru 2​ a viac, súčet by bol najmenej 8000​. To znamená, že na mieste tisícok bude určite 1​. (Tento poznatok si zapamätajme, zíde sa nám aj pri C = 7​.) Skúsme teda dosadiť:

\begin{array}{ccccc} & 1 & 8 & 2 & 3 \\ +& 1 & 8 & 2 & 0\\ +& 1 & 8 & 0 & 0\\ +& 2 & 0 & 0 & 0\\ \hline & 7 & 4 & 4 & 3\end{array}

Vidíme, že súčet je väčší, to znamená, že C​ nemôže byť 2​.

Poďme sa teda pozrieť na prípad C = 7​. Sedmička zaokrúhľuje nahor a okrem toho nám jedna zostane zo súčtu 14​. To znamená, že 3 \cdot B + 2​ sa musí končiť štvorkou, a keďže toto môže byť najviac 29​, opäť prichádzajú do úvahy tri možné súčty: 3 \cdot B = 2​ alebo 12​ alebo 22​. Tromi je deliteľných len 12​, čiže B = 4​. Skúsme dosadiť:

\begin{array}{ccccc} & 1 & 4 & 7 & 3 \\ +& 1 & 4 & 7 & 0\\ +& 1 & 5 & 0 & 0\\ +& 1 & 0 & 0 & 0\\ \hline & 5 & 4 & 4 & 3\end{array}

A vidíme, že číslo 1473​ skutočne je hľadaným n​.

Iné riešenie

Mnohí ste sa na úlohu pozreli z iného hľadiska a k riešeniu ste sa dostali pomocou priemerov a odhadov. Zistili ste napríklad, že hľadané číslo n​ musí byť menšie ako 1500​, keďže v opačnom prípade by sa číslo na tisícky zaokrúhľovalo nahor, a výsledok by bol aspoň 6500​:

\begin{array}{ccccc} & 1 & 5 & 0 & 0 \\ +& 1 & 5 & 0 & 0\\ +& 1 & 5 & 0 & 0\\ +& 2 & 0 & 0 & 0\\ \hline & 6 & 5 & 0 & 0\end{array}

Takto vieme, že posledné zaokrúhlené číslo musí byť 1000​, a teda súčet zvyšných troch je 4443​. Priemerná hodnota je 4443 : 3 = 1481​ takže máme približnú hodnotu, blízko ktorej by malo byť aj naše číslo n. V tomto bode bola správna otázka, či číslo n​ vie byť menšie ako 1450​ a odpoveď je, že nie, pretože na to, aby sme dosiahli priemer 1481​ sa musí číslo na stovky zaokrúhliť na 1500​. Vieme teda, že A = 1​, B = 4​, C\ge 5​ a na mieste jednotiek bude trojka. C​ vieme už ľahko dopočítať a dostať sa tak k správnemu výsledku n = 1473​

Komentár

Celkovo úloha dopadla veľmi dobre, každý sa dopracoval aspoň k časti informácií o čísle n​ a väčšina aj k správnemu výsledku 1473​. Potešilo ma to :))

Mnohí ste ale pri C = 2​ zabudli, že B​ môže byť aj 8​, keďže súčet troch cifier môže byť až 27​. Keďže takýto prípad mohol potenciálne viesť k správnemu riešeniu, bolo potrebné ho dôsledne preveriť.

V tejto úlohe vlastne hľadáme nejaké veľké číslo, ktoré je násobkom všetkých čísel do 14 okrem dvoch. A vlastne ho ani nemusíme nájsť, ak budeme bez toho vedieť isto pofvedať, ktoré čísla ho budú deliť. O niektorých číslach vieme rýchlo povedať či môžu byť ich výroky nepravdivé. Číslo bude určite násobkom jednotky, ako každé prirodzené číslo, teda prvý výrok bude pravdivý. Vieme dokázať aj to, že číslo bude násobkom dvojky, teda bude párne. Ak by nebolo, nemohlo by byť ani násobkom žiadneho iného párneho čísla, tie sú všetky vždy párne. A to by potom bolo nepravdivých veľa informácií.

Vlastne si môžeme uvedomiť že takéto pravidlo platí pre všetky čísla. Ak nejaké číslo nie je deliteľné číslom n, tak nemôže byť deliteľné ani žiadnym násobkom n. Lebo ak je napríklad naše číslo deliteľné 14 (7 \cdot 2), tak je deliteľné bezo zvyšku aj 7, a dostaneme 2-krát väčší výsledok. Toto je pre všetky čísla po 7 problém, lebo ak by bol výrok o nich nepravdivý, musel by byť aj o čísle dva krát väčšom, no podľa zadania sú iba po sebe idúce výroky nepravdivé (okrem pre čísla 1 a 2, tie sú po sebe idúce ale o nich vieme, že číslo delia).

Teda vieme, že naše číslo je deliteľné všetkými číslami od 1 po 7. Môžeme sa skúsiť pozrieť, či nám tieto čísla nestačia na to, aby sme vedeli niečo povedať o ostatných. Pozrime sa preto na číslo 10. Jednoduché pravidlo delenia 10-timi hovorí, že ak je číslo deliteľné 5 a zároveň 2, je deliteľné aj 10. Podobne poznáme podmienku pre deliteľnosť 12 - deliteľnosť 3 a zároveň 4, a 14 - deliteľnosť 7 a zároveň 2. Všetky tieto čísla už vieme že naše číslo delia, takže môžeme to isté povedať aj o 10, 12 a 14.

Ak tieto pravidlá nepoznáme, môžeme si odvodiť pravidlo aj sami. Vždy zisťujeme deliteľnosť dvomi číslami, ktorých súčin nám dá číslo, na ktoré sa pýtame. Tu si však treba dať pozor, že toto NESTAČÍ. Napríklad pre deliteľnosť 12-kou nestačí, aby bolo číslo deliteľné 6 a 2. 2-ka je už totiž v čísle 6 “schovaná” a neprináša nám žiadnu novú informáciu, pretože všetko deliteľné šiestimi je deliteľné aj dvomi. Nutná podmienka teda je, aby tieto čísla nemali žiadneho spoločného deliteľa okrem 1. Preto pri deliteľnosti 12-timi používame čísla 3 a 4.

Keď už máme informácie o všetkých týchto číslach, že sú ich výroky pravdivé. Môžeme sa pozrieť, ktoré čísla by teda mohli mať výroky nepravdivé a teda veľké číslo nedeliť. Sú to dve po sebe idúce čísla, takže to už nemôžu byť 13 ani 11. Jediné zostávajúce čísla sú teda 8 a 9. Ich výroky teda musia byť nepravdivé, lebo sme ukázali že podľa podmienok žiadne iné byť nepravdivé nemôžu.

Ak by sme si chceli overiť, či také niečo môže nastať, nájdeme číslo 60~060 (najmenší spoločný násobok všetkých pravdivých čísel), pri ktorom sú naozaj nepravdivé len výroky 8 a 9.

Odpoveď: Nepravdivé sú výroky 8​ a 9​.

Označíme AD \cap BE = K, BE \cap CF = L, CF \cap DG = M a CF \cap DA = N. Ďalej uhol v cípe pri vrchole A označíme \sphericalangle A, uhol v cípe pri vrchole B označíme \sphericalangle B, atď.

Pozrime sa na trojuholník AEK, keďže súčet vnútorných uhlov v trojuholníku je 180 \degree, tak platí rovnosť 180 \degree = |\sphericalangle A| + |\sphericalangle E| + |\sphericalangle AKE|, teda |\sphericalangle AKE| = 180 \degree - |\sphericalangle A| - |\sphericalangle E|. Keďže A, K, D ležia na priamke, tak |\sphericalangle AKD| = 180 \degree, ale taktiež |\sphericalangle AKD| = |\sphericalangle AKE| + |\sphericalangle EKD|, čiže dostávame 180 \degree = |\sphericalangle AKE| + |\sphericalangle EKD|, po dosadení |\sphericalangle AKE| = 180 \degree -|\sphericalangle A| - |\sphericalangle E| a upravení dostávame |\sphericalangle EKD| = |\sphericalangle A| + |\sphericalangle E|.

Analogicky z trojuholníka BFL dostávame |\sphericalangle BLC| = |\sphericalangle B| + |\sphericalangle F| a z trojuholníka CGM dostávame |\sphericalangle CMD| = |\sphericalangle C| + |\sphericalangle G|.

Teraz však poznáme 2 vnútorné uhly trojuholníka MND, takže postupom ako doteraz dostaneme |\sphericalangle LNK| = |\sphericalangle CMD| + |\sphericalangle NDM| = |\sphericalangle G| + |\sphericalangle C| + |\sphericalangle D|.

|\sphericalangle BLC| = |\sphericalangle KLN|, lebo K \in LB a N \in CL. Rovnako |\sphericalangle EKD| = |\sphericalangle LKN|, lebo L \in KE a N \in DK. Teraz keď sa pozrieme na vnútorné uhly trojuholníka KLN, tak dostaneme 180 \degree = |\sphericalangle LKN| + |\sphericalangle KNL| + |\sphericalangle NLK| = |\sphericalangle A| + |\sphericalangle E| + |\sphericalangle G| + |\sphericalangle C| + |\sphericalangle D| + |\sphericalangle B| + |\sphericalangle F|, čo je súčet všetkých uhlov v cípoch sedemcípej hviezdy.

Čo ak body K, L, N ležia na priamke a teda netvoria trojuholník? Keďže L \in BE \cap CF a N \in DA \cap CF, tak aj K \in CF, lebo body L a N už definujú priamku. Ale K \in AD \cap BE, takže priamky AD, BE, CF sa pretnú v jednom bode a teda body K, L, M sú jeden bod. Potom |\sphericalangle EKD| = |\sphericalangle AKB|, lebo sú vrcholové, |\sphericalangle BLC| = |\sphericalangle BKC|, lebo L = K, z trojuholníka MDK platí, že |\sphericalangle MKA| = |\sphericalangle D| + |\sphericalangle CMD| a |\sphericalangle MKA| = |\sphericalangle FKA|, lebo K, M, F ležia na priamke. Uhly |\sphericalangle FKA|, |\sphericalangle AKB| a |\sphericalangle BKC| v súčte majú 180 \degree , lebo tvoria priamku CF, ale zároveň majú súčet všetkých vnútorných uhlov sedemcípej hviezdy, ich veľkosti poznáme z predošlých odsekov.

Trikové riešenie

Pozrime sa na úsečku AD, jej otočením o |\sphericalangle D| v smere hodinových ručičiek sa nám zobrazí do GD. Otočením GD o |\sphericalangle G| v smere hodinových ručičiek sa nám zobrazí do GC. Otočením GC o |\sphericalangle C| v smere hodinových ručičiek sa nám zobrazí do FC. Otočením FC o |\sphericalangle F| v smere hodinových ručičiek sa nám zobrazí do FB. Otočením FB o |\sphericalangle B| v smere hodinových ručičiek sa nám zobrazí do EB. Otočením EB o |\sphericalangle E| v smere hodinových ručičiek sa nám zobrazí do EA. Otočením EA o |\sphericalangle A| v smere hodinových ručičiek sa nám zobrazí do DA.

Celkovo sme úsečku AD otočili o súčet vnútorných uhlov v cípoch. Otáčali sme úsečku stále tým istým smerom a úsečka AD sa zobrazila do DA, to znamená, že sme ju celkovo otočili o 180 \degree + n \times 360 \degree. Pri zobrazovaní bodu A(G, F, E), sme nikdy neprekročili bod D, teda sme nemohli presiahnuť 360 \degree a teda súčet vnútorných uhlov musí byť 180 \degree.

Odpoveď: Súčet vnútorných uhlov sedemcípej hviezdy je 180\degree.

Ako prvé si môžeme všimnúť, že hráč vyhrá, ak má na svojom ťahu 1 papierik. Toto platí preto, že ak hráč dostal na svojom ťahu 1 papierik, tak jeho súper nemohol použiť predošlý ťah rozdelenie papierika, a teda ak on rozdelí tento jeden papierik, súper musí odobrať 2 papieriky a náš hráč vyhrá.

Ďalej si môžeme všimnúť, že vždy po 2​ ťahoch sa počet papierikov zníži, lebo viem raz "pridať" papierik jeho rozdelením a druhý hráč musí odobrať 2 alebo 3 papieriky (toto môžeme spraviť aj v opačnom poradí, t. j. uberieme a potom rozdelíme).

Poslednú vec ktorú si musíme uvedomiť je, že vždy keď rozdelí jeden hráč na svojom ťahu papierik, tak druhý hráč v nasledujúcom ťahu určite nedostane iba 1 papierik.

Teraz si teda môžeme spojiť tieto informácie a všimnúť si, že ak prvý hráč každý ťah rozdelí jeden papierik na dva tak vyhrá. To preto, že počet papierikov sa vždy znižuje medzi jeho ťahmi a zároveň jeho súper nikdy nemôže dostať iba 1 papierik. To znamená, že raz to musí byť on, kto dostane 1​ alebo žiaden papierik, čo sú pre neho výherné stavy. Teraz sa ešte musíme pozrieť na to, či nie je iný počet papierikov ako 1 víťazný pre druhého hráča:

Ak má druhý hráč na začiatku svojho ťahu viac ako 4 papieriky tak prvý hráč dostane aspoň 1 papierik a môže rozdeliť jeden papierik.
Ak má druhý hráč na začiatku 3 papieriky tak môže odobrať 2​ alebo 3​, ak odoberie 2 tak prvý hráč dostane 1​ papierik a vyhrá, a ak odoberie 3, tak prvý hráč nemá žiadne papieriky a teda vyhrá.
Ak má druhý hráč na začiatku 2​ papieriky, tak musí odobrať 2​ a prvý hráč vyhrá.
Druhý hráč nemôže dostať 1​ papierik, lebo prvý hráč každé kolo rozdelil jeden papierik na dva.

To znamená že prvý hráč má vždy výhernú stratégiu.

Odpoveď:Pre každé n vyhrá Peťko.

Predvedieme riešenie, ktoré pokryje ľubovoľný trojuholník. Nebudeme sa teda musieť venovať zvlášť rovnostranným ani iným trojuholníkom.

Zatiaľ nevieme, či bod X existuje, alebo nie. V takejto situúcií je vhodné na úvod predpokladať, že áno, a zistiť aké vlastnosti musí mať. Podľa týchto vlastností potom môžeme zúžiť počet možných kandidátov a buď vybrať takých, ktorí zadanie spĺňajú, alebo ukázať, že žiadny takí nie sú.

Čo nám teda zadanie hovorí o bode X? Má ležať vnútri nášho trojuholníka a každá priamka, ktorá ním prechádza, má deliť tento trojuholník na dve časti s rovnakým obsahom. Zvoľme si teda konkrétnu priamku — priamku z vrchola trojuholníka.

Keďže X leží vnútri, táto priamka rozdelí protiľahlú základňu na dve časti. Ich dĺžky označíme a,\, b. To budú zároveň základne trojuholníkov, ktoré vznikli týmto rozdelením. Výšku v majú tieto trojuholníky spoločnú, je to výška pôvodného trojuholníka. Na to, aby mali rovnaký obsah, musí platiť

\dfrac{av}{2} = \dfrac{bv}{2}.

To však znamená, že a = b. Naša priamka teda prechádza nie len vrcholom, ale aj stredom protiľahlej strany. Náš bod X teda musí ležať na ťažnici. Tento postup navyše vieme zopakovať aj pre zvyšné dva vrcholy, takže bod X musí ležať na všetkých troch ťažniciach. Taký bod je však iba jeden a tým je ťažisko trojuholníka.

Máme jediného kandidáta na bod X a tri priamky, ktoré cezeň prechádzajú a skutočne delia trojuholník na polovicu. Teraz musíme buď ukázať, že to spĺňajú aj ostatné priamky prechádzajúce X, alebo nájsť protipríklad. Podľa toho buď bude alebo nebude takýto bod existovať.

Po chvíli hrania sa s priamkami prechádzajúcimi ťažiskom zistíme, že správna cesta je tá druhá. Jednou takouto nevyhovujúcou priamkou je rovnobežka s niektorou stranou trojuholníka.

Označme si vrcholy ako na obrázku. Priamka p je rovnobežná s AB, prechádza ťažiskom, a zvyšné strany pretína v bodoch D a E. Pre poriadok označíme ešte Y stred strany AB.

Pozrime sa teraz na trojuholníky DXC a AYC. Keďže p a AB sú rovnobežky, uhly \sphericalangle CDX a \sphericalangle CAY sú súhlasné a teda rovnako veľké. Uhol \sphericalangle AXY majú oba trojuholníky spoločný. Sú teda podobné podľa vety uu. Keďže však má byť X ťažisko a CY ťažnica, vieme vypočítať aj koeficient podobnosti. Ťažisko leží v dvoch tretinách ťažnice, takže |CX| = \frac{2}{3} |CY|. Rovnako bude skrátená každá dĺžka, takže aj základňa, aj výška. Platí teda

\dfrac{|DX| \cdot v_{DX}}{2} = \dfrac{\frac{2}{3}a \cdot \frac{2}{3}v}{2} = \dfrac{4}{9} \cdot \dfrac{av}{2},

pričom a a v sú základňa a výška trojuholníka AYC. Trojuholník DXC má teda obsah \frac{4}{9} obsahu AYC, čo je zas polovica obsahu celého nášho trojuholníka. Samotné DXC tvorí teda \frac{2}{9} obsahu ABC.

Môžeme si všimnúť všimnúť, že rovnaký postup prejde aj pri trojuholníkoch XEC a YBC. Tie budú opäť podobné s rovnakým koeficientom podobnosti a ich obsahy budú v opäť rovnakom pomere. Aj YBC tvorí polovicu nášho trojuholníka, takže aj XEC bude tvoriť \frac{2}{9} obsahu.

Vráťme sa teda k priamke p. Tá delí náš trojuholník na dve časti. Jednou z nich je trojuholník DEC, o ktorom vieme, že tvorí \frac{2}{9} + \frac{2}{9} = \frac{4}{9} obsahu trojuholníka ABC. Aby však bod X spĺňal zadanie, musela by to byť polovica. Vidíme teda, že ani ťažisko zadaniu nevyhovuje.

Odpoveď: Bod X spĺňajúci podmienky zo zadania neexistuje v žiadnom trojuholníku.

Komentár

Väčšina z vás zvolila obdobu riešenia, ktoré vidíte vyššie, poniektorí sa však pustili aj do o niečo komplikovanejších postupov. Spôsobov ako previesť jednotlivé kroky bolo hneď niekoľko.

V prípade ťažiska sa dalo napríklad povedať, že ak bodom X neprechádza ťažnica, prechádza ním nejaká rovnobežka s ňou. Keďže však ťažnica tento trojuholník delí na polovicu, takáto rovnobežka ho deliť nemôže. V prípade priamky p sa dalo napríklad porovnať obsahy trojuholníka DEC a lichobežníka ABDE, ktoré nemohli vyjsť rovnaké.

Aj keď ste základ mali často podobný, nevyhli ste sa ani chybám. Najčastejšie ste práve umiestnili bod X na ťažnicu preto, lebo ťažnica delí trojuholník na polovicu. To však bez úvahy zo vzoráku (alebo nejakej inej) nemôžete. My totiž nevieme nič o priamkach, ktoré bodom X neprechádzajú, tie nemajú zakázané deliť trojuholník na polovicu.

Okrem toho ste mali občas problém s prechodom medzi rovnostranným a všeobecným trojuholníkom. V rovnostrannom sú napríklad ťažnice zároveň výškami a tak ste sa snažili pracovať s výškami miesto ťažníc aj v obecnom prípade. To však nechávalo práve ťažisko ako neoverenú možnosť.

S celými a desatinnými časťami premenných sa dosť ťažko pracuje, preto by sme sa ich radi nejak zbavili. To môžeme urobiť napríklad tak, že sčítame celú a desatinnú časť nejakej premennej, vtedy totiž dostaneme pôvodnú premennú. Keďže každá premenná sa nachádza v sústave raz ako celá časť a raz ako desatinná časť, stačí nám sčítať všetky rovnice (súčet ich ľavých strán bude rovnaký ako súčet ich pravých strán). Tým dostaneme:

x + \left\lfloor{x}\right\rfloor + \{x\} + y + \left\lfloor{y}\right\rfloor + \{y\} + z + \left\lfloor{z}\right\rfloor + \{z\} = 6{,}6\\2(x + y + z) = 6{,}6\\x + y + z = 3{,}3

Ďalšie informácie môžeme získať z toho, že sčítame iba niektoré dvojice rovníc. Napríklad prvé dve:

x + y + z + \left\lfloor{y}\right\rfloor + \{x\} = 3{,}3\\\left\lfloor{y}\right\rfloor + \{x\} = 0

Využili sme pri tom, že x + y + z = 3{,}3 a toto odčítali od oboch strán. Keďže však teraz naľavo máme iba súčet desatinnej a celej časti, tak \left\lfloor{y}\right\rfloor musí byť práve celá časť a \{x\} práve desatinná časť pravej strany, čiže obe 0.

Môžeme pokračovať sčítavaním ďalších dvojíc rovníc. Zase vieme použiť podobný postup a vyjde nám celá a desatinná časť nejakých iných premenných. Z druhej a tretej rovnice máme:

x + y + z + \left\lfloor{z}\right\rfloor + \{y\} = 5{,}5\\\left\lfloor{z}\right\rfloor + \{y\} = 2{,}2

Takže \left\lfloor{z}\right\rfloor = 2 a \{y\} = 0{,}2. Nakoniec sčítame tretiu a prvú rovnicu:

x + y + z + \left\lfloor{x}\right\rfloor + \{z\} = 4{,}4\\\left\lfloor{x}\right\rfloor + \{z\} = 1{,}1

Takže \left\lfloor{x}\right\rfloor = 1 a \{z\} = 0{,}1. Teraz už máme všetko, čo potrebujeme, a vidíme, že riešenie je x = 1{,}0; y = 0{,}2; z = 2{,}1.

Komentár

Väčšina z vás úlohu riešila približne takto a zvládli ste to bez problémov. Bolo aj zopár riešení, kde ste rozoberali viacero rôznych prípadov, ktoré mohli nastať, tam ale treba dávať pozor, aby ste naozaj skúsili všetky možnosti. Inak na to, že to bol deviaty príklad, tak riešení bolo veľmi veľa a väčšina úplne správnych, takže ste šikovní :)

Najprv si objasnime zopár vlastností postupnosti f:

1. Všetky členy postupnosti f sú kladné. Platí to preto, lebo sú kladné prvé dva, a každý ďalší je len súčtom nejakých predošlých.
2. Postupnosť f rastie. Inak povedané, každý člen postupnosti f je nižší ako nasledovný. Pre prvý člen f_1​ to očividne platí: 2 \lt 3. Pre akýkoľvek ďalší člen f_i to platí, pretože zo zadania vieme, že f_{i+1} = f_i + f_{i-1}, teda že nasledovný člen je súčtom f_i a nejakého iného členu f_{i-1}​. Ako už vieme, každý člen je kladný, vrátane f_{i-1}​. Preto nasledovný člen f_{i+1} je určite vyšší ako f_i.
3. Ľubovoľný člen postupnosti f je vyšší než polovica nasledujúceho členu. Opäť to očividne platí pre prvý člen: 2 je naozaj viac než polovica z 3. Dôkaz pre vyššie členy vieme dostať z toho, že postupnosť rastie. Vezmeme nerovnosť f_i \gt f_{i-1} a postupne ju upravíme. Pripočítajme k obom stranám f_i, čím dostaneme 2\cdot f_i \gt f_i + f_{i-1}. Vidíme, že na pravej strane dostávame veľkosť členu f_{i+1}, tak ju ním nahraďme: 2\cdot f_i = f_{i+1}. Teraz už len obe strany vydelíme dvomi a máme f_i \gt \frac{f_{i+1}}{2}, čo je náš želaný výsledok.​

Teraz môžeme dokončiť riešenie. Ak niekedy dostaneme nulu, tak to bude určite hneď v prvom kroku. Prečo to nemôže nastať neskôr? Predstavme si, že prvý krok už prebehol. Teda číslo, ktoré momentálne máme, je nejaký kladný násobok nejakého f_i. Teda naše číslo je určite rovné aspoň f_i​. Na to, aby sme ho teraz nahradili nulou, musela by byť nula najbližším násobkom f_{i+1} (alebo aspoň na zdieľanom prvom mieste, teda rovnako blízko, ako nejaký iný násobok). Ale my vieme, že každý člen f_i je vyšší než polovica f_{i+1}. Naše číslo je určite aspoň také veľké ako tento člen, preto tiež musí byť vyššie než táto polovica, a teda je určite bližšie k f_{i+1}​ ako k nule. Preto sa určite nemôže stať, že nula by bola najbližším násobkom f_{i+1}.

Ostáva nám už iba zistiť, ktoré počiatočné n sa hneď v prvom kroku zmenia na 0. f_1 je rovné 2, teda hľadáme nejaké také číslo, že je rovné najviac polovici z 2 (platí rovnaká logika ako pred chvíľou, ak je naše číslo vyššie než polovica nasledovného členu, určite nebude nula jeho najbližším násobkom...). Jediné také číslo je 1, a naozaj, pre neho si ľahko overiť, že sa hneď zmení na nulu.

Odpoveď: Jediným vyhovujúcim číslom n je 1.​