Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×1. príklad
Zadanie
Vzorové riešenie
Označme si hmotnosti ingrediencií veľkými písmenami a hmotnosti obsahov šálok malými písmenami:
Š = špagety \\ K = klobásky \\ S = syr \\ č = červená \\ z = zelená \\ m = modrá
Zo zadania poznáme nasledovné rovnice:
z = K + 1202 \\ m = S - 2021 \\ č = Š + ?
Vidíme, že obsah zelenej šálky váži viac ako klobásky, obsah modrej šálky váži menej ako syr, a obsah červenej šálky váži viac ako špagety. To znamená, že v zelenej šálke nemôžu byť klobásky, v modrej šálke nemôže byť syr a v červenej šálke nemôžu byť špagety. Pozrime sa, aké sú všetky možnosti, ako môžu byť v šálkach ingrediencie rozmiestnené podľa toho, kde sú špagety:
1. Špagety môžu byť v modrej šálke. Pokiaľ je to tak, klobásky nemôžu byť ani v zelenej, ani v modrej šálke, a teda musí byť v červenej. Dve zo šálok sú už obsadené, teda syr musí byť v poslednej voľnej zelenej šálke.
Š = m \\ K = č \\ S = z
Môžeme si za hmotnosti šálok v rovniciach dosadiť hodnoty ich obsahov:S = K + 1202 \\ Š = S - 2021
Vidíme, že syr je o 1202 ťažší ako klobásky, a špagety sú o 2021 ľahšie ako syr. Teda vieme aj, o koľko sú špagety ľahšie ako klobásky:Š = S - 2021 = K + 1202 - 2021 = K - 819
Klobásky sú v červenej šálke, teda vidíme, že obsah červenej šálky je o 819 gramov ťažší ako špagety.
2. Špagety môžu byť v zelenej šálke. Pokiaľ je to tak, syr nemôže byť ani v modrej, ani v zelenej šálke, a teda musí byť v červenej. Dve zo šálok sú už obsadené, teda klobásky musia byť v poslednej voľnej modrej šálke.
Š = z \\ S = č \\ K = m
Dosadíme hmotnosti ingrediencií za hmotnosti šálok do rovníc zo zadania:
Š = K + 1202 \\ K = S - 2021
Vidíme, o koľko sú špagety ťažšie ako klobásky, a o koľko sú klobásky ľahšie ako syr, tak vypočítame, o koľko sú špagety ľahšie ako syr:Š = K + 1202 = S - 2021 + 1202 = S - 819
Keďže syr je v červenej šálke, obsah červenej šálky je o 819 gramov ťažší ako špagety.
Odpoveď: V červenej šálke je určite o 819 gramov ingrediencie viac, ako v šálke so špagetami.
Komentár
Najčastejšou chybou bolo, že ste vyskúšali vo svojom riešení iba jednu možnosť, ako mohli byť v šálkach jednotlivé ingrediencie usporiadané. Riešení totiž môžeme mať viac a treba overiť, že naozaj máme všetky.
2. príklad
Zadanie
Poznámka: Značenie n! znamená súčin všetkých čísel od 1 po n. Napríklad: 4! = 4\cdot 3\cdot 2\cdot 1=24
Vzorové riešenie
Najprv sa pozrime na to, ktoré cifry môžeme v našom čísle \overline{ABC} použiť:
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40360
9! = 362880
Ako si môžeme vštimnúť, tak cifry od 7 do 9 použiť nemôžeme, pretože inak by bolo výsledné číslo 4 alebo viac ciferné. Rovnako vieme vyradiť aj cifru 6. 6! je 720, teda v súčte faktoriálov budeme mať na mieste stoviek určite cifru 7 alebo väčšiu. Toto ale nemôže nastať, ako sme si ukázali vyššie.
Aký najvyšší súčet faktoriálov vieme dostať, ak by sme v čísle nepoužili 5? Najväčšia cifra, ktorú ešte môžeme použiť je 4, avšak súčet 4! + 4! + 4! je len 72, čo je dvojciferné číslo. Teda vieme, že v našom hľadanom čísle bude aspoň jedna cifra 5.
Skúsme zistiť, koľko cifier 5 sa môže nachádzať v hľadanom čísle. Ak by sa v čísle nachádzali 3 cifry 5, tak súčet 5! + 5! + 5! vychádza 360, čo nevyhovuje zadaniu.
Ak by sa v čísle nachádzali 2 cifry 5, tak súčet faktoriálov vyzerá zatiaľ nasledovne 5! + 5! = 240. Ak teraz pripočítame k výsledku ľubovoľný faktoriál (okrem 5!, čo sme si ukázali vyššie), tak sa cifra 2 na mieste stoviek už nezmení.Teda ak sa v čísle nachádzajú 2 cifry 5, tak sa tam určíte nachádza aj cifra 2 na mieste stoviek. Ale súčet 2! + 5! + 5! = 242 nie je 255, teda táto možnosť nevyhovuje.
Teda v hľadanom čísle sa nachádza práve jedna cifra 5. Najväčší súčet faktoriálov dosteneme, ak použijeme cifry 5, 4 a 4. Súčet ich faktoriálov je ale 120 + 24 + 24 = 168, teda hľadané číslo určite začína cifrou 1.
Teraz nám stačí už len doskúšať zostávajúce 4 možnosti:
1! + 1! + 5! = 122 - nesedí
1! + 2! + 5! = 123 - nesedí
1! + 3! + 5! = 127 - nesedí
1! + 4! + 5! = 145 - sedí!
Odpoveď: Jediné číslo vyhovujúce zadaniu je 145.
3. príklad
Zadanie
- Priemerná hmotnosť troch najťažších šálok je práve hmotnosťou jednej z nich.
- Priemerná hmotnosť štyroch najťažších šálok je práve hmotnosťou jednej z nich.
- Priemerná hmotnosť všetkých piatich šálok je práve hmotnosť jednej z nich.
- Druhá najťažšia šálka váži o 16 gramov viac ako druhá najľahšia z nich.
Vzorové riešenie
Keď sa pozrieme na príklad, tak zadanie nám hovorí tvrdenia o priemeroch hmotností piatich šálok. Hmotnosti samotných šálok nepoznáme, tak väčšinou sa s neznámymi číselnými hodnotami dobre zachádza, keď si ich označíme písmenkami. Napríklad si teda šálky vieme označiť ako A, B, C, D a E, pričom šálka A je najťažšia a šálka E najľahšia.
Ďalej si v zadaní vieme všimnúť 4 informácie, tak poďme si ich postupne rozobrať:
Priemerná hmotnosť troch najťažších šálok je hmotnosťou jednej z nich.
Keďže priemerná hmotnosť šálky A je A a pridaním dvoch ľahších šálok sa zníži, tak bude určite priemerná hmotnosť šálok A, B a C nižšia ako A. Podobne priemerná hmotnosť šálky C je C a pridaním šálky A a B sa zvýši. Preto ak je priemer 3 najväčších hodnôt váhou nejakej šálky, tak to bude práve B. Tiež je dobré si uvedomiť, že hmotnosti A a C musia byť od B rovnako vzdialené. Vieme to získať napríklad jednoduchým výpočtom. Aritmetický priemer troch hodnôt dostávame ako \dfrac{A+B+C}{3}. Táto hodnota sa má rovnať B, tak ich položme rovné a úpravamy postupne dostávame:A+B+C=3B \\ A+C=2B \\ A-B=B-C
Toto nám však hovorí, že šálka A ja od šálky B vzdialená rovnako ako šálka C, čo sme presne chceli. Nazvyme si túto vzdialenosť X.Priemerná hmotnosť štyroch najťažších šálok je jednou z nich.
Priemerná hmotnosť sa pridaním šálky s podpriemernou hmotnosťou zníži. Takže priemer štyroch najťažších šálok musí byť nižší ako B. No a určite si ľahko domyslíte, že to nemôže byť hmotnosť najľahšej šálky D. Ostáva nám teda šálka C. Potom aritmetický priemer štyroch najťažších šálok je \dfrac{A+B+C+D}{4}. Dostávame teda:A+B+C+D=4C \\ A+B+D=3C \\ A-C + B - C=C-D
V normálnej reči A-C značí o koľko je šálka A ťažšia od šálky C, to si podobne ako v jednotke môžeme zaznačiť na číselnú os. Rovnako si zaznačíme vzdialenosti bodov B, C a C, D. Vieme, že súčet prvých dvoch vzdialeností je rovnaký ako tá tretia, ktorú nazvyme Y. Potom si môžeme všimnúť, že Y = 3 X. Viď obrázok.
Vzdialenosť A od C je 2X a vzdialenosť B od C je X, čo nám dáva už spomínanú rovnosť. Zároveň máme v obrázku zaznačenú aj informáciu, že rozdiel medzi druhou najťažšou a najľahšou šálkou je 16 gramov.
Priemerná hmotnosť piatich najťažších šálok je jednou z nich.
Pridaním šálky E sa priemerná hmotnosť znovu zníži, teda ich priemerom nemôže byť šálka ťažšia ako predchádzajúci priemer, ktorý bol C. Rovnako však priemerom piatich šálok s rozličnou hmotnosťou nemôže byť šálka ktorá je z nich najľahšia. Ostáva nám teda jediná možnosť, ktorou je šálka D. Priemer všetkých piatich šálok vyrátame ako \dfrac{A+B+C+D+E}{5}. Z čoho dostávame rovnosť:\displaystyle\dfrac{A+B+C+D+E}{5}=D \\ A+B+C+D+E=5D \\ A+B+C+E=4D \\ A-D + B - D + C-D = D-E
Opäť dostávame rovnosti súčtov vzdialeností, ktoré môžeme zaznačiť na číselnej ose, pričom vzdialenosť D-E si označme Z.Potom Z vieme dostať ako: X + X + 3X - vzdialenosť A od D, zväčšená o X + 3X - vzdialenosť B od D, no a to ešte musíme zväčšiť o vzdialenosť C a D, ktorá je 3X. Dostávame teda: Z = X + X + 3X + X + 3X + 3X = 12X.
Z obrázku však rýchlo vidíme, že X + 3X = 16, preto X sú 4 gramy a vzdialenosť medzi A a E je X + X + 3X + 12X = 17X. Takže vzdialenosť A a E je 4 \cdot 17 = 68 gramov.

Komentár
Ahojte, príklad ste riešili veľmi pekne väčšinou pomocou priamočiarejšieho dosadenia a úprav rovníc. Zásadné problémy neboli, len si treba dať pozor, že tvrdenia, ktoré sa vám zdajú jasné, ako napríklad, že priemer troch najťažších šálok bude tá stredná, nemusia byť jasné všetkým a teda to treba poriadne zdôvodniť. Prajeme veľa radosti pri ďalšom riešení.
4. príklad
Zadanie
Koľko najmenej vriec musí ešte zo svojich vreciek bez pozerania sa vytiahnuť, aby malo istotu, že bude mať dve vrecia s rovnakým číslom, ak videlo na začiatku vrecia s číslami 262 a 663?
A koľko ich bude musieť ešte vytiahnuť ak vrecia mali čísla 101 a 102? Koľko z nich môže v tomto prípade vytiahnuť z ľavého vrecka, aby stále vytiahlo dokopy minimálny počet vriec, ale ostala mu istota, že dve vrecia budú mať rovnaké číslo? Nájdite všetky možnosti.
Poznámka: Číslo je deliteľné tromi práve vtedy, ak je aj jeho ciferný súčet deliteľný tromi.
Vzorové riešenie
Najprv zistíme, koľko vriec je v pravom vrecku, koľko vriec je v ľavom vrecku a koľko je vriec takých, že ich číslo sa nachádza v obidvoch vreckách.
Ľavé vrecko
Všetkých trojciferných čísel je 900 (999 číslel menších ako 1000, no 99 z nich má len jednu alebo dve cifry). Keďže každé tretie číslo z nich je deliteľné tromi teda bude 900 \div 3 = 300 čísel, ktoré sú trojciferné aj deliteľné tromi. V ľavom vrecku je teda 300 vriec.
Pravé vrecko
V pravom vrecku sú všetky trojciferné čísla, ktoré majú práve dve rovnaké cifry. Tie si označme A, a zvyšnú cifru si označme B. Potom môže číslo v pravom vrecku byť AAB, ABA alebo BAA. Vo všetkých troch prípadoch na mieste stoviek môžu byť cifry od 1 po 9 (nula nemôže byť na začiatku trociferného čísla) a druhá cifra (B, alebo v treťom prípade A) môže byť od 0 po 9, okrem tej z nich, ktorá je už na mieste stoviek, pretože nemôžu byť všetky tri cifry rovnaké. Dokopy vieme teda pre každý z troch prípadov vybrať 9 rôznych cifier na začiatok, a potom ešte raz 9 rôznych cifier. To znamená, že celkovo je 3 \cdot 9 \cdot 9 = 243 vriec v pravom vrecku.
Obe vrecká
Na to aby sa vrece nachádzalo v oboch vreckách musí byť deliteľné tromi a mať práve dve rovnaké cifry. Pre každú dvojicu rovnakých cifier teda skúsime doplniť tretiu cifru tak, aby ich ciferný súčet bol deliteľný tromi, čo zaručí že aj celé číslo bude deliteľné tromi:
| 11 | 4,7 |
|---|---|
| 22 | 5,8 |
| 33 | 0,6,9 |
| 44 | 1,7 |
| 55 | 2,8 |
| 66 | 0,3,9 |
| 77 | 1,4 |
| 88 | 2,5 |
| 99 | 0,3,6 |
| 00 | 3,6,9 |
Dokopy teda máme 24 kombinácii, pričom v každej môžeme tretiu cifru umiestniť na jedno z troch miest. Výnimkou sú čísla s dvomi nulami, kde musí byť pridaná cifra na začiatku, a čísla s jednou nulou, ktorá môže ísť iba na dve miesta. Máme teda dokopy 18 \cdot 3+3 \cdot 2+3 \cdot 1 = 63 čísel ktoré sú v oboch vreckách.
Prvý prípad
V prvom prípade máme vybrané vrecia s číslami 262 a 663. Keďže 262 nie je deliteľné tromi, tak nemôže byť z ľavého vrecka a teda musí byť z pravého vrecka. 663 je z iného vrecka a teda musí byť z ľavého. 663 má aj dve rovnaké cifry, teda ho môžeme vytiahnuť aj z pravého vrecka.
Keď chceme mať istotu, že vytiahneme 663 z pravého vrecka, tak musíme vytiahnuť všetky čísla, lebo 663 by sme mohli vytiahnuť ako posledné. Čiže spolu vytiahneme 242 čísel, lebo na začiatku už bolo jedno, 262, vytiahnuté. Ak by sme chceli použiť aj ľavé vrecko, museli by sme vytiahnuť všetky čísla ktoré sa nenachádzajú v pravom, aby sme potom mali istotu že vytiahneme aj nejaké užitočné. Stále to ale platí aj pre pravé vrecko, pretože z neho ešte spoločné číslo nemáme. Dokopy by to bolo 300 - 63 = 237 a 242 - 63 = 179 vytiahnutí, čo je jednoznačne viac ako naše riešenie s 242 vytiahnutiami.
Druhý prípad
V druhom prípade máme vybrané vrecia s číslami 101 a 102. 101 má dve rovnaké cifry a nie je deliteľné tromi, takže je z pravého vrecka a nemôžem ho vytiahnuť z ľavého vrecka. 102 nemá dve rovnaké cifry ale je deliteľné tromi takže je z ľavého vrecka a nemôžem ho vytiahnuť z pravého vrecka. V pravom vrecku ostáva 242 čísel a v ľavom vrecku ostáva 299 čísel.
Aby sme mali istotu, že vytiahneme z pravého vrecka číslo, ktoré sa nachádza aj v ľavom vrecku, musíme rátať s tým, že sme najskôr vytiahli všetky čísla ktoré sa nachádzajú iba v pravom vrecku. To isté platí opačne pre ľavé vrecko. Z pravého vrecka musíme vytiahnuť ešte 242 - 63 = 179 a z ľavého 299 - 63 = 236 čísel, aby sme mali istotu, že ďalšie vytiahneme nejaké číslo, ktoré sa nachádza v oboch vreckách. Teraz máme rovnakých 63 čísel v oboch vreckách.
Aby sme mali istotu, že vytiahneme dve rovnaké čísla, musíme vytiahnuť aspoň o jedno číslo viac ako je počet rôznych čísel, inak by sme mohli každé číslo vytiahnuť práve raz, bez ohľadu na to z ktorého by sme ťahali, keďže všetky sú v oboch. Takže ešte musíme vytiahnuť ešte 64 čísel. Tieto čísla môžeme vyťahovať z vriec ľubovoľne, lebo stále bude platiť, že 64-té číslo už musí byť rovnaké ako niektoré pred tým, keďže rôzne čísla sa už minuli.. Dokopy sme vytiahli 179 + 236 + 64 = 479 čísel. Z ľavého vrecka mohlo byť 236 + (1 až 63) = 236, 237,…,299.
Odpoveď: V prvom prípade musí vybrať aspoň 242 vriec. V druhom ich musí vybrať 479, pričom z ľavého vreca môže vytiahnuť 237 až 299.
Komentár
Väčšina riešiteľov šikovne zvládlo vysvetliť, akou stratégiou treba čísla z vriec vyberať, takže aj v prípade, že došlo k chybe pri zisťovaní počtov čísel vo vreciach, získali slušný počet bodov.
Pri tomto počítaní jednotlivých skupín čísel sa však často stávalo, že sme nevedeli skontrolovať ako riešiteľ skúšal všetky možnosti pre dané čísla, pretože ich nevypísal, čo určite treba robiť. Vynechať pri vypisovaní môžeme nanajvýš jednokrokové očividné operácie ako sčítavanie, napríklad v tomto vzorovom riešení v tabuľke, kde nevypisujeme súčty ktoré majú byť deiteľné tromi.
Pri počte čísel v oboch vreciach sa tiež mohlo stať, že riešiteľovi vyšiel správny výsledok, no nezarátal tri čísla s dvomi nulami, ale zarátal ostatné čísla s nulou na začiatku.
Náročná sa však ukázala hlavne tretia podotázka, na ktorú pomerne veľa riešiteľov vôbec neodpovedalo, a po prvom nájdenom riešení druhej možnosti už nezisťovali, či nemôžeme vyťahovať inak, aby sme dosiahli rovnaký počet 479.
5. príklad
Zadanie
Vzorové riešenie
Je 10 porotcov a každý pozná porotcu vo svojej dvojici. Porotca si sám so sebou ruku nepodáva a ani s porotcom vo dvojici, keďže ho pozná. Preto si porotca môže podať ruku s najviac 8 porotcami (keď nepozná nikoho okrem porotcu vo dvojici). Najmenej si môže porotca podať ruku s 0 porotcami (keď pozná všetkých porotcov).
Mišo si všimol, že každý z ostatných 9 porotcov si podal ruku s iným počtom porotcov. Títo porotcovia majú zároveň 9 možností na to, s koľkými porotcami si môžu podať ruku, a to od 0 do 8. Jeden z porotcov si teda musel podať ruku s 0 porotcami, jeden z porotcov si musel podať ruku s 1 porotcom, a tak ďalej, až posledný porotca si musel podať ruku s 8 porotcami.
Označme si porotcu, ktorý si podal ruku s 0 porotcami P_0, porotcu, ktorý si podal ruku s 1 porotcom P_1, a tak ďalej, až porotcu, ktorý si podal ruku s 8 porotcami P_8 (jeden z týchto porotcov je Paľo, zatiaľ však nevieme ktorý).
Porotca P_8 si musel podať ruku so všetkými porotcami okrem svojej dvojice. Jediný porotca, ktorý si ešte nepodal ruku je porotca vo dvojici s P_8. Tento porotca musí byť preto P_0 (nikto iný to nemôže byť). Z toho vyplýva, že porotca P_8 musí byť vo dvojici s P_0.

Porotca P_7 si potom musel podať ruku so všetkými okrem P_0 (ten si s nikým nepodal ruku) a porotcu vo svojej dvojici. Všetci porotcovia, okrem P_0 a porotcu vo dvojici s P_7, si už podali ruku aspoň 2-krát. Jediný, kto môže byť P_1 je teda porotca vo dvojici s P_7. Porotcovia P_7 a P_1 sú teda vo dvojici.

Porotca P_6 si už nemôže podať ruku s P_0 ani s P_1, ani s porotcom, ktorý je s ním vo dvojici. Preto si musí podať ruku so všetkými ostatnými porotcami. Potom všetci porotcovia, okrem P_0, P_1 a porotcu vo dvojici s P_6, si podali ruku aspoň 3-krát. Porotca vo dvojici s P_6 teda musí byť P_2.

Porotcovia P_0, P_1, P_2 už majú vyčerpaný počet podaní rúk, preto si s nimi P_5 nemôže podať ruku. Porotca P_5 si preto musí podať ruku so všetkými okrem P_0, P_1, P_2 a svojej dvojice. Všetci porotcovia, okrem P_0, P_1, P_2 a porotcu vo dvojici s P_5 si podali ruku aspoň 4-krát. Tým pádom porotca vo dvojici s P_5 musí byť P_3.

Z toho vyplýva, že porotcovia prišli vo dvojiciach (P_0, P_8), (P_1, P_7), (P_2, P_6), (P_3, P_5). Zostávajú nám už iba porotcovia P_4 a Mišo. Títo dvaja musia teda byť spolu vo dvojici. Keďže vieme, že Mišo je vo dvojici s Paľom, tak P_4 musí byť Paľo. Tým pádom si Paľo podal ruku so \mathbf{4} ľuďmi.
Komentár
V tejto úlohe bolo dôležité nielen zistiť, v ktorých dvojiciach porotcovia prišli a kto si s kým podal ruku, ale aj to poriadne dokázať. Aj keď väčšina z vás sa dopracovala k správnemu výsledku, viacerí ste práve pri dokazovaní neukázali, že toto riešenie je jediné možné. Na toto si v budúcnosti treba dať pozor.
6. príklad
Zadanie
Takto sa odohralo niekoľko hier, pričom tím penne vyhral 25 hier, tím fusilli vyhral 37 hier a tím quadretti vyhral 29 hier. Pre každú dvojicu tímov určite, koľko zápasov odohrali proti sebe, ak vieme že posledný zápas prehrali quadretti.
Vzorové riešenie
V každom zápase jeden tím vyhrá, jeden prehrá a jeden strieda. Zo zadania vieme, koľkokrát ktorý tím vyhral a chceli by sme zistiť, koľkokrát hrala proti sebe každá dvojica. Keď proti sebe hrá dvojica tímov, tak ten tretí tím vtedy strieda, čiže nám stačí zistiť, koľkokrát ktorý tím striedal.
Striedanie funguje tak, že práve vtedy, keď nejaký tím prehrá, pri ďalšom zápase strieda. Každý tím má teda rovnako veľa prehier ako striedaní. Výnimka je prvá a posledná hra, lebo quadretti v prvom zápase striedali, no predtým neprehrali, a v poslednom prehrali, no potom nestriedali. Majú teda navyše jednu prehru a jedno striedanie. To je ale rovnako veľa, takže stále platí, že každý tím má prehier rovnako veľa ako striedaní.
Teraz už nám stačí zistiť, koľkokrát každý tím prehral alebo striedal, a počet striedaní bude polovica z toho. No a tím prehrá alebo strieda vtedy, keď nevyhrá, čiže vtedy, keď vyhrá nejaký iný tím. Počet prehratí + striedaní jedného tímu teda bude súčet výhier zvyšných dvoch tímov.
Ostáva nám už len z toho, čo sme zistili, vypočítať odpoveď pre každý tím.
- Penne a fusilli spolu vyhrali 25 + 37 = 62 zápasov. Toľko zápasov teda prehrali alebo striedali quadretti. Striedanie z toho bola polovica, takže 62 : 2 = 31 zápasov. Penne a fusilli teda proti sebe hrali 31 zápasov.
- Penne a quadretti spolu vyhrali 25 + 29 = 54 zápasov. Toľko teda prehrali alebo striedali fusilli, z čoho 54 : 2 = 27 bolo striedaní. Penne a quadretti teda proti sebe hrali 27 zápasov.
- Fusilli a quadretti spolu vyhrali 37 + 29 = 66 zápasov. Toľko teda prehrali alebo striedali penne, z čoho 66 : 2 = 33 bolo striedaní. Fusilli a quadretti teda proti sebe hrali 33 zápasov.
Komentár
Veľa z vás úlohu riešilo tak, že ste si urobili konkrétny rozpis zápasov, kde najprv vyhrával stále jeden tím, potom druhý a nakoniec tretí, a jednoducho ste spočítali, koľkokrát proti sebe hrala každá dvojica. Z toho vám síce vyšiel správny výsledok, ale takéto riešenie fungovalo len pre to jedno konkrétne poradie. Zadanie pritom o poradí nič nehovorí, takže správne riešenie musí fungovať bez ohľadu na to, v akom poradí sa zápasy odohrali.
7. príklad
Zadanie

Vzorové riešenie
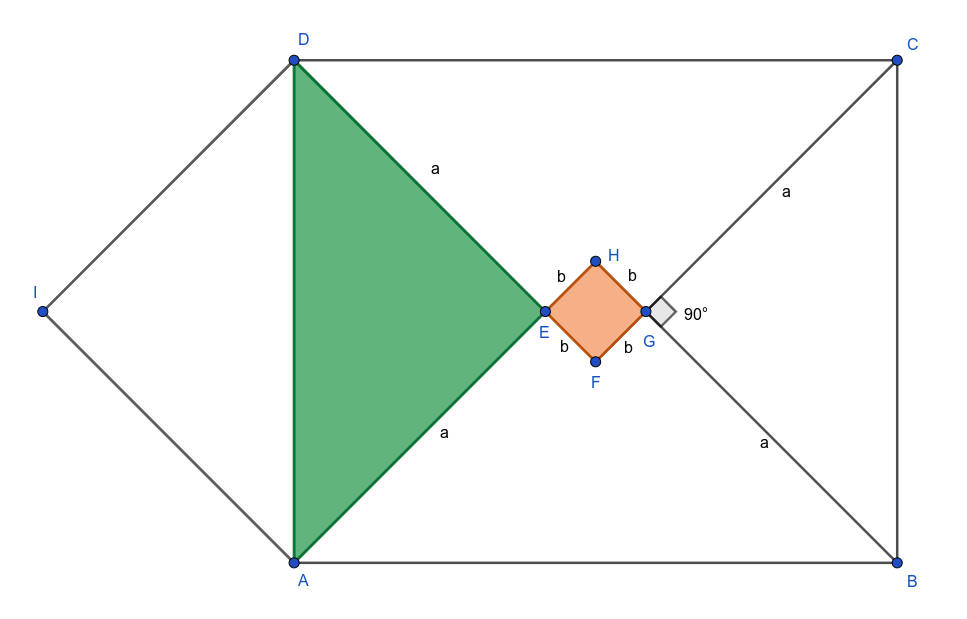
Najprv si dokážeme, že trojuholník AED a trojuholník BGC sú pravouhlé a rovnoramenné.
Uhol AED je vrcholový s uhlom HEF a uhol BGC je vrcholový s uhlom FGH, a teda sú oba pravouhlé. Označme si dĺžku strany štvorca b. Zo zadania vieme, že trojuholník DFC je rovnoramenný s dĺžkami ramien a+b, a aj trojuholník AHB je rovnoramenný s dĺžkami ramien a+b, teda platí, že |AE|=|DE|=|BG|=|CG|=|AH|-b označme si túto dĺžku a. Z toho vyplýva, že trojuholníky BGC a AED sú rovnoramenné.
Zo zadania vieme, že obsah zeleného trojuholníka AED je 50-krát väčší ako obsah oranžového štvorca FGHE. Ak by sme si zobrali štvorec AEDI, tak vieme, že je dvakrát väčší ako trojuholník AED a teda vieme povedať, že obsah štvorca AEDI je 100-krát väčší ako obsah štvorca FGHE.
Teraz si vyjadríme obsahy týchto štvorcov pomocou strán a a b.
S_{AEDI}=a^2=100\cdot S_{FGHE}=100\cdot b^2
a^2=100\cdot b^2
a=10 \cdot b
Mohli sme odmocniť, pretože obe dĺžky sú kladné čísla.
Strany AH a HB sú odvesnami rovnoramenného pravouhlého trojuholníka ABH a teda platí, že S_{AHB}=|AH|\cdot |HB|/2 . Dĺžky strán AH a BH si vieme taktiež napísať ako a+b .
Keďže vieme, že a = 10 \cdot b , tak dĺžky týchto strán sa budú rovnať 11\cdot b .
S_{AHB}=11\cdot b\cdot 11\cdot b/2
S_{AHB}=60{,}5b^2
Teraz si vieme vyjadriť obsah celého obdĺžnika pomocou dĺžky strany b:
2 \cdot S_{AED}+2\cdot S_{AHB}-S_{FGHE} = 990~\text{cm}^2 \\ 2\cdot 50\cdot b^2+2\cdot 60{,}5\cdot b^2-b^2 = 990~\text{cm}^2 \\ 221\cdot b^2-b^2 = 990~\text{cm}^2 \\ 220\cdot b^2 = 990~\text{cm}^2 \\ b^2 = 4{,}5~\text{cm}^2
Obsah bielej časti je teda:
990~\text{cm}^2 - S_{AED} - S_{FGHE}
990~\text{cm}^2 - 50b^2- b^2
990~\text{cm}^2 - 50\cdot4{,}5~\text{cm}^2 - 4{,}5~\text{cm}^2 = 760{,}5~\text{cm}^2
Odpoveď: Obsah bielej časti je 760{,}5~\text{cm}^2 .
8. príklad
Zadanie
Vzorové riešenie
Zoberme si situáciu kde najmenšie závažie nie je 1 . V tejto situácii dokážeme od každého závažia odčítať nejaké kladné celé číslo k , menšie ako najmenšie závažie. Toto môžeme spraviť, lebo pri každom porovnávaní máme na oboch stranách 2 závažia, takže od oboch strán odčítame hmotnosť 2k , čo nám nezmení výsledok porovnania. Nie len, že nám to nezmení porovnávania, ale aj nám to zmenší najväčšie závažie. My chceme zaistiť čo najmenšie najväčšie závažie, takže najmenšie závažie je 1 . Už vieme že najmenšie je 1 , tak druhé najmenšie bude 2 , lebo je to druhé najmenšie kladné celé číslo.
Aby to platilo pre ľubovoľnú štvoricu závaží, musí to platiť pre najhorší možný prípad. Tento prípad nastane keď budeme mať na jednej strane najťažšie závažie ( z ) s najlahším závažím (ktoré už vieme, že je 1 ), a na druhej strane druhé ( x ) a tretie ( y ) najťažšie závažia. Zo zadania vieme, že strana s najtažším závažím musí byt väčšia, tak si dajme túto situáciu do nerovnice.
x + y \lt z + 1
Keďže rátame s kladnými celými číslami tak najmenšie z , ktoré vyhovuje tejto nerovnici je x + y . To znamená, že najťažšie závažie musí byť súčtom druhého a tretieho najťažšieho závažia, druhé najťažšie súčtom tretieho a štvrtého najťažšieho, atď. Prípomína vám toto niečo? Áno, je to Fibonnaciho postupnosť!
Z tohoto si môžeme uvedomiť že i-te najlahšie závažie je i-ty člen Fibonnaciho postupnosti, pričom prvé dva členy sú 1 a 2 . Najťažšie závažie je vlastne 12-te najlahšie, čize 12-ty člen Fibonacciho postupnosti. Tento člen vieme zistiť napríklad tak, že si všetky členy do 12-teho vypíšeme.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
Odpoveď: Najmenšia hmotnosť najťažšieho zo všetkých závaží môže byť 233 .
Komentár
Skoro všetkým z vás chýbal riadny dôkaz na to, že najmenšie závažie je naozaj 1. Dalo by sa to považovať za chybu, ale rozhodli sme sa, že tentokrát za to nebudeme strhávať body, no dávajte si nabudúce pozor.
Tento dôkaz bol dôležitou súčasťou správneho riešenia, lebo síce teraz bolo správne riešenie zjavné ale nie vždy tak tomu je.
9. príklad
Zadanie
Vzorové riešenie
Riešenie bez obvodových uhlov

Začnime pozorovaním, že uhly \measuredangle ADB a \measuredangle DBC sú striedavé uhly, nakoľko sú AD a BC rovnobežky. Tieto dva uhly sú teda rovnako veľké a teda oba pravé. Potom platí, že kružnica opísaná trojuholníku BCD je Tálesova kružnica a jej stred (označíme S) bude ležať v strede prepony - úsečky CD.

Pri pohľade na obrázok si môžeme všimnúť, že trojuholník CDE vyzerá ako preklopený trojuholník DCB. Toto zdanie dokážeme. Vezmime si os úsečky CD a osovo súmerne cez ňu zobrazíme trojuholník DCB aj s jeho opísanou kružnicou. Táto os prechádza stredom CD, takže body C,\, D zobrazí navzájom jeden na druhý. Zároveň, keďže S leží na tejto priamke, kružnica sa zobrazí sama na seba. Zostáva nám ešte bod B. Jeho obraz bude ležať na priamke kolmej na našu os, v rovnakej vzdialenosti od osi ako bod B. Priamka AB je rovnobežná s CD a keďže tá je kolmá na našu os, bude aj AB. Miesto vzdialenosti využijeme opísanú kružnicu. Na nej leží bod B, takže jeho obraz bude ležať na preklopenej kružnici. To je ale tá istá kružnica. Obraz bodu B leží na priamke AB a kružnici opísanej DCB, takže to bude bod E.
Pozrime sa, čo nám to pomohlo. Trojuholníky DCB a CDE sú zhodné. Úsečky BC a DE sú teda rovnako dlhé. Navyše, ABCD je rovnobežník, čiže aj strany AD a BC majú rovnakú dĺžku. To však znamená, že trojuholník ADE je rovnoramenný. Pozrime sa na jeho uhly.
V rovnobežníku sú susedné uhly dokopy 180°, takže |\measuredangle EAD| = 180° - |\measuredangle ABC| = 180° - 115° = 65°. Keďže trojuholník ADE je rovnoramenný, aj |\measuredangle AED| = 65°. Tretí uhol dopočítame do 180°, vyjde 50° a máme výsledok.
Odpoveď: Uhol \measuredangle ADE má veľkosť 50°.
Iné riešenie bez obvodových uhlov
Začneme rovnako ako v prvom riešení. Uhly \measuredangle ADB a \measuredangle DBC sú striedavé, takže sú oba rovnaké. Trojuholník DCB je pravouhlý, takže podľa Tálesovej vety bude stred jeho opísanej kružnice ležať v strede strany CD. Tentokrát sa pozrime na úsečky spájajúce body B,\, C,\, D,\, E so stredom opísanej kružnice, bodom S.

Všetky ich dĺžky sú rovnako veľké, keďže sa jedná o polomer našej kružnice. Uvedomme si, že susedné uhly v rovnobežníku majú súčet veľkostí 180°. Takže |\measuredangle SCB| = 180° - 115° = 65°. Trojuholník BCS je rovnoramenný, takže aj |\measuredangle SBC| = 65°. Zvyšný uhol ich musí doplniť do 180°, takže |\measuredangle BSC| = 180° - 2 \cdot 65° = 50°.
Všimnime si, že teraz vieme dorátať uhly aj v susednom trojuholníku. Uhly \measuredangle SBC a \measuredangle SBE dávajú dokopy \measuredangle EBC, takže |\measuredangle SBE| = 115° - 65° = 50°. Uhol \measuredangle SEB bude rovnaký, keďže máme rovnoramenný trojuholník. Opäť dopočítame |\measuredangle BSE| = 180° - 2 \cdot 50° = 80°.
Prejdeme teraz k tretiemu rovnoramennému trojuholníku. Uhly \measuredangle DSE,\, \measuredangle BSE a \measuredangle BSC dávajú dokopy priamy uhol. Ich súčet teda bude 180°. Takže |\measuredangle DSE| = 180° - 50° - 80° = 50°. Zvyšné dva uhly musia byť rovnaké a vyjdú (180° - 50°) : 2 = 65°.
Na záver nám stačí uvedomiť si, že uhol \measuredangle SDE tvorí s uhlom \measuredangle ADE, ktorý nás zaujíma, uhol \measuredangle ADC. V rovnobežníku sú protiľahlé uhly rovnako veľké, takže dopočítame |\measuredangle ADE| = 115° - 65° = 50°.
Odpoveď: Uhol \measuredangle ADE má veľkosť 50°.
Riešenie s obvodovými uhlami
Na záver si ukážeme riešenie využívajúce trošku ťažšiu matematiku, konkrétne takzvané obvodové uhly. Ak máme na kružnici vyznačenú úsečku, tak platí, že nech si zvolíme ľubovoľný bod na jednom kružnicovom oblúku, tak po jeho spojení s bodmi úsečky dostaneme vždy ten istý uhol. Môžeme si všimnúť, že ak si ako našu úsečku zvolíme priemer kružnice, dostaneme Tálesovu vetu. Jediný rozdiel by bol v tom, že pri obvodových uhloch závisí na tom, na ktorej strane úsečky tretí bod zvolíme.

Prejdime teda k samotnému riešeniu. Podobne ako aj v zvyšných riešeniach začneme uhlami \measuredangle ADB a \measuredangle DBC. Tie sú striedavé a teda rovnako veľké. Platí teda |\measuredangle DCB| = 90°.
Pozrime sa teraz na úsečku DC (zelenú). Uhly \measuredangle DBC a \measuredangle DEC sú na tej istej strane kružnice, takže sú obvodové a rovnako veľké. Platí teda |\measuredangle DEC| = 90°.
Teraz musíme trochu zapremýšľať. Vieme dorátať uhly \measuredangle BAD a \measuredangle BCD. Keďže v rovnobežníku majú susedné uhly súčet 180°, budú oba 180° - |\measuredangle ABC| = 180° - 115° = 65°. V trojuholníku DCB tak vieme dorátať aj zvyšný uhol |\measuredangle BDC| = 180° - 90° - 65° = 25°. Ajhľa, opäť sme na obvode kružnice. Úsečke BC (modrá) prislúchajú obvodové uhly \measuredangle BDC aj \measuredangle BEC. Majú teda rovnakú veľkosť a |\measuredangle BEC| = 25°.
Teraz sme už blízko. Uhly \measuredangle AED,\, \measuredangle CED,\, \measuredangle BEC dávajú dokopy 180°. Dva z nich poznáme, dorátame |\measuredangle AED| = 180° - 90° - 25° = 65°. V trojuholníku ADE nám tak zostáva dopočítať |\measuredangle ADE| = 180° - 65° - 65° = 50°.
Odpoveď: Uhol \measuredangle ADE má veľkosť 50°.
Komentár
Napriek tomu, že Vašich riešení nebolo až tak veľa, postupy boli skutočne rôznorodé. Najpopulárnejší bol pravdepodobne postup podobný prvému vzorovému riešeniu. Tu sa tiež objavili najčastejšie chyby. Viacerí z Vás podcenili dôkaz faktu, že trojuholníky CDE a DCB sú naozaj osovo súmerné. Aj keď to na obrázku môže vyzerať jednoznačne, ten môže ľahko klamať. Vo všeobecnosti, ak máte pocit, že sú dva trojuholníky zhodné, je fajn zdôvodniť to poriadne.
10. príklad
Zadanie

Vzorové riešenie
Ako prvé sa pozrime na zadané obmedzenia usádzania (prvý obrázok vľavo). Presnejšie, všimnime si tri vyznačené zelené políčka. Na týchto políčkach taktiež nemôže sedieť porotca spolu s porotcom na žltom políčku, pretože potom by práve ten žltý zavadzal zelenému. Môžeme povedať, že každý porotca v skutočnosti obsadzuje nie päť, ale osem políčok. Presne tak, ako na pravom obrázku.

Uvedomme si teraz, že na ľubovoľných štyroch políčkach, ktoré tvoria rohy obdĺžnika s dvomi stĺpcami a tromi riadkami, môže sedieť nanajvýš jeden porotca. To preto, lebo každé z týchto políčok blokuje všetky tri ostatné (a možno aj ďalšie políčka, ale to nás teraz nezaujíma). To znamená, že vieme pokryť celú plochu niekoľkými takýmito skupinami napríklad tak, ako na nasledujúcom obrázku:

Na obrázku môžeme vidieť farebne a číselne naznačené tie spomínané rohy obdĺžnika. Nemusíme ani používať celú takúto formáciu, napríklad násobky päťky na pravom okraji používajú iba polovicu spomínaného obdĺžnika. Nakoniec spodný riadok tiež používa iba polovicu, ale tuto je jednoduchšie argumentovať, že viac ako päť porotcov sa do riadku nezmestí, keďže nemôžu sedieť vedľa seba.
Z tohto vyplýva, že viac ako 25 porotcov sa určite do mriežky nezmestí. Navyše, keď sa pozrieme na obrázok nižšie, tak vidíme, že práve 25 porotcov do mriežky usadiť vieme a to bez akéhokoľvek zavadzania si.

Odpoveď:
Najviac vieme usadiť 25 porotcov, napríklad tak, ako na poslednom obrázku.
Komentár
Tento príklad bol veľmi náročný a priemerný počet získaných bodov bol iba 3{,}136. Najväčší problém bol poriadny dôkaz toho, že viacej ako 25 porotcov usadiť nevieme. Veľakrát úplne chýbal, alebo bol nedostatočný - to, že je niečo najvýhodnejšie pre jeden riadok, ešte neznamená, že je to najlepšie pre celú tabuľku.
Na desaťbodový dôkaz treba uviesť niečo typu tohto vzorového riešenia, t.j. pokryť celú tabuľku tak, aby bolo jasné, prečo je práve 25 to najlepšie.
Prémia 1
Zadanie
Urobte to tak, aby malo čo najviac kúskov hlavnú príchuť modrú, a čo najmenej červenú. Hodnotí sa v prvom rade rozdiel týchto dvoch počtov. Ak budú mať dve riešenia tento rozdiel rovnaký, za lepšie považujeme to s väčším počtom takých kúskov, že hlavná príchuť v ňom má súčet čísel väčší ako súčet zvyšných dvoch príchutí v ňom.

Vzorové riešenie
Riešenie
Najvyšší dosiahnutý rozdiel bol 11 kúskov.
V tomto rozdelení bolo 7 červených, 20 žltých a 18 modrých.
Tento rozdiel bol dosiahnutý v nasledovnom riešení:

Komentár
Pre dosiahnutie čo najvyššieho rozdielu bolo najvýhodnejšie mať čo najmenej červených kúskov. Preto bolo vhodné začať priradením červených políčok s vysokou hodnotou do jedného kúsku, aby sme sa ich čo najefektívnejšie zbavili. Potom už len stačilo vytvoriť čo najviac modrých kúskov a zvyšok červených políčok priradiť tak, aby ich v čo najviac prípadoch prebila iná farba v danom kúsku.
Bodovanie
Vzhľadom na to, že výsledky boli rôzne, rozhodli sme sa, že druhé kritérium hodnotenia do úvahy brať nebudeme. Hodnotili sme čisto rozdiel modrých a červených kúskov.
- Rozdiel 11 - 8 bodov,
- rozdiel 10 - 7 bodov,
- rozdiel 9 - 6 bodov,
- rozdiel 8 - 5 bodov,
- rozdiel 5 až 7 - 4 body,
- rozdiel 2 až 4 - 3 body,
- rozdiel 0 až 1 - 2 body,
- rozdiel -4 až -1 - 1 bod,
- rozdiel -5 a menej - 0 bodov.



