Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

7. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Jakub Kuchár krája obdĺžnikové mäso na časti. Nad dlhšími stranami vykrojil dva prekrývajúce sa pravouhlé rovnoramenné trojuholníky, čím mäso rozdelil na 5 častí ako na obrázku. Obsah zeleného trojuholníka je 50 krát väčší ako obsah oranžového štvorca. Aký je obsah bielej časti, ak obsah celého obdĺžnika je 990 cm štvorcových?

Vzorové riešenie

Opravovali: Imro, Peter, šálka

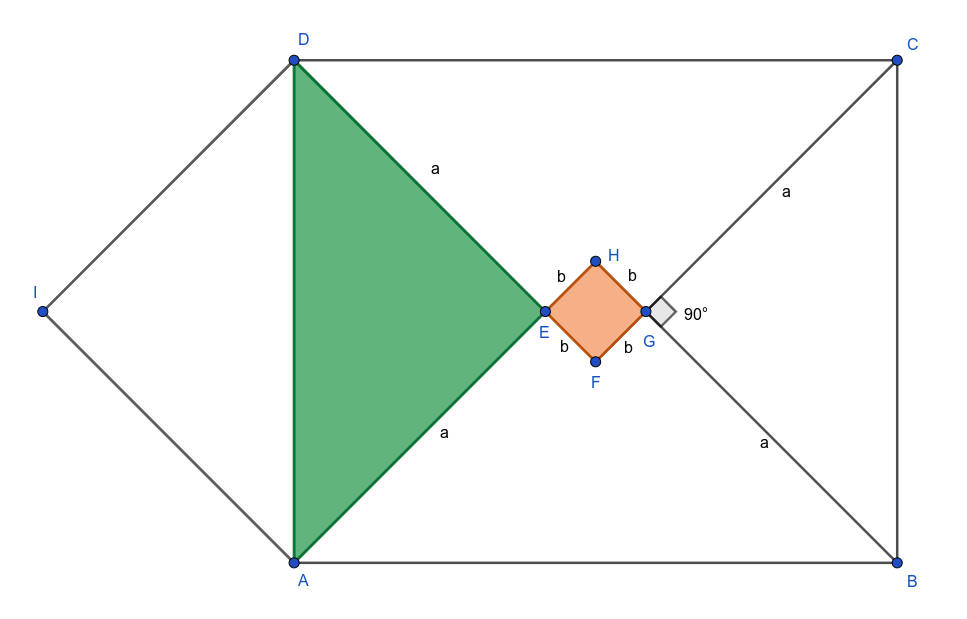
Najprv si dokážeme, že trojuholník AED a trojuholník BGC sú pravouhlé a rovnoramenné.

Uhol AED je vrcholový s uhlom HEF a uhol BGC je vrcholový s uhlom FGH, a teda sú oba pravouhlé. Označme si dĺžku strany štvorca b. Zo zadania vieme, že trojuholník DFC je rovnoramenný s dĺžkami ramien a+b, a aj trojuholník AHB je rovnoramenný s dĺžkami ramien a+b, teda platí, že |AE|=|DE|=|BG|=|CG|=|AH|-b označme si túto dĺžku a. Z toho vyplýva, že trojuholníky BGC a AED sú rovnoramenné.

Zo zadania vieme, že obsah zeleného trojuholníka AED je 50-krát väčší ako obsah oranžového štvorca FGHE. Ak by sme si zobrali štvorec AEDI, tak vieme, že je dvakrát väčší ako trojuholník AED a teda vieme povedať, že obsah štvorca AEDI je 100-krát väčší ako obsah štvorca FGHE.

Teraz si vyjadríme obsahy týchto štvorcov pomocou strán a a b.

S_{AEDI}=a^2=100\cdot S_{FGHE}=100\cdot b^2
a^2=100\cdot b^2
a=10 \cdot b

Mohli sme odmocniť, pretože obe dĺžky sú kladné čísla.

Strany AH a HB sú odvesnami rovnoramenného pravouhlého trojuholníka ABH a teda platí, že S_{AHB}=|AH|\cdot |HB|/2 . Dĺžky strán AH a BH si vieme taktiež napísať ako a+b .
Keďže vieme, že a = 10 \cdot b , tak dĺžky týchto strán sa budú rovnať 11\cdot b .

S_{AHB}=11\cdot b\cdot 11\cdot b/2
S_{AHB}=60{,}5b^2

Teraz si vieme vyjadriť obsah celého obdĺžnika pomocou dĺžky strany b:

2 \cdot S_{AED}+2\cdot S_{AHB}-S_{FGHE} = 990~\text{cm}^2 \\ 2\cdot 50\cdot b^2+2\cdot 60{,}5\cdot b^2-b^2 = 990~\text{cm}^2 \\ 221\cdot b^2-b^2 = 990~\text{cm}^2 \\ 220\cdot b^2 = 990~\text{cm}^2 \\ b^2 = 4{,}5~\text{cm}^2

Obsah bielej časti je teda:

990~\text{cm}^2 - S_{AED} - S_{FGHE}
990~\text{cm}^2 - 50b^2- b^2
990~\text{cm}^2 - 50\cdot4{,}5~\text{cm}^2 - 4{,}5~\text{cm}^2 = 760{,}5~\text{cm}^2

Odpoveď: Obsah bielej časti je 760{,}5~\text{cm}^2 .