Letný tábor 2025 - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×1. príklad
Zadanie
Vzorové riešenie
Na začiatku bolo v každej mise rovnako veľa polievky. Nazvyme si takéto množstvo polievky 1 porcia. Potom môžeme počítať, koľko polievky Anka postupne prelieva:
Anka preliala z prvej misy polovicu polievky do druhej. V prvej mise bola na začiatku 1 porcia polievky, takže Anka preliala \frac{1}{2} porcie. To znamená, že v prvej mise ostalo 1 - \frac{1}{2} = \frac{1}{2} porcie a v druhej bolo potom 1 + \frac{1}{2} = \frac{3}{2} porcie.
Anka preliala z druhej misy polovicu polievky do tretej. V druhej mise bolo predtým \frac{3}{2} porcie, takže Anka preliala \frac{\frac{3}{2}}{2} = \frac{3}{4} porcie. V tretej mise bolo potom 1 + \frac{3}{4} = \frac{7}{4} porcie.
Anka preliala z tretej misy polovicu polievky späť do prvej. V tretej mise je najprv \frac{7}{4} porcie, takže Anka preliala \frac{\frac{7}{4}}{2} = \frac{7}{8} porcie. Z prvej misy sme už ale polovicu odliali, teda v nej ostáva len \frac{1}{2} porcie, a teda po poslednom preliatí v nej ostáva \frac{1}{2} + \frac{7}{8} = \frac{11}{8}porcie.
V tretej mise bolo na konci \frac{11}{8} porcie, čo je o \frac{11}{8} - 1 = \frac{3}{8} porcie viac ako na začiatku. Teda platí, že 12 decilitrov sú \frac{3}{8} porcie, teda \frac{1}{8} porcie sú \frac{12}{3} = 4 decilitre, čiže jedna porcia je 4 \cdot 8 = 32 decilitrov. Na začiatku boli v misách tri porcie (v každej jedna), takže dokopy 32 \cdot 3 = 96 decilitrov. A keďže polievku sme z mís žiadnu neodliali preč, ani nepriliali novú, 96 decilitrov musí byť v misách aj teraz.
Odpoveď: Vo všetkých troch misách je dokopy 96 decilitrov polievky.
2. príklad
Zadanie
Vzorové riešenie
Vieme, že vždy, keď si z polievky naberieme 4 kúsky zeleniny, aspoň dva z nich budú rovnaké. Ak by v polievke boli štyri alebo viac rôznych druhov zeleniny, mohli by sme si nabrať po jednom kuse zo štyroch rôznych. To by nespĺňalo túto podmienku, takže vieme, že v polievke môžu byť najviac tri druhy zeleniny.
Teraz sa pozrime na druhú informáciu zo zadania. Keď si naberieme 5 kúskov zeleniny, vieme, že zo žiadneho druhu zeleniny nemôžeme nabrať viac ako tri kusy.
Čo ak by z nejakého druhu zeleniny boli v polievke aspoň 4 kusy? Potom by sme si vedeli nabrať takých päť kusov, že medzi nimi budú aj tieto štyri, a to nespĺňa podmienky zadania. V polievke teda nemôžu byť viac ako tri kusy zo žiadneho druhu zeleniny.
Vieme teda, že v polievke sú najviac tri druhy zeleniny, a z každého druhu sú v polievke najviac tri kusy. Taktiež ale vieme, že v polievke sa nachádza práve 9 kusov zeleniny. Pokiaľ by teda v polievke boli dva alebo menej druhov zeleniny, najviac by sme mohli v polievke mať 2 \cdot 3 = 6 kusov, čo nestačí. Druhy zeleniny musia byť práve tri. A vieme aj to, že z každého z týchto druhov musia byť v polievke práve 3 kusy, inak by sme mali v polievke spolu menej ako 3 \cdot 3 = 9 kusov zeleniny. Takže z kalerábu sú v polievke takisto 3 kusy.
Komentár
Pri takýchto úlohách je veľmi dôležité nielen prísť na správny výsledok, ale aj dokázať, že tento výsledok je jediný možný (alebo ak je možných výsledkov viac, nájsť všetky). Napriek tomu, že väčšina z vás mala správny výsledok, veľa z vás malo problém práve s touto časťou riešenia.
Vo všeobecnosti platí, že keď si prečítame vaše riešenie, malo by nám byť z neho jasné, prečo je toto riešenie správne, a prečo neexistuje žiadna iná správna odpoveď, ktorú ste nespomenuli.
Keď chcete dokázať, že niečo určite platí, častokrát to môžete spraviť takto: Predstavíte si, že by to neplatilo, a zisťujete, čo by z toho potom vyplývalo. Ak vám vyplynie niečo, čo si protirečí so zadaním, viete, že táto vec nemôže platiť.
Tento postup môže byť niekedy veľmi užitočný, preto sa oplatí vedieť, že sa to takto dá robiť. Ako vidíte, aj pri tejto úlohe sme ho využili hneď niekoľkokrát.
3. príklad
Zadanie
Vzorové riešenie
- nenakrájaná zelenina - N,
- zelenina nakrájaná na kolieska - K,
- zelenina nakrájaná na pásiky - P,
Najprv sa pokúsime zistiť, aké počty zelenín mal Ján pred chvíľou. Zapíšeme si podmienky zo zadania do rovníc:
N = K
7 \cdot N = P
N + K + P = 900
Za K si v poslednej rovnici teda môžeme dosadiť N a za P si môžeme dosadiť 7 \cdot N. Rovno túto rovnicu aj ďalej upravíme:
N + N + 7 \cdot N = 900
9 \cdot N = 900 ~~~~~~~~/{:}9
N = 100
Zistili sme teda, že nenakrájanej zeleniny bolo predtým 100 kusov, a podľa zvyšných dvoch rovníc vieme, že zeleniny nakrájanej na kolieska bolo tiež 100 a zeleniny nakrájanej na pásiky bolo 7 \cdot 100 = 700.
Teraz však Ján mohol hodiť časť nakrájanej zeleniny do hrnca alebo nakrájať časť nenakrájanej zeleniny na pásiky alebo kolieska, tak aby platili nové, iné podmienky pre N, K, P:
N = P
7 \cdot N = K
Keďže chceme zistiť, koľko najviac zeleniny mohlo mimo hrnca byť, zistíme, koľko najviac môže byť nenakrájanej zeleniny. Vidíme, že ostatné typy zeleniny vieme z jej počtu dopočítať. Dokonca platí, čím viac bude nenakrájanej zeleniny, tým viac bude aj zvyšných typov, a aj zostávajúcej zeleniny dokopy. Keby Ján iba krájal nenakrájanú zeleninu na kolieska, tak súčet počtov týchto dvoch typov ostane nezmenený, teda 100+100=200. To bude aj najvyšší možný súčet, pretože Ján nijak nevie pridať viac kusov zeleniny. Potom by platilo:
7 \cdot N = K a N + K = 200
N + 7 \cdot N = 200
8 \cdot N = 200
N = 25, K = 7 \cdot N = 7 \cdot 25 = 175
Keď si za K dosadíme 7 \cdot N a upravíme si rovnicu, dopracujeme sa k možnému počtu nenakrájanej zeleniny. Tento počet je najvyšší možný, pretože ak by sme mali viac nenakrájanej zeleniny, museli by sme mať, podľa zadania, viac aj tej na kolieska. Potom by sa však zvýšil aj súčet týchto dvoch typov, no ten sme už mali najvyšší možný.
Keďže pôvodne bolo zeleniny na pásiky 700, N = 25, a musí platiť N = P, tak Ján musí zahodiť 700 - 25 = 675 pásikov do hrnca. Takže mimo hrnca ostane N + K + P = 25 + 25 + 175 = 225 kusov zeleniny.
Odpoveď: Mimo hrnca môže byť najviac 225 kusov zeleniny.
Komentár
Väčšina riešiteľov, ktorí si vyjadrili v rovniciach počty zelenín už úspešne dospeli k správnemu riešeniu. Zopár riešiteľov dospelo aj k alternatívnemu riešeniu, kedy Ján nakrájal jednu nenakrájanú zeleninu na 593 koliesok. Vzhľadom na to, že sme zabudli v zadaní poriadne objasniť, že takéto niečo nemalo byť možné, rozhodli sme sa pri takomto postupe udeľovať body rovnako.
4. príklad
Zadanie
- Všemocná kuchárska kniha si myslí slovo zložené z piatich písmen, v ktorom sa žiadne písmeno neopakuje.
- Súťažiaci napíše nejaké slovo z piatich písmen.
- Všemocná kuchárska kniha odpovie dvoma číslami – prvé číslo udáva, koľko písmen napísaného slova sa zhoduje s mysleným slovom, t. j. stoja zároveň na správnom mieste; druhé číslo udáva, koľko písmen napísaného slova je obsiahnutých v myslenom slove, ale nestoja na správnom mieste.
- Kroky 2. a 3. sa opakujú, kým súťažiaci myslené slovo neuhádne.
| ATOLY | 1 | 1 |
| DOGMA | 0 | 2 |
| KMOTR | 0 | 4 |
| MUDRC | 0 | 2 |
| PLAST | 0 | 2 |
| SONET | 1 | 2 |
Vzorové riešenie
Začnime tým, že si pozrieme slovo KMOTR. Kniha nám o ňom povedala, že má 4 správne písmená, ale ani jedno nie je na správnom mieste. Takže vieme, že v myslenom slovo budú kombinácie písmen buď K,M,O,T alebo K,M,O,R alebo K,M,T,R alebo K,O,T,R alebo M,O,T,R.
Máme 5 možností, ktoré 4 písmená môžu byť vo výslednom slove. Poďme teda zistiť, ktorá z nich je tá správna.
Začnime kombináciou K,M,O,T. Predpokladajme, že všetky tieto písmená sú aj v slove. Poďme teda nájsť posledné písmeno. Zoberieme si slovo ATOLY. V ňom si vyznačíme správne písmená. Sú to O a T. Toto sedí aj s číslom, ktoré nám povedala kniha. Toto urobíme aj s ostatnými slovami. Pre slovo DOGMA to sedí, v slove MUDRC je ešte jedno písmeno okrem M správne, v slove PLAST aj SONET je tiež ešte jedno správne písmeno. Výsledné slovo je päťpísmenové, takže hľadáme jedno písmeno, ktoré sa nachádza v slovách MUDRC, SONET a PLAST. Takéto písmeno ale neexistuje, takže táto kombinácia písmen nie je správna.
Ďalej kombinácia K,M,O,R. Postupovať budeme rovnako ako doteraz. V slove ATOLY jedno správne písmeno ostalo, slovo DOGMA sedí, MUDRC sedí. V slovách PLAST aj SONET nám ostali 2 správne písmená. Keďže hľadané slovo má len 5 písmen, nemôžu sa v tých 2 slovách nachádzať až 2 ďalšie správne písmená. Inak by malo hľadané slovo až 6 písmen, čo nesedí so zadaním. Takže aj táto kombinácia je nesprávna.
Ďalšia je kombinácia K,M,T,R. Rovnaký postup aj tu. V slove ATOLY je ešte 1 písmeno správne. V slove DOGMA tiež a takisto v slove PLAST. V slove SONET sú ešte 2 písmená správne. Ako sme vysvetlili pri predošlej kombinácií, znamená to, že ani toto nie sú správne písmená.
Štvrtá kombinácia K,O,T,R. Slovo ATOLY sedí. V slovách DOGMA, MUDRC, PLAST, a SONET je v každom z nich ešte 1 správne písmeno. Aby výsledné slovo nemalo 6 písmen, musia mať tie 4 slová 1 spoločné. Také písmeno ale neexistuje. Takže táto možnosť tiež nie je správna.
Posledné treba vyskúšať písmená M,O,T,R. Slová ATOLY, DOGMA a MUDRC sedia. V slovách PLAST a SONET je ešte jedno správne písmeno. Toto písmeno musí byť v oboch slovách rovnaké, inak by hľadané slovo malo 6 písmen, čo nesedí so zadaním. V oboch slovách sa nachádza písmeno S. Takže písmeno S je posledné písmeno, ktoré sa nachádza v hľadanom slove.
Už vieme, že v hľadanom slove sa nachádzajú písmená M,O,T,R,S. Teraz ich treba správne zoradiť. Najprv zistíme pozície, kde sa písmená nemôžu nachádzať. Toto zistíme zo slov, ktoré majú 0 písmen na správnych pozíciach. Toto sú slová DOGMA, KMOTR a MUDRC.
- O nemôže byť 2. a 3.
- M nemôže byť 1. a 2.
- T nemôže byť 4. a 5.
- R nemôže byť 4. a 5.
- S nemôže byť 4.
Z tohto vieme, že v slove SONET nemôžu byť správne písmená O a T. Jediná ďalšie správne písmeno v tomto slove je S, takže S bude na 1. mieste. Ďalšie písmeno na správnom mieste je v slove ATOLY. Vieme, že O nemôže byť na 3. mieste, takže správne bude T, ktoré je na 2. mieste. Vieme, že R nemôže byť 4. a 5. Máme voľné iba 3 miesta, z toho na dvoch R nemôže byť, takže musí byť na tom poslednom voľnom, teda na 3. mieste. Ostavajú nám 2 miesta voľné. Vieme, že M nemôže byť 4., takže musí byť 5., lebo to jediné je voľné. Ostalo nám písmeno O, ktoré sa bude nachádzať na poslednom voľnom mieste, to jest na 4. mieste. Slovo, ktoré nám vyšlo je STROM.
Na konci ešte urobíme skúšku, aby sme si boli istý, že sme našli správny výsledok. Urobíme teda to isté, čo aj kniha v zadaní. Prvé číslo je počet správnych písmen na správnej pozícií, druhé číslo je počet správnych písmen na nesprávnych pozíciách.
| ATOLY | 1 | 1 |
| DOGMA | 0 | 2 |
| KMOTR | 0 | 4 |
| MUDRC | 0 | 2 |
| PLAST | 0 | 2 |
| SONET | 1 | 2 |
Toto sa zhoduje so zadaním, takže hľadané slovo je STROM.
Odpoveď: Kuchárska kniha si myslela slovo STROM.
Komentár
Skoro všetkým z vás chýbala skúška správnosti. Dalo by sa to považovať za chybu, ale rozhodli sme sa, že tentokrát za to nebudeme strhávať body, no dávajte si nabudúce pozor.
Prečo je skúška dôležitá? Skúška je na to, aby sme si overili, že riešenie, ktoré sme našli je správne. Môže sa stať, že úloha v skutočnosti nemá riešenie a to odhalíme práve vďaka skúške správnosti.
Tiež veľa z vás používalo zdôvodnenia, ako napríklad dané písmeno nemôže byť v slove, lebo sa nenachádza v ostatných slovách. Toto zdôvodnenie nie je správne, lebo to, že sa nejaké písmená nenachádza v iných slovách neznamená, že nebude v riešení. Napríklad, ak by v slove PLAST bolo K namiesto P, nič to na výsledku nezmení, aj keď bude písmeno K v dvoch slovách.
5. príklad
Zadanie
Vzorové riešenie
Štyri misky si označíme A, B, C, D. Rozdielne trojice misiek vieme dať ochutnať len štyrmi spôsobmi a to:
- A, B, C,
- A, B, D,
- A, C, D,
- B, C, D.
Ak by sme dali ochutnať niektorú trojicu znova, tak by nám mohol človek povedať vždy rovnakú odpoveď a teda potrebujeme zistiť, či vieme zistiť ktorá miska je aká, len pri týchto štyroch trojiciach misiek (ak by sa to nedalo, tak vieme, že sa to nebude dať ani pre konečný počet ochutnaní).
Všetkých možností na to, či je každá miska zo štyroch vydarená alebo pokazená je veľa (2\cdot2\cdot2\cdot2=16 možností). Keď k tomu ešte započítame, že sa mohol pri každom ochutnaní rozhodnúť klamať o rozličnej z 3 misiek, čo je za 4 kolá 81 kombinácií (3\cdot3\cdot3\cdot3=81), tak si rýchlo môžeme rozmyslieť, že sa ich nedá všetky vyskúšať.
Ako si teda vieme uľahčiť prácu? Najprv si vieme uvedomiť, že nás vlastne nezaujíma ktorá polievka je vydarená a ktorá pokazená. Zisťovať, či klame alebo hovorí pravdu vieme iba z toho, že niekedy zmenil svoju výpoveď. Takže pre každé klamanie nám to stačí overiť na konkrétnom príklade. Ďalej je nám jedno či sa raz zmenila informácia pri miske A, alebo D. Jednoducho misky vieme inak premenovať a dostaneme ten istý prípad. Takže nás zaujímajú počty klamaní a poradie v akom klamal, no stačí nám to vyriešiť iba pre jednu možnosť A, B, C, D. Nakoniec tiež je jedno poradie v ktorom misky ochutnávame, či najprv trojicu A, B, C a neskôr trojicu B, C, D alebo naopak. Vďaka tomu nám stačí vyriešiť iba 4 prípady, ktoré sú dané počtom zmien informácie, ktorý nám dá počet klamaní pri jednotlivých miskách.
Rozdelíme si koľkokrát mohol klamať o jednotlivých miskách:
- klamal raz o všetkých štyroch (1, 1, 1, 1) - vidíme 4 zmeny tvrdenia,
- klamal dvakrát o jednej, raz o dvoch a o poslednej neklamal (2, 1, 1, 0) - vidíme 3 zmeny,
- klamal dvakrát o dvoch miskách a o ostatných neklamal (2, 2, 0, 0) - vidíme 2 zmeny,
- klamal trikrát o jednej miske, raz o ďalšej a o ostatných neklamal (3, 1, 0, 0) - vidíme 1 zmenu.
Teraz si prejdeme všetky možnosti ako nám mohol klamať:
1. Klamal raz o všetkých štyroch
Pri všetkých štyroch polievkach budeme mať 2 rovnaké tvrdenia a práve jedno iné a teda budeme vedieť zistiť ktorá miska je aká. Klamať bude v tých ochutnaniach, ktoré sú iné.
(Červenou sú označené klamlivé tvrdenia.)
| miska A | miska B | miska C | miska D | |
|---|---|---|---|---|
| 1. ochutnanie | vydarená | pokazená | vydarená | |
| 2. ochutnanie | pokazená | vydarená | vydarená | |
| 3. ochutnanie | pokazená | pokazená | vydarená | |
| 4. ochutnanie | pokazená | vydarená | pokazená |
2. Klamal dvakrát o jednej, raz o dvoch a o poslednej neklamal
Pri polievke, o ktorej neklamal, budeme mať tri rovnaké tvrdenia a teda ju vieme určiť. Teraz potrebujeme zistiť, pri ktorej miske budú 2 rovnaké tvrdenia klamstvá. Pozrime sa na misku C. Pri tej nám aj pri prvom, aj pri treťom ochutnaní dal rovnakú informáciu. Takže buď 2-krát klamal, alebo 2-krát hovoril pravdu. 2-krát klamať však nemohol, lebo pri prvom a treťom ochutnaní misky A sme dostali rozličné tvrdenie. Takže pri prvom alebo treťom ochutnaní klamal o miske A a teda nemohol klamať o miske C.
O miske C potom musel klamať pri štvrtom ochutnaní a vďaka tomu vidíme, že o B pri štvrtom ochutnaní neklamal, B bude pokazená.
Už si ľahko všimneme, že o miske B klamal v prvom kole, lebo tam o nej tvrdil, že je vydarená a zistíme aká bola miska A.
(Červenou sú označené klamlivé tvrdenia.)
| miska A | miska B | miska C | miska D | |
|---|---|---|---|---|
| 1. ochutnanie | pokazená | vydarená | vydarená | |
| 2. ochutnanie | vydarená | pokazená | vydarená | |
| 3. ochutnanie | vydarená | vydarená | vydarená | |
| 4. ochutnanie | pokazená | pokazená | vydarená |
3. Klamal dvakrát o dvoch miskách a o ostatných neklamal
Pri dvoch miskách, o ktorých povedal 3-krát rovnaké tvrdenie, vieme, že sú všetky pravdivé. Nemôže sa stať, že by o jednej z nich hovoril vždy klamstvo, pretože o dvoch povedal dvakrát rovnaké tvrdenie a raz iné a teda by sme mali minimálne 5 klamstiev. Pri dvoch miskách, pri ktorých budeme mať 2 rovnaké tvrdenia a 1 iné, vieme, že nepravdivé tvrdenia musia byť práve tie, ktoré sú 2 rovnaké, aby nám platil počet klamstiev.
(Červenou sú označené klamlivé tvrdenia.)
| miska A | miska B | miska C | miska D | |
|---|---|---|---|---|
| 1. ochutnanie | pokazená | vydarená | vydarená | |
| 2. ochutnanie | vydarená | pokazená | vydarená | |
| 3. ochutnanie | vydarená | vydarená | vydarená | |
| 4. ochutnanie | vydarená | vydarená | vydarená |
4. Klamal trikrát o jednej miske, raz o ďalšej a o ostatných neklamal
Vidíme, že máme pri troch miskách 3 rovnaké tvrdenia a pri jednej miske máme 2 rovnaké a jedno iné tvrdenie. Jediným spôsobom ako vieme dostať 4 klamstvá je, že bude klamať pri tvrdení, ktoré je iné oproti ostatným. Potom vieme, že pri ostatných miskách, ktoré vtedy ochutnal musel hovoriť pravdu. V našom prípade teda musel klamať o miske B v 4. ochutnaní a vďaka tomu vieme, že o miskách C a D hovoril pravdu. Mohol jedine klamať o miske A.
(Červenou sú označené klamlivé tvrdenia.)
| miska A | miska B | miska C | miska D | |
|---|---|---|---|---|
| 1. ochutnanie | vydarená | pokazená | vydarená | |
| 2. ochutnanie | vydarená | pokazená | vydarená | |
| 3. ochutnanie | vydarená | vydarená | vydarená | |
| 4. ochutnanie | vydarená | vydarená | vydarená |
6. príklad
Zadanie
Vzorové riešenie
Označme si klamára K, pravdovravného P a driemajúceho boha D.
Pozrime sa najskôr na prípad, že pri stole sedí aspoň jeden klamár. Napravo od neho nemôže sedieť K, lebo by o ňom tento klamár naľavo zaklamal, že je P alebo D, čo sa podľa zadania nestalo. Môžu byť od neho napravo jedine P a D. V oboch prípadoch sa môže stať, že K o nich povie, že sú klamári.
Vieme, že P hovorí vždy pravdu. Ak je napravo od K boh D, tak tento D bude hovoriť opačne ako K, teda bude hovoriť pravdu. Teda či už napravo od K je boh P alebo boh D, tento boh hovorí pravdu, keď tvrdí, že má napravo klamára. Preto ďalší boh napravo bude znova K. Pre tohto klamára môžeme úvahu zopakovať, napravo od neho bude P alebo D, napravo od tohto K.
Toto vieme opakovať, až kým sa nedostaneme okolo stola späť ku prvému klamárovi. Celý stôl tak vyzerá nejako takto:
K,\, P/D,\, K,\, P/D,\, K,\,... ,\, P/D,\, K,\, P/D
Ako vidíme, K je každý druhý. Dokázali sme tak, že ak je K aspoň jeden, je ich práve polovica z celkového počtu, čo je 100:2=50.
Ostáva nám jedine prípad, keď nie je pri stole ani jeden K. Napravo od P ale musí byť K, preto by pri stole nemôžu sedieť ani žiadni pravdovravní. Zostalo nám teda okolo stola posadiť 100 D bohov. Každý z nich má tak po svojej ľavici D, takže všetci spanikária a mohlo sa stať, že všetci zaklamali a povedali, že boh od nich napravo je klamár.
Odpoveď: Klamárov môže byť iba 0 alebo 50.
Komentár
Častou chybou v riešeniach bolo nesprávne pochopenie toho, ako funguje driemajúci boh. Potom niektoré časti dôkazu nefungovali pre správne zadanie, čo sa odzrkadlilo aj na bodoch. Chybám tohto typu sa dá vyvarovať dôkladným čítaním zadania. Ak vám niečo nie je jasné, môžete napísať do komentárov pod zadaním, vedúci vám odpovie.
7. príklad
Zadanie
Vzorové riešenie
Všetky šálky si zafarbíme najskôr rovnakou farbou. Povedzme si, že bude zelená. Ak máme 1 šálku, tak teda budeme potrebovať 1 farbu.
Ak máme 2 a viac šálok tak vieme, že musia byť použité aspoň 2 rôzne farby, lebo ak by mali všetky rovnakú farbu nevedeli by sme ich rozoznať. Povedzme si, že bude modrá. Čiže ak máme 2 šálky potrebujeme 2 farby.
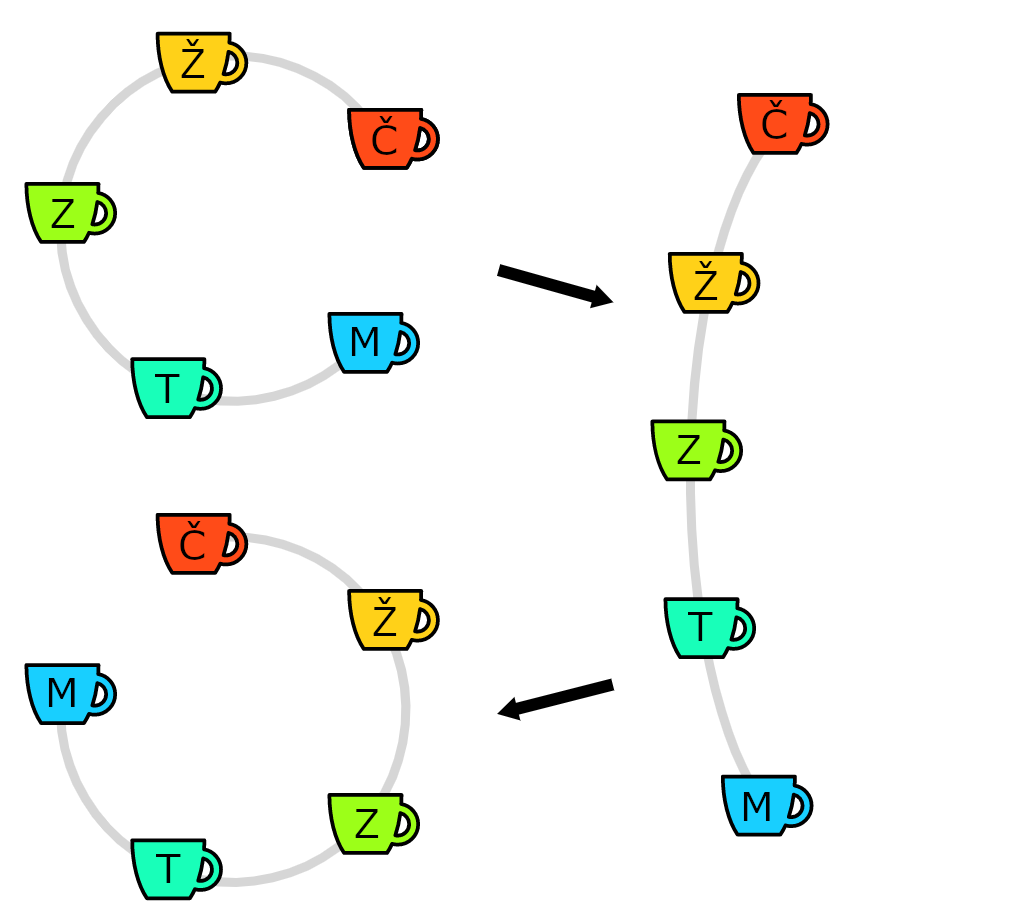
Zafarbili sme si teda jednu šálku na modro. Táto šálka nám hovorí, či boli šálky pootočené. To vieme určiť tak, že sa pozrieme o koľko bola modrá šálka posunutá čiže si vieme povedať, kde bola ktorá šálka.
To by však platilo iba kebyže Kuchár šálky pootáča, on ich však môže aj obrátiť. Na to aby sme vedeli rozoznať, či boli šálky obrátené potrebujeme si nejako označiť smer kruhu. Ako prvé nás napadne zafarbiť suseda modrej šálky na inú farbu, povedzme, že na červenú a dáme ju napravo od modrej. Ak by prišlo k obráteniu šálok, táto červená šálka by susedila s modrou z “opačnej strany” - bola by naľavo od modrej šálky. Čiže pre n≥3 budeme teoreticky potrebovať najviac 3 farby.
Myšlienka s obracaním však ide trochu vylepšiť. Namiesto červenej šálky vieme použiť 2 modré. To by fungovalo tak, že si napravo vedľa modrej necháme zelenú šálku a za ňou budeme mať 2 modré šálky vedľa seba. Tak vieme povedať, či bol zmenený smer, lebo ak by prišlo k obráteniu šálok, tieto dve modré šálky by boli naľavo od tejto jednej modrej šálky. Na to aby sme to vedeli povedať jednoznačne musí byť z druhej strany medzi modrou a 2 modrými šálkami aspoň 2 zelené. Ak by ich bolo 0 tak by sme mali v podstate 3 modré šálky vedľa seba, čiže by sme nevedeli povedať či boli šálky obrátené a kebyže je 1 tak tiež, lebo dvojica modrých šálok je rovnako ďaleko zprava aj zľava čiže tiež nevieme určiť či boli šálky obrátené. Preto toto vylepšenie platí len pre n \geq 6.
Odpoveď: Ak n=1 tak potrebujeme 1 farbu, ak n=2 tak 2, ak n=3;4;5 potrebujeme 3 farby a pre n \geq 6 potrebujeme 2 farby.
8. príklad
Zadanie
Vzorové riešenie
Označme si priesečník priamok AD a BC ako X. Uhol, ktorý nás zaujíma je teda \measuredangle AXB. Ľahko si všimneme, že uhol \measuredangle ACX susedí so zadaným uhlom \measuredangle ACB. Jeho veľkosť tak bude 180 \degree - 74 \degree = 106 \degree. Stačí nám teraz už len dorátať zvyšný uhol trojuholníka ACX (\measuredangle CAX) a budeme vedieť dopočítať ten, ktorý hľadáme.
Posledné, čo sme zo zadania nepoužili je bod P'. Vieme, že vznikol osovou súmernosťou bodu P podľa priamky AD. Platí preto, že uhly \measuredangle DAP' a \measuredangle DAP sú rovnako veľké. Vieme tiež, že priamka AP' je rovnobežná s priamkou BC. To už nám dáva všetko, čo potrebujeme. Uhly \measuredangle ACB a \measuredangle P'AC sú striedavé, takže majú rovnakú veľkosť. Uhol \measuredangle CAX je polovicou uhla \measuredangle P'AC, takže jeho veľkosť je 74 \degree : 2 = 37 \degree. Takže |\measuredangle AXC| = 180 \degree - 106 \degree - 37 \degree = 37 \degree.
Odpoveď: Priamky AD a BC zvierajú uhol 37 \degree.
9. príklad
Zadanie
Vzorové riešenie
Ak na začiatku skúšame nájsť nejaké vyhovujúce kombinácie kartičiek, zišiel by sa nám nejaký postup, pomocou ktorého jednoducho zistíme, či je dané číslo deliteľné jedenástimi. Jedno, asi najjednoduchšie, a v tomto prípade určite najpraktickejšie pravidlo znie takto:
Číslo je deliteľné jedenástimi práve vtedy, keď je deliteľný jedenástimi rozdiel súčtu cifier na párnych pozíciách P a súčtu cifier na nepárnych pozíciách N. Teda napríklad, pre číslo 9341111144111111112 platí:
N=9+4+1+1+4+1+1+1+1+2=25
P=3+1+1+4+1+1+1+1+1=14
Rozdiel týchto súčtov je N-P=25-14=11, čo je násobok 11. Z toho vyplýva že aj toto 19-ciferné číslo je násobok 11. Toľko k deliteľnosti, teraz toto pravidlo skúsime využiť v náš prospech.
Ľahko vieme ukázať, že kartičky použité na takéto číslo nebudú (až na špeciálne prípady) spĺňať druhú podmienku zo zadania. Keď totiž vymeníme napríklad prvú a tretiu cifru, dostaneme nové číslo, no súčty P a N sa nezmenia, iba sa v druhom z nich zmení poradie ščítancov. To nevadí, keďže ščítavanie je komutatívne, a teda pri ňom nezáleží práve na poradí sčítancov. Môžeme teda v oboch súčtoch, párnych aj nepárnych cifer, tieto cifry ľubovoľne povymieňať.
Aby sme splnili zadanie, číslo sa ani po žiadnej výmene cifier nemôže zmeniť. Inak povedané, všetky cifry ktoré vieme vymeniť musia byť rovnaké. Jediné čísla, ktoré teda môžu teoreticky spĺňať zadanie sa skladajú iba z dvoch striedajúcich sa cifier : 10 cifier A na nepárnych pozíciách a 9 cifier B na párnych. Ich súčty teda budú N=10\cdot A a P=9\cdot B, kde pre A aj B máme možnosti od 1 po 9. To nie je až tak veľa, preto si môžeme spraviť tabuľku, kde v prvom riadku budú všetky možné hodnoty N=10\cdot A, v prvom stĺpci možnosti pre P=9\cdot B, a v každom vnútornom políčku tabuľky bude ich rozdiel:
| Možné súčty |
10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
|---|---|---|---|---|---|---|---|---|---|
| 9 | 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 |
| 18 | -8 | 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 |
| 27 | -17 | -7 | 3 | 13 | 23 | 33 | 43 | 53 | 63 |
| 36 | -26 | -16 | -6 | 4 | 14 | 24 | 34 | 44 | 54 |
| 45 | -35 | -25 | -15 | -5 | 5 | 15 | 25 | 35 | 45 |
| 54 | -44 | -34 | -24 | -14 | -4 | 6 | 16 | 26 | 36 |
| 63 | -53 | -43 | -33 | -23 | -13 | -3 | 7 | 17 | 27 |
| 72 | -62 | -52 | -42 | -32 | -22 | -12 | -2 | 8 | 18 |
| 81 | -71 | -61 | -51 | -41 | -31 | -21 | -11 | -1 | 9 |
Zvýraznené sú násobky 11, ktoré môžu byť aj záporné. Samozrejme dá sa to povedať aj matematickejšie než tabuľkou.
Nech N-P=10\cdot A-9\cdot B=11\cdot A-A-11\cdot B+2\cdot B je deliteľný jedenástimi. Z toho vyplýva, že 2\cdot B-A musí byť tiež deliteľné 11. Keďže A aj B sú kladné celé jednociferné čísla rozdiel 2\cdot B-A môže nadobúdať iba hodnoty od -7 po 17. Z nich sú deliteľné jedenástimi iba 0 a 11. Teda buď 2\cdot B-A=0 alebo 2\cdot B-A=11. To nám dá rovnaké riešenia ako máme zvýraznené v tabuľke. Sú to:
| Číslo | 10 kartičiek (A) | 9 kartičiek (B) |
|---|---|---|
| 1616161616161616161 | 1 | 6 |
| 2121212121212121212 | 2 | 1 |
| 3737373737373737373 | 3 | 7 |
| 4242424242424242424 | 4 | 2 |
| 5858585858585858585 | 15 | 8 |
| 6363636363636363636 | 6 | 3 |
| 7979797979797979797 | 7 | 9 |
| 8484848484848484848 | 8 | 4 |
Tieto riešenia spĺňajú nami vytvorené kritéria, ktorými sme si možnosti zúžili. To ale ešte nijak nezaručuje, že sa cifry nebudú dať preusporiadať aj inak ako len na miestach rovnakej parity, tak že sa deliteľnosť 11 zachová. Opäť vďaka komutativite sčítavania je jedno, ktoré párne číslo s ktorým nepárnym vymeníme, a teda by stačilo si napríklad vytvoriť podobnú tabuľku ako vyššie pre každé získané riešenie, a počet výmen od 1 po 9. No s trochou znalostí to pôjde aj jednoduchšie. Keď totiž vymeníme dve cifry medzi našimi súčtami, rozdiel týchto dvoch súčtov sa zmení o najviac 8 (v prípade že A=9 a B=1 alebo naopak), a takúto výmenu vieme urobiť 9-krát. Dokopy sa teda rozdiel zmení o súčin dvoch jednociferných čísel, z čoho nikdy nevznikne násobok 11, pretože 11 je prvočíslo, teda neviem vzniknúť násobením menších čísel.
Tým sme teda ukázali, že po poprehadzovaní kartičiek sa rozdiel v pravidle deliteľnosti zmení o číslo ktoré nie je násobkom 11, a teda výsledné číslo nebude deliteľné jedenástimi. Preto budú riešeniami práve všetky nami nájdené kombinácie kartičiek (viď druhá tabuľka).
10. príklad
Zadanie
Vzorové riešenie
Označme D priesečník kolmice BH a strany trojuholníka AC.
Keďže AH je os uhla \measuredangle CAB tak |\measuredangle HAB|=|\measuredangle HAD|. Taktiež priamka HB je kolmá na os AHa preto |\measuredangle AHB| = |\measuredangle AHD| = 90^\circ. Potom si môžeme všimnúť, že \triangle DHA je zhodný s \triangle BHA podľa vety usu. Majú totižto spoločnú stranu AH a uhly prislúchajúce tejto srane majú rovnakú veľkosť. Z toho vyplýva dĺžka strán |AD|=|AB|=4 a že bod H je stredom úsečky BD keďže |HB|=|HD|.
Všimnime si, že MH je stredná priečka \triangle DBC, keďže M je stred strany BC a H je stred strany BD. Ako je všeobecne známe dĺžka strednej priečky je polovica dĺžky rovnobežnej strany daného trojuholníka. Takže v našom prípade |MH|=\frac{|DC|}{2}. Teda ak by sme vypočítali dĺžku úsečky DC, tak to už máme takmer doriešené. Keďže bod D leží na úsečke AC, tak dĺžku úsečky DC vieme vypočítať ako |AC|-|AD|=6~\text{cm}-4~\text{cm}=2~\text{cm} a teda |MH|=\frac{|DC|}{2}=\frac{2\text{cm}}{2}=1~\text{cm}.
Odpoveď: Dĺžka úsečky MH je 1~\text{cm}.
Prémia 1
Zadanie
- Každá linka je cyklus, teda začína na rovnakej zastávke ako končí
- Linka neprechádza viac krát jednou zastávkou
- Každá linka má najmenej 10 zastávok
- Po každej ulici musí prechádzať aspoň jedna linka

Vzorové riešenie
Riešenie
Najmenší súčet dĺžok liniek, ktorý sa vám podarilo dosiahnuť bol 96. Na obrázku je jedno z takýchto riešení. (Každá farba predstavuje jednu linku.)

Bodovanie:
- Súčet 96 - 6 bodov.
- Súčet 97 až 103 - 5 bodov.
- Súčet 104 až 108 - 4 body.
- Súčet 109 až 114 - 3 body.
- Súčet 115 až 119 - 2 body.
- Súčet 120 a viac - 1 bod.

