Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×1. príklad
Zadanie
Vzorové riešenie
Ako prvé si musíme uvedomiť ako chce dračica potápať lode, aby čo najdlhšie vydržala. To je jednoduché - vždy chce potopiť jednu z lodí, ktoré sú k nej najbližšie, lebo tie sa najskôr dostanú na ostrov.
Keďže vieme, že lode sa každé ráno posunú o 1 míľu a večer je 1 loď zostrelená, tak si vieme predstaviť ako to bude vyzerať (zobrazené sú stavy na konci dňa, preškrtnutá loď je večer potopená dračicou):
| 1. míľa | 2. míľa | 3. míľa | |
|---|---|---|---|
| 1. deň |  |
||
 |
|||
 |
|||
| 2. deň |  |
 |
|
 |
 |
||
 |
|||
| 3. deň |  |
 |
 |
 |
 |
||
 |
 |
Z tejto tabuľky vidíme, že každý 3. deň je zničený rad lodí (lode ktoré boli vyslané v ten istý deň) a teda vtedy sa vzdialenosť od ostrova nezmení. Keďže sa toto bude každé 3 dni opakovať, tak vieme si z toho vyjadriť za aký čas prejdeme 1 míľu: \frac{3}{2} (za 3 dni prejdeme 2 míle).
Teraz keď vieme ako dlho trvá prejsť 1 míľu, tak vieme z toho vypočítať koľko to má trvať pre 142 míľ: 142\cdot\frac{3}{2}=213. Vypočítali sme, že to bude trvať 213 dní, ale tu si treba dať pozor! Z tabuľky vidno aj fakt, že 2 míle prejdeme aj za 2 dni (treba si spomenúť, že každý 3. deň sa vziadelnosť medzi loďami a ostrovom nemení). My sme vypočítali iba za koľko prejdú celé rady lodí.
Logickou úvahou teraz vieme prísť na to, že v poslednom dni nášho posledného 3-dňového cyklu (kedy sa ponorí celý rad lodí) sa tiež nezmenila vzdialenosť oproti predposlednému dňu a teda tento nadbytočný deň môžeme odstrániť: 213 - 1 = 212.
Taktiež si to môžeme skúsiť aj vypočítať - koľko krát sa zopakovalo ponorenie celého radu lodí: 213\div3=71 (213 dní trvalo kým sa celé rady lodí dostali na ostrov a 3 dni trvá, kým sa jeden celý rad lodí potopí).
Teraz si zistíme koľko míľ prejdeme za 70 opakovaní: 70\cdot2=140 a čas koľko to trvalo: 70\cdot3=210. A teda na 211. deň to bude vyzeraž ako v 1. deň - na 141. míľu sa ráno dostanú 3 lode, večer dračica 70 potopí a ostanú 2. Následne 212. deň sa ráno dostanú 2 lode na 142. míľu... Teraz sme vlastne skončili, lebo sa lode práve dostali na ostrov.
Odpoveď: Dračica dokáže vzdorovať maximálne 212 dní.
Komentár
Veľa z Vás zabudlo na konci riešenia na to, že 2 míle prejdeme aj za 2 dni a na tom ste zbytočne stratili body.
2. príklad
Zadanie
V kráľovskom paláci bolo vedľa seba 2022 komnát na jednej chodbe. Každá komnata mala vlastné dvere, na ktorých bolo vygravírované číslo. Každé štyri po sebe idúce dvere mali súčet svojich čísel 25. Palác bol ale starý a o nič mladšie neboli ani dvere, takže sa niektoré čísla komnát časom ošúchali, a iba na troch najmenej používaných komnatách sú doteraz viditeľné. Na obrázku vidíme prvé štyri a posledné štyri dvere. Aké číslo mali dvere komnaty princa Mimriška, ktorá bola úplne na konci chodby?

Vzorové riešenie
Ako prvé sa môžeme pozrieť na hociktorých 5 po sebe idúcich dverí. Označme si čísla na nich postupne ako a, b, c, d, e. Potom platia nasledovné dva súčty:
a+b+c+d=25,
b+c+d+e=25.
Teraz si môžeme všimnúť že pravé strany sú v oboch rovniciach 25 takže sa nám rovnajú aj ľavé strany
a+b+c+d=b+c+d+e.
Vidíme že na oboch stranách je b+c+d takže to môžeme odčítať z oboch strán a dostaneme a=e. To znamená že ak majú n-té dvere v poradí číslo a tak aj dvere na (n+4)-tom mieste budú mať číslo a.
Teraz sa teda pozrieme na čísla, ktoré poznáme. Vieme že na 1. mieste je číslo 6. Takže na mieste 1+4 bude tiež 6 aj na 1+4+4 bude 6. Toto vieme opakovať stále takže všeobecne vieme povedať že na každom mieste ktoré je o 1 väčšie ako násobok 4 bude číslo 6. Na 3. mieste je číslo 7, to znamená že na každom mieste ktoré je o 3 väčšie ako násobok 4 bude číslo 7.
Pozrime sa teda na posledné 4 čísla. Posledné číslo je na 2022. pozícii to znamená že je o 2 väčšie ako násobok 4. Číslo pred ním teda bude 6 lebo to je na pozícii o 1 väčšeej ako násobok 1. 2019. dvere (4. od konca) majú číslo 7 lebo sú na mieste o 3 väčšom ako násobok 4.
Posledné 4 dvere sú teda v poradí 7, 9, 6, ?. Teraz nám stačí vyrátať otáznik. Vieme že súčet každých 4 po sebe idúcich čísel je 25 takže 7+9+6+{?}=25. To znamená že otáznik má hodnotu 3.
Odpoveď: Dvere komnaty princa Mimriška majú číslo 3.
3. príklad
Zadanie
 Mimriškovo okno malo tvar obdĺžnika ktorý sa skladá z menších sklenených tabúľ, ako je nakreslené na obrázku. Všetky tieto tabule majú tvar štvorca, a najmenšia z nich (biela) chýba. Aký je obsah celého okna, ak vieme že chýbajúca tabuľa má strany dĺžky 1 \, \text{dm}?
Mimriškovo okno malo tvar obdĺžnika ktorý sa skladá z menších sklenených tabúľ, ako je nakreslené na obrázku. Všetky tieto tabule majú tvar štvorca, a najmenšia z nich (biela) chýba. Aký je obsah celého okna, ak vieme že chýbajúca tabuľa má strany dĺžky 1 \, \text{dm}?
Vzorové riešenie
Ako prvé si na obrázku vyznačme dĺžky jednotlivých strán štvorcov. Písmená sú pridelené podľa prvých písmen anglických farieb, aby sme sa vyhli nepríjemnostiam so z-ž.

Poďme si teraz vyjadriť všetky dĺžky pomocou strán bieleho a oranžového štvorca. Z obrázka je potom vidno, že g=2 \cdot o a tiež p=2 \cdot o + 1~\text{dm}, keďže majú spoločnú hranu. Z tohto potom vieme aj y= p + 1~\text{dm} =2 \cdot o + 2~\text{dm}. Nakoniec musí platiť aj 2 \cdot b= y + 1~\text{dm} =2 \cdot o + 3~\text{dm}, z čoho b=o + 1{,}5~\text{dm}.
Vieme však, že celé okno je obdĺžnik, a teda jeho ľavá a pravá hrana sa rovnajú. V našom vyjadrení:
p+o+g=y+b.
Po dosadení dostávame
2 \cdot o+ 1~\text{dm}+o+2 \cdot o=2 \cdot o + 2~\text{dm}+o + 1{,}5~\text{dm}, \\ 5 \cdot o + 1~\text{dm}=3 \cdot o + 3{,}5~\text{dm}, \\ 2 \cdot o=2{,}5~\text{dm}, \\ o=1{,}25~\text{dm}.
Vieme si teda, podľa predošlých vyjadrení, dopočítať, že p=3{,}5~\text{dm}, y=4{,}5~\text{dm}, b=2{,}75~\text{dm}. Teraz už máme dosť informácii a vieme vypočítať obsah celého okna:
S_{okno}=(p+y) \cdot (y+b)= 8~\text{dm} \cdot 7{,}25~\text{dm} = 58~\text{dm}^2.
Odpoveď: Obsah celého okna je 58~\text{dm}^2.
Komentár
Príklad ste väčšinou zvládli. Niektorí z vás by si mali dávať pozor na hlúpe chyby, za ktoré ste podľa veľkosti chyby stratili pár bodov.
4. príklad
Zadanie
Vzorové riešenie
Mimo nádvoria je 30 ľudí. Mimo hradieb je iba 26 ľudí, čiže na hradbách ich musí byť o 4 viac ako na nádvorí (keďže spolu je ich stále rovnako veľa). Podobne v kuchyni musí byť o 9 viac ľudí ako na nádvorí a v posteli o 15. Označme si teda počet ľudí na nádvorí N. Z toho si vieme vyjadriť aj všetky ostatné počty okrem počtu v komnatách. O ňom zatiaľ nevieme nič, takže si ho označme ako K.
Vieme, že napríklad mimo nádvoria je 30 ľudí, ale to je zároveň súčet ľudí na všetkých ostatných miestach. Platí teda:
\displaystyle N + 4 + N + 9 + N + 15 + K = 30 \\ 3N + 28 + K = 30 \\ 3N + K = 2
Ak by N bolo viac ako 0, tak by pravá strana bola príliš veľká, zostáva nám teda len jediná možnosť N = 0. Z poslednej rovnice potom vidíme, že K = 2, a ostatné počty dopočítame podľa prvého odseku.
Odpoveď: Na nádvorí nebol nikto, na hradbách 4 ľudia, v kuchyni 9, v posteli 15 a v komnatách 2.
Iné riešenie
Zišlo by sa nám vedieť, koľko je spolu všetkých ľudí, lebo potom by sme z toho vedeli povedať aj počty na jednotlivých miestach. Označme si teda celkový počet ľudí S. Potom vieme, že na nádvorí bolo S - 30 ľudí, na hradbách S - 26, v kuchyni S - 21 a v posteli S - 15. O počte ľudí v komnatách nám to tiež nič nehovorí, takže ten zatiaľ nechajme ako K.
Tým sme si vyjadrili počty na jednotlivých miestach. Povedali sme si, že ich súčet je S, ale ten si vieme rozpísať aj ako súčet jednotlivých miest. Musí teda platiť:
\displaystyle S - 30 + S - 26 + S - 21 + S - 15 + K = S \\ 4S - 92 + K = S \\ 3S + K = 92
Z toho vidíme, že S môže byť najviac 30, inak by ľavá strana bola príliš veľká. Zároveň ale platí, že S musí byť aspoň 30, lebo už len mimo nádvoria je 30 ľudí. Spolu teda musí byť práve 30 ľudí a z toho už ľahko dopočítame jednotlivé počty.
Odpoveď: Na nádvorí nebol nikto, na hradbách 4 ľudia, v kuchyni 9, v posteli 15 a v komnatách 2.
5. príklad
Zadanie
- V prvej fľaši na najbližší menší alebo rovný násobok 2 \, \text{ml}.
- V druhej fľaši na najbližší násobok 3 \, \text{ml}.
Vzorové riešenie
Pozrime sa najprv na to, ako vôbec môžeme preliatím získať viac vody. Zo zadania je zrejmé, že v 1. fľaši sa objem nikdy nezaokrúhli na vyššie číslo. Celkový objem vody teda musíme zväčšovať zaokrúhľovaním v 2. fľaši. V nej môže po preliatí zostať rôzny objem, nás však zaujíma iba jeho zvyšok po delení tromi. Rozoberieme teda všetky tri možnosti.
Keď prelejeme číslo deliteľné 3, tak objem v 2. fľaši sa nebude na nič zaokrúhľovať, objem v nej zostane násobkom 3.
Ak prelievame objem, ktorý má zvyšok 1 po delení tromi, teda je o 1 väčší ako násobok 3, tak pri prelievaní z 1. fľaše do 2 sa nám objem v 2. fľaši zaokrúhlením zmenší o 1. Ak však prelievame takýto objem z 2. fľaše do 1., tak sa nám objem v 2. fľaši zväčší naspäť o 1, keďže ubudlo o 1 viac ako násobok 3. Ak sa nám ešte podarí, aby bol prelievaný objem párny, nestratíme vodu zaokrúhľovaním v 1. fľaši a celkový objem sa zväčší o 1.
Ak pracujeme s objemom so zvyškom 2, teda o 1 menším ako násobok 3, tak sa po odliatí do 2. fľaše zaokrúhli nahor. Opäť ak to bude zároveň aj párne číslo, nestratíme vodu zaokrúhľovaním nadol v 1. fľaši a celkový objem sa zväčší o 1. Opačným preliatím vodu nezískame, keďže nám v 2. fľaši ostane objem, ktorý sa zaokrúhli nadol.
Vidíme teda teraz, že po jednom preliatí sa nám môže objem zväčšiť maximálne o 1, keď odlievame z 2. fľaše párne číslo o 1 väčšie ako násobok 3 (4,10,\ldots) alebo keď do nej prilievame párne číslo o 2 väčšie ako násobok 3 (2,8,\ldots).
Teraz už poďme skúsiť prelievať, a uvidíme, kam sa dostaneme. Skúsime čo najviac využívať, že vieme preliať 2 ml do 2. fľaše a získať pri tom vodu. Začíname s 30 ml vody, vždy prelievame po 2 ml, a keď sa nám voda minie, prelejeme si čo najviac naspäť:
- 10-krát prelejeme 2 ml z 1. fľaše do 2. fľaše. Vo fľašiach máme 10 ml a 30 ml.
- Prelejeme 20 ml z fľaše 2 do 1 vo fľašiach máme 30 a 9 ml.
- 7-krát prelejeme 2 ml z fľaše 1 do fľaše 2. Vo fľašiach máme 16 ml a 30 ml.
- Prelejeme 14 ml z 2. fľaše do 1. vo fľašiach máme 30 a 15 ml.
- 5-krát prelejeme 2 ml z 1. fľaše do 2. Vo fľašiach máme 20 ml a 30 ml.
- Prelejeme 10 ml z 2. fľaše do 1. Vo fľašiach máme 30 a 21 ml.
- 3-krát prelejeme 2 ml z 1. fľaše do 2. fľaše. Vo fľašiach máme 24 ml a 30 ml.
- Prelejeme 6 ml z 2. fľaše do 1. vo fľašiach máme 30 a 24 ml.
- 2-krát prelejeme 2 ml z 1. fľaše do 2. fľaše. Vo fľašiach máme 26 ml a 30 ml
- Prelejeme 4 ml z 2. fľaše do 1. Vo fľašiach máme 30 a 27 ml.
- Prelejeme 2 ml z 1. fľaše do 2. fľaše. Vo fľašiach máme 28 ml a 30 ml, spolu 58 ml.
Ani po dlhšom snažení sa nám nepodarí dosiahnuť väčší objem. Pokúsime sa teda ukázať, že sme naozaj dosiahli maximum, ako to vyžaduje zadanie. Keďže po každom preliatí vieme zväčšiť množstvo vody najviac o 1 ml vieme, že krok pred tým ako zväčšíme objem na nejaké čislo, museli sme ho tesne predtým mať o 1 menší, a niekedy pred tým ešte o 1 menší až po 30 ml. Teda ak by sme chceli dosiahnuť 60 ml, museli by sme pred tým vo fľašiach mať 59 ml. Vo fľašiach ale 59 ml nemôžeme mať, pretože jediný spôsob ako to dosiahnuť by bol, že v jednej z fľaší je 29 ml s v druhej 30. 29 ale nie je deliteľné 2 ani 3, a teda by sa v v oboch fľašiach zaokrúhlilo. Nevieme teda dosiahnuť 59 ani 60 ml, a našich dosiahnutých 58 ml je naozaj najviac.
Odpoveď: Najviac vieme dosiahnuť 58 ml vody, napríklad spôsobom ako je popísané v riešení.
Komentár
Skoro všetkým riešiteľom sa úspešne podarilo nájsť postup, akým dostaneme 58 ml elixíru, a aj ukázali, že ďalším prelievaním z tohto stavu viac elixíru nedostaneme. To, žiaľ, nie je dôkaz, že viac elixíru nedostaneme, ak budeme prelievať úplne iným spôsobom. Napríklad by bolo treba ukázať, prečo nevieme dostať 59 alebo 60 ml jedným preliatím z iného stavu, napríklad s iným objemom elixíru.
6. príklad
Zadanie
- Zistite, kde sa nachádzali po 27 presunoch.
- Zistite z akých deviatich presunov sa skladala ich pôvodná trasa.

Vzorové riešenie
Šošo a jeho čata prešli za celý čas svoju trasu trikrát, a potom ešte prvé tri presuny zo štvrtého opakovania, kým sa dostali do bodu D (15+7+8=3 \cdot 9+3). Po troch prejdeniach trasy, čiže 27 presunoch sa nachádzajú na trikrát väčších súradniciach ako po jej prvom prejdení, keďže prejdením trasy sa vždy posunuli rovnako, a začínali na [0;0]. Teda obe súradnice, vodorovná aj zvislá, vtedy budú deliteľné 3. Keďže o 3 presuny neskôr už boli v D, zaujímajú nás iba tie z nich, ktoré sú od D vzdialené maximálne 3. Týmto dostávame len 5 možností kde sa mohli po 27 presunoch nachádzať, no priamo v D to byť nemohlo, pretože nevieme spraviť 3 presuny tak, aby sme sa vrátili do D (musí ich byť párny počet, za každý presun nejakým smerom sa potom musíme vrátiť opačným). Na obrázku sú zaznačené modrou:
Z každej z týchto pozícií je len jedna cesta ako sa na tri presuny vieme dostať do bodu D, a to rovno, 3 presuny priamo do smeru ktorým je D. To nám už určí prvé tri z deviatich presunov na trase. Skúsme si preto pre každú možnosť rozobrať, čo nám to o zvyšku trasy hovorí, a ktoré trasy by mohli sedieť.
Ak sú po 27 ťahoch v E=[6;9] alebo F=[9;6].V oboch prípadoch sa zameriame na pohyb tým smerom, v ktorom sa musíme dostať až na súradnicu 9. Ukážeme si argument pre prípad s E, a rovnako vieme argumentovať aj v prípade s F. Vieme, že z bodu E, kde začíname nové opakovanie trasy, idú tri kroky do D, teda prvé tri presuny trasy sú smerom dole. Táto trasa sa pred príchodom do E zopakovala trikrát, vždy začínajúc troma presunmi dole, teda dokopy sa pohnú dole aspoň 9-krát. E však leží od bodu A 9 posunov opačným smerom, preto by zo zvyšných 18 pohybov v prvých troch cykloch všetky museli smerovať hore, aby mali šancu skončiť aspoň na výške bodu E. Potom by však neostali už žiadne presuny na to, aby sme sa dostali o 6 miest doprava, kde E leží, lebo všetkých 27 presunov robíme iba vertikálne.
Podobne pri bode F, aby sme sa vzhľadom na nutných 9 presunov doľava vedeli dostať dostatočne doprava, museli by všetky ostatné presuny smerovať tam, a nemali by sme sa ako dostať o 6 presunov hore.
Ak sú po 27 ťahoch v G=[6;3].Vieme, že na to, aby sa dostali z G do D, musia byť prvé 3 posuny trasy hore. Okrem toho, ak sa po 3 trasách nachádzajú na súradniciach [6; 3], tak každá trasa ich posunula o tretinu z celkovej zmeny, teda celkovo o 2 presuny doprava a o 1 hore. Vieme teda, že po 21 presunoch, teda dvoch prejdeniach trasy a troch krokoch sa budú nachádzať na [2 \cdot 2, 2 \cdot 1] a ešte o prvé tri kroky vyššie, teda na [4;5]. Bod C sa však nachádza na [5;3], a musia sa tam dostať už po 15+7=22 presunoch, čo je hneď po najbližšom, aj keď spolu tieto body nesusedia. V tomto prípade teda tiež nevieme splniť podmienku zo zadania.
Podobne ako v predošlom prípade, aj tu vieme zistiť, že prvé tri presuny trasy smerujú doprava, a každá trasa ich musela dokopy posunúť o [+1; +2]. Ďalej sa pozrieme, ako sa mohli dostať do bodu C. Pozíciu po 18 presunoch poznáme, je to [2 \cdot 1; 2 \cdot 2]=[2;4], a potom znova opakujú trasu od začiatku, teda začínajú tromi presunmi doprava na [5; 4]. Hneď v nasledujúcom ťahu musia byť na C=[5; 3], teda sa v štvrtom presune trasy pohnú dole.
So znalosťou prvých štyroch presunov trasy sa pozrieme čo sa stane po jej prvom prejdení. Dostávame sa z [1,2] tromi presunmi doprava a jedným dole na [4;1]. To je zatiaľ 13 presunov z pätnástich, po ktorých majú byť v B. Za zvyšné dva presuny sa na [3; 2] vedia dostať len kombináciou presunu doľava a hore, no nemôžu sa vrátiť hore po ceste ktorou prišli, a preto začnú presunom doľava. Teraz im už chýba prejsť iba posledné tri presuny, aby dokončili druhé opakovanie trasy, ktorého konečný bod vieme vypočítať ako 2*[1;2]=[2;4]. Pôjdu tam teda dvoma presunmi hore a jedným doľava. Ten presun vľavo nemôžu spraviť hneď, lebo tadiaľ už raz išli, a ani ako posledný, lebo hneď na začiatku ďalšej trasy pôjdu doprava, čo by bolo po rovnakom úseku. Teda tam pôjdu v poradí hore, doľava hore.
Odpoveď: Výsledná trasa po ktorej išli je teda doprava, doprava, doprava, dole, doľava, hore, hore, doľava, hore.
Komentár
V tomto príklade sa mohlo zdať náročné vôbec začať, hlavne bez uvedomenia že súradnice po presune 27 musia byť násobkom troch. Viacerí z vás to však zvládli aj bez toho, okrem postupu spomenutého v tomto vzorovom riešení sa dalo ku príkladu postupovať aj na základe iných obmedzujúcich informácií alebo pomocou rovníc. Celkovo však treba povedať, že riešitelia ktorí sa príklad odhodlali odovzdať ho poväčšinou úspešne vyriešili bez väčších problémov.
7. príklad
Zadanie
Vzorové riešenie
Rovnicu ekvivalentne upravujeme. Obe strany vynásobíme mn a následne vyjmeme na ľavej strane m a na pravej n.
m+\dfrac{1}{n}=n+\dfrac{1}{m}
m^2n+m=n^2m+n
m(mn+1)=n(mn+1)
Všetko si dáme na jednu stranu a nasledovne upravíme:
m(mn+1)-n(mn+1)=0
(m-n)(mn+1)=0
Vieme že súčin dvoch zátvoriek je rovný 0 ak aspoň jedna zo zátvoriek má hodnotu 0. Čiže v našom prípade buď (m-n)=0 alebo (mn+1)=0. Zároveň potom platí aj naša pôvodná rovnica.
Pokiaľ (m-n)=0 tak potom m=n. Ak sa však (m-n)\neq0, tak potom druhá zátvorka (mn+1) musí byť rovná 0. Potom mn=-1. Uvedomme si, že -1 vieme dostať súčinom dvoch celých čísel len ako súčin -1 a 1. Čiže v našom prípade [m,n] musí byť [-1,1] alebo [1,-1].
Odpoveď: Všetky celočíselné riešenia [m,n] rovnice zo zadania sú [-1,1], [1,-1] a [m,m] (teda m = n).
8. príklad
Zadanie
Vzorové riešenie
V 12. ťahu by sa Turbanovci museli pohnúť 2048 políčok. Keďže na šachovnici nie sú žiadne dve políčka vzdialené 2048, zaručene prehrajú.
Naopak, až do 10. ťahu sa každý určite bude vedieť pohnúť. V týchto ťahoch sa hýbu najviac o 512. Ak by sa nevedeli pohnúť ani doľava ani doprava, znamenalo by to, že naľavo aj napravo od nich je najviac 511 políčok (to isté platí o smeroch hore, dole). To by znamenalo, že tabuľka má na šírku (a výšku) najviac 511+1+511=1023 políčok, čo nie je pravda. Všeobecne platí, že sa určite vieme pohnúť o x vo štvorci so stranou aspoň 2x. Toto využijeme aj neskôr v riešení.
Rozhodujúce teda je len to, či sa stráži podarí v 11. ťahu pohnúť. Na to aby sa mohla pohnúť doprava, musí mať napravo od seba aspoň 1024 políčok, teda musí byť v stĺpcoch 1 až 997 (2021-1024=997). Aby sa mohla pohnúť doľava musí mať naľavo od seba aspoň 1024 políčok, teda musí byť v stĺpcoch 1025 až 2021. Zostávajú teda stĺpce 998 až 1024, z ktorých sa nedá pohnúť ani doľava ani doprava. Tak isto riadky, z ktorých sa nedá pohnúť anu hore ani dole, sú 998 až 1024. To nám vytvára jeden štvorec 27\times 27 v strede šachovnice (červený štvorec).
Aby Turbanovci vyhrali, museli by sa v 10. ťahu pohnúť do tohto štvorca. Tam sa dokážu dostať zo štyroch štvorcoch, jeden v každom smere, posunutých o 512 políčok oproti červenému štvorcu (oranžové štvorce).
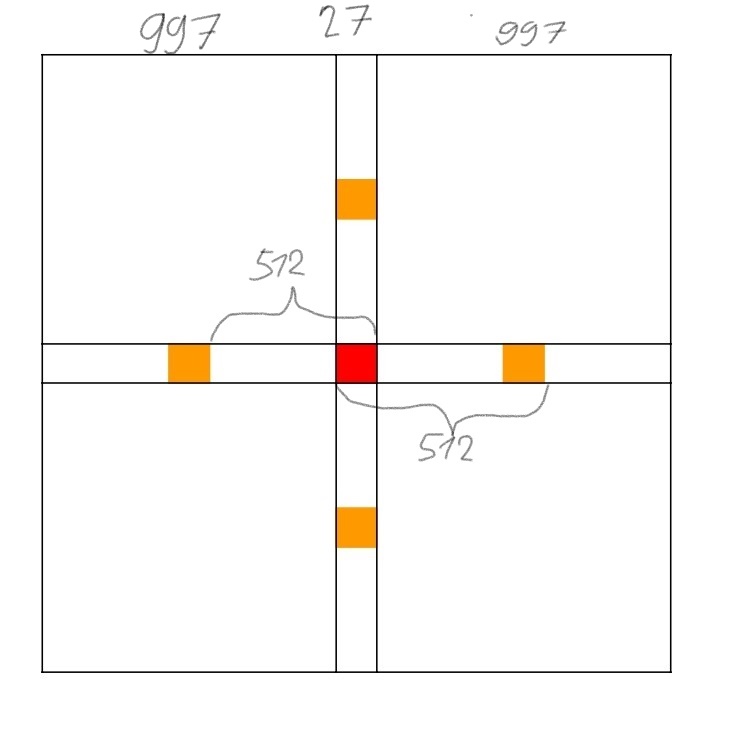
Ukážeme, že stráž dokáže zabrániť tomu aby sa Turbanovci nachádzali na začiatku 10. ťahu v ľubovoľnom z týchto štvorcov.
Ak sa stráž na začiatku 9. ťahu nachádza v zelenom štvorci v strede, pohne sa tak, aby v ňom zostala. Strana tohto štvorca je 512+512-27=997, teda určite sa tak bude vedieť pohnúť lebo 997\geq 2\cdot 256.
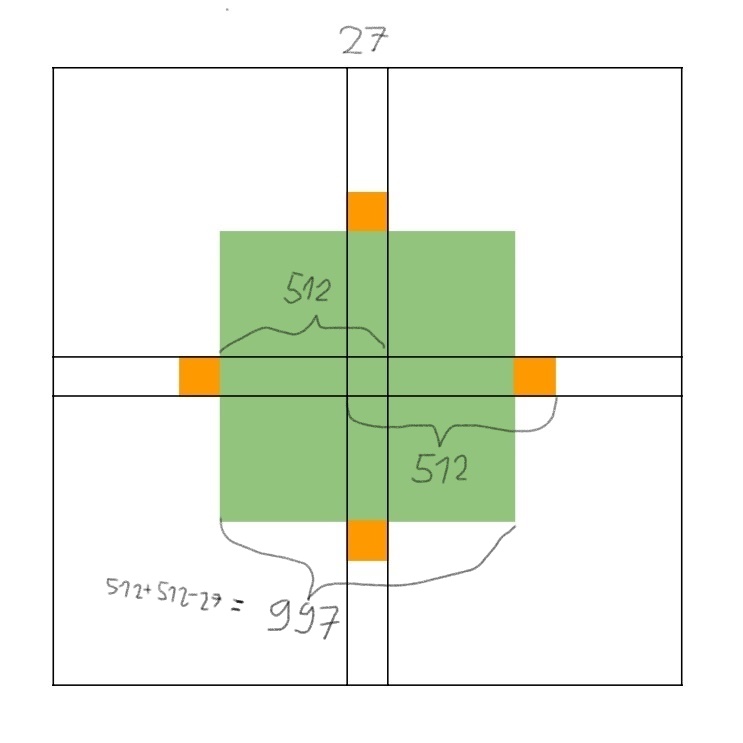
Ak sa stráž nachádza v jednom z modrých štvrococh v rohoch, tiež sa vie pohnúť tak, aby v ňom ostala. Strana týchto štvorcov je znova 997.
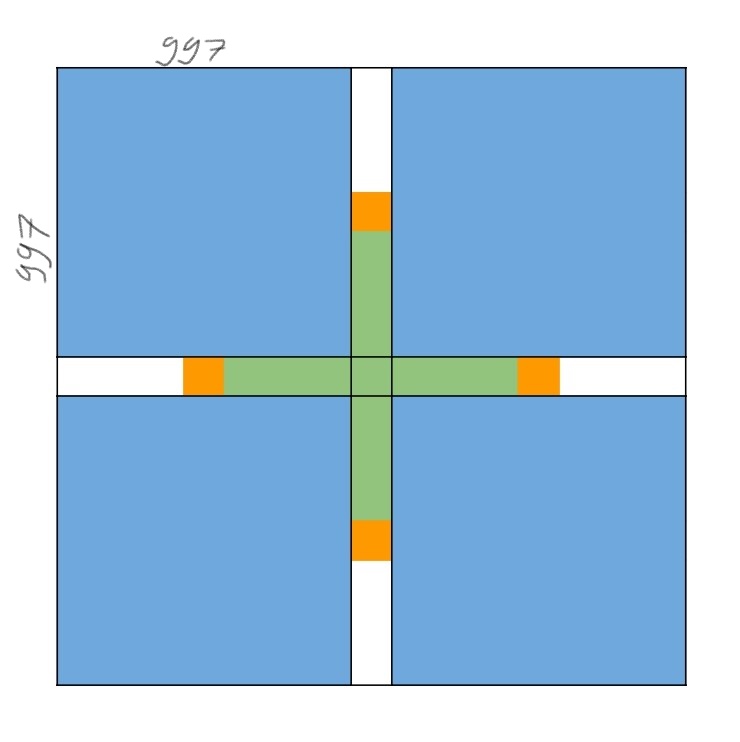
Z fialových obdĺžnikov sa môže pohnúť hore (997\geq256) a zo žltých doľava (997\geq256).
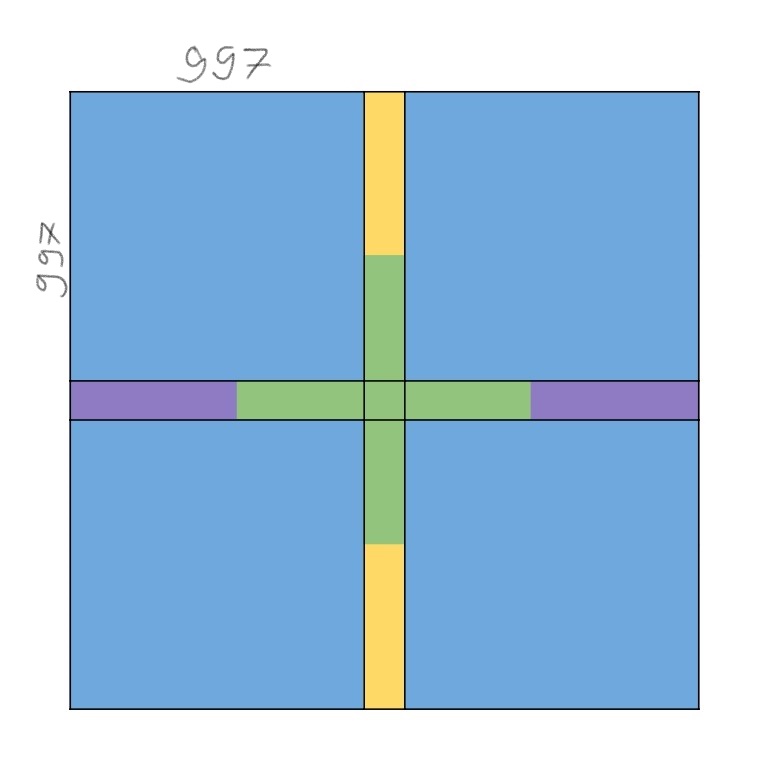
Keď stráž podľa tohto zahrá svoj 9. ťah, Turbanovci sa nebudú vedieť pohnúť do stredového štvorca a stráž bude vedieť zahrať 11. ťah. Turbanovci potom prehrajú, lebo nebudú vedieť zahrať 12. ťah.
Stráž teda má takúto víťaznú stratégiu.
Iné riešenie
Tak isto ako v predchádzajúcom riešení dokážeme, že na 12. ťahu Turbanovci zaručene prehrajú.
Stratégia pre stráž bude takáto: Prvý ťah zahrá ľubovoľne a každý ďalší ťah pôjde opačným smerom ako Turbanovci.
Takýmto spôsobom sa kameň pohne:
- V 1. ťahu o 1
- V 2. a 3. dokopy o 2 (4-2).
- V 4. a 5. dokopy o 8 (16-8).
- V 6. a 7. dokopy o 32 (64-32).
- V 8. a 9. dokopy o 128 (256-128).
- V 10. a 11. dokopy o 512 (1024-512).
To znamená, že po ťahu stráže, bude kameň najďalej 1+2+8+32+128+512=683 políčok od stredu. Na to, aby "vyšla zo šachovnice" by sa musela pohnúť aspoň o 1011, čo je viac ako 683. Vďaka tomu do 11. ťahu určite neprehrá a na 12. ťahu vieme, že prehrajú Turbanovci.
9. príklad
Zadanie
Vzorové riešenie
Ako prvé si všimnime, že naše trojuholníky majú spoločnú stranu. Vieme, že obsah trojuholníka vypočítame ako \frac{1}{2} \cdot a \cdot v_a, kde a je niektorá strana a v_a je výška na ňu. Trojuholníky ABC a BCD majú spoločnú stranu BC a rovnaký obsah. Výška na túto stranu teda musí byť rovnaká. Inými slovami, body A a D musia byť v rovnakej vzdialenosti od BC, a teda priamky AD a BC sú rovnobežné.
Rovnaký postup vieme použiť aj na dvojice trojuholníkov BCD,\, CDE a CDE,\, DEA. Dostaneme tak rovnobežné dvojice CD \parallel BE a DE \parallel CA.

Vráťme sa k zadaniu. Našou úlohou je zistiť niečo o úsečkách BM a NE. Skúsme sa teda zamerať na naše znalosti o bodoch M a N. Oba ležia na úsečke BE, o ktorej vieme, že je rovnobežná s CD. Navyše si môžeme všimnúť, že MC je rovnobežná s DE a ND je rovnobežná s BC. Ľahko si všimneme, že útvary MCDE a NBCD sú rovnobežníky.

O rovnobežníkoch vieme, že ich protiľahlé strany sú rovnko dlhé. To nám konečne dáva nejakú znalosť o dĺžkach úsečiek. Konkrétne dostaneme |ME| = |CD| (z rovnobežníka MCDE) a |NB| = |CD| (z rovnobežníka NBCD). Ich spojením dostaneme |ME| = |NB|. Zostáva už len uvedomiť si, že tieto dve úsečky majú spoločnú časť MN. Jej odčítaním dostaneme |NE| = |MB|, čo sme chceli dokázať.
Komentár
Riešenia mali väčšinou buď malé chyby, alebo boli úplne nesprávne. Veľmi často ste prišli na to, že pravidelný päťuholník zrejme spĺňa aj podmienky zo zadania, aj požadovanú rovnosť, a snažili ste sa ukázať, že ABCDE musí byť vždy pravidelný. To však naozaj platiť nemusí, ako môžete vidieť aj na obrázkoch vyššie. Takéto riešenia body zväčša nedostávali, pokiaľ neodhalili aspoň niektorú rovnobežnosť, ktorá viedla k správnemu riešeniu.
10. príklad
Zadanie
Vzorové riešenie
Vidíme, že v postupnosti sú dôležité štvorice po sebe idúcich čísel, lebo na základe nich vieme, ako bude postupnosť pokračovať. Namiesto toho, aby sme sa pozerali na jednotlivé členy postupnosti osobitne, pozrime sa teda na postupnosť týchto štvoríc. Prvá štvorica je (1, 2, 3, 4), ako nám hovorí zadanie. Ďalšia štvorica bude začínať 2, 3, 4 a nakoniec v nej bude nasledujúce číslo v postupnosti, čo je 0. Druhá štvorica teda bude (2, 3, 4, 0), tretia (3, 4, 0, 9), a tak ďalej.
Každú štvoricu v postupnosti vieme jednoznačne určiť zo štvorice, ktorá je v postupnosti pred ňou. Keď máme štvoricu (a, b, c, d) a za ňou (b, c, d, e), tak e = a + b + c + d - k \cdot 10, kde k si vyberieme tak, aby bolo 0 \leq e < 10 (čiže máme iba jednu možnosť). Z toho vyplýva ďalšia dôležitá vec: z každej štvorice vieme jednoznačne určiť, aká štvorica musí byť v postupnosti pred ňou. Poslednú rovnicu si vieme upraviť na a = e - b - c - d + k \cdot 10, kde k je znova jednoznačne dané.
Rôznych štvoríc je len konečne veľa, takže sa nám niekedy v postupnosti musí vyskytnúť taká, ktorá tam už bola predtým. Pozrime sa na prvú takúto (zopakovanú) štvoricu, ktorá sa v postupnosti vyskytne. Štvorica pred ňou musí byť rovnaká ako štvorica pred jej prvým výskytom. To ale nemôže byť, lebo potom by táto štvorica nebola prvá v poradí, čo sa zopakuje. Prvý výskyt tejto štvorice teda musí byť na začiatku postupnosti, aby pred ním nebola žiadna ďalšia štvorica, a tým pádom to musí byť (1, 2, 3, 4). To znamená, že 1, 2, 3, 4 sa v postupnosti určite zopakuje.
Bude tam 2, 3, 5, 7?Nič nenasvedčuje tomu, že by tam zrovna takáto štvorica mala byť, poďme teda skúsiť dokázať, že nebude. Asi by bolo ťažké vylúčiť práve túto konkrétnu štvoricu, tak na nej môžeme skúsiť nájsť nejakú všeobecnejšiu vlastnosť, o ktorej budeme vedieť, že ju štvorice v postupnosti nemôžu mať.
Postupnosť si môžeme zjednodušiť napríklad tak, že sa budeme pozerať len na paritu čísel v nej. Vďaka parite po sebe idúcich čísel vieme určiť aj paritu nasledujúceho. Postupnosť teda bude vyzerať takto (0 znamená párne, 1 nepárne):
\displaystyle 1, 0, 1, 0, 0, 1, 0, 1, 0, \dots
Vidíme, že sa nám rýchlo zopakuje štvorica (1, 0, 1, 0), takže odvtedy sa bude v postupnosti opakovať stále to isté. Pritom (2, 3, 5, 7) má parity (0, 1, 1, 1), a to sa v tejto postupnosti nenachádza. V pôvodnej postupnosti sa teda takisto nemôže nachádzať ani 2, 3, 5, 7.
Komentár
Veľa z Vás, vyriešilo príklad vypisovaním, či už manuálnym alebo za pomoci programovania. Musím preto pochváliť tých, ktorí sa rozhodli riešiť príklad práve matematicky.
Prémia 1
Zadanie
Vzorové riešenie
Riešenie
Najlepšie riešenie, ktoré sa vám podarilo nájsť, vyzeralo takto:

Sčítaním všetkých kameňov dostávame súčet 1054.
Bodovanie
Riešenia boli obodované podľa súčtu všetkých kameňov podľa nasledovnej škály:
- Súčet vyšší ako 1050 - 8 bodov,
- súčet 1000 až 1050 - 7 bodov,
- súčet 850 až 1000 - 6 bodov,
- súčet 825 až 850 - 5 bodov,
- súčet 750 až 825 - 4 body,
- súčet 675 až 750 - 3 body,
- súčet 200 až 675 - 2 body,
- súčet menej ako 200 - 1 bod.




