Odporúčaný článok

Riešky výlet - Ahojte Rieškari, zoberte batohy, úsmevy, dobré nálady, lopty, hry, frisbee, kamarátov… a poďte s nami na výlet! Poprechádzame sa po Malých Karpatoch, kde pre vás máme pripravený skvelý program a … Prejsť na článok

×

8. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Kráľ Danko mal na kráľovskom dvore vyrytú šachovnicu s 2021\times2021 políčkami. Na políčku presne v strede šachovnice sa nachádza obrovský kameň, ktorý najprv stráž posunie o jedno políčko (rovnobežne so stranami šachovnice). Bratia Turbanovci ho potom budú musieť posunúť o dve políčka nejakým smerom, stráž o štyri políčka, Turbanovci o osem políčok a takto vždy dva krát ďalej – teda v k-tom ťahu ho vždy budú musieť posunúť o 2^{k-1} políčok jedným smerom. Ten, kto je na ťahu, prehráva, ak už nemôže posunúť kameň. Nájdite víťaznú stratégiu (spôsob akým sa dá zaručene vyhrať, bez ohľadu na to ako bude hrať súper) pre bratov Turbanovcov alebo pre stráž.

Vzorové riešenie

Opravovali: matejUuu

V 12. ťahu by sa Turbanovci museli pohnúť 2048 políčok. Keďže na šachovnici nie sú žiadne dve políčka vzdialené 2048, zaručene prehrajú.

Naopak, až do 10. ťahu sa každý určite bude vedieť pohnúť. V týchto ťahoch sa hýbu najviac o 512. Ak by sa nevedeli pohnúť ani doľava ani doprava, znamenalo by to, že naľavo aj napravo od nich je najviac 511 políčok (to isté platí o smeroch hore, dole). To by znamenalo, že tabuľka má na šírku (a výšku) najviac 511+1+511=1023 políčok, čo nie je pravda. Všeobecne platí, že sa určite vieme pohnúť o x vo štvorci so stranou aspoň 2x. Toto využijeme aj neskôr v riešení.

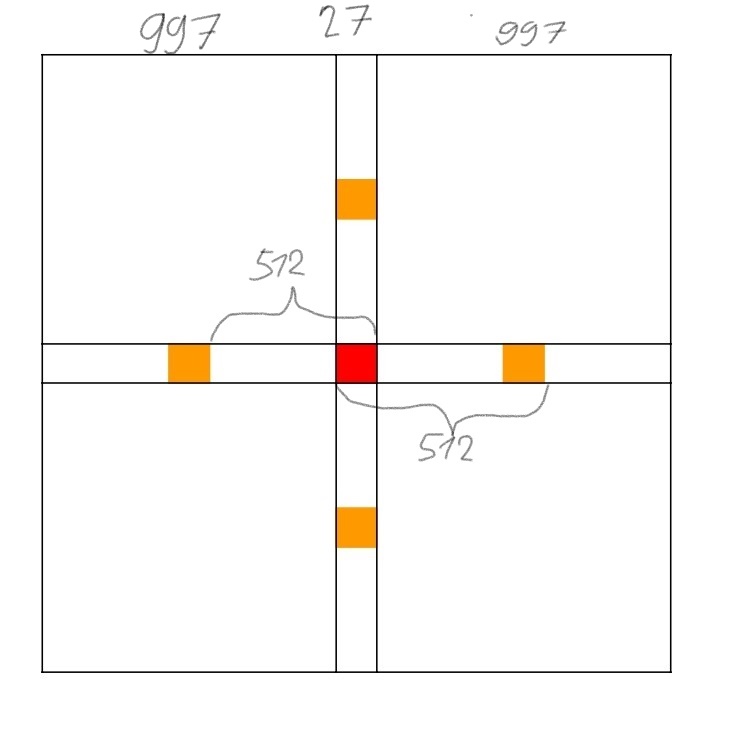
Rozhodujúce teda je len to, či sa stráži podarí v 11. ťahu pohnúť. Na to aby sa mohla pohnúť doprava, musí mať napravo od seba aspoň 1024 políčok, teda musí byť v stĺpcoch 1 až 997 (2021-1024=997). Aby sa mohla pohnúť doľava musí mať naľavo od seba aspoň 1024 políčok, teda musí byť v stĺpcoch 1025 až 2021. Zostávajú teda stĺpce 998 až 1024, z ktorých sa nedá pohnúť ani doľava ani doprava. Tak isto riadky, z ktorých sa nedá pohnúť anu hore ani dole, sú 998 až 1024. To nám vytvára jeden štvorec 27\times 27 v strede šachovnice (červený štvorec).

Aby Turbanovci vyhrali, museli by sa v 10. ťahu pohnúť do tohto štvorca. Tam sa dokážu dostať zo štyroch štvorcoch, jeden v každom smere, posunutých o 512 políčok oproti červenému štvorcu (oranžové štvorce).

Ukážeme, že stráž dokáže zabrániť tomu aby sa Turbanovci nachádzali na začiatku 10. ťahu v ľubovoľnom z týchto štvorcov.

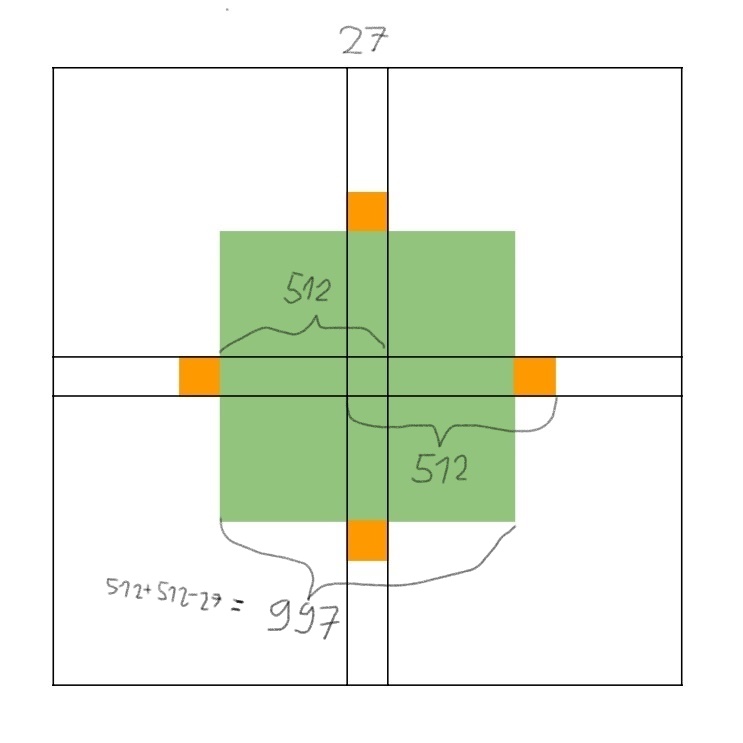
Ak sa stráž na začiatku 9. ťahu nachádza v zelenom štvorci v strede, pohne sa tak, aby v ňom zostala. Strana tohto štvorca je 512+512-27=997, teda určite sa tak bude vedieť pohnúť lebo 997\geq 2\cdot 256.

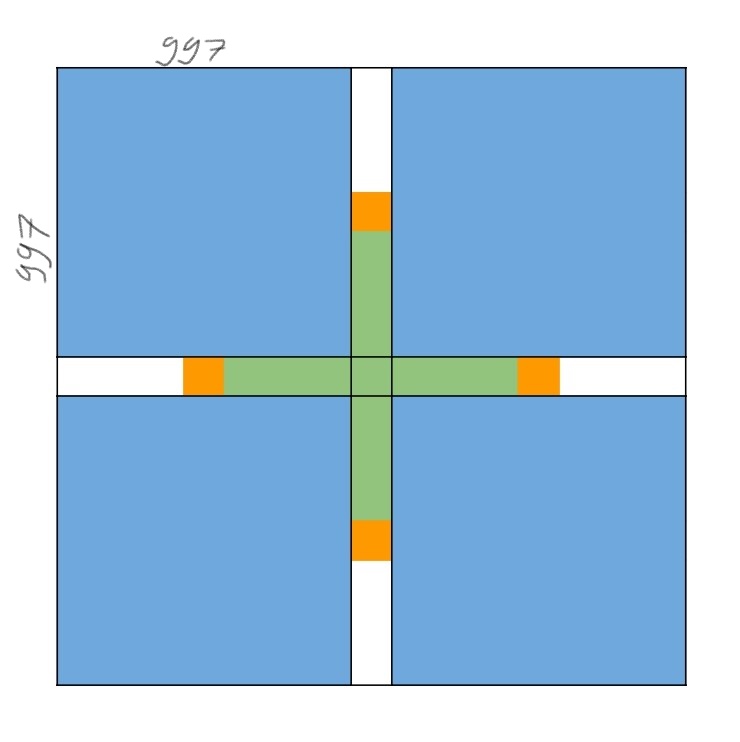
Ak sa stráž nachádza v jednom z modrých štvrococh v rohoch, tiež sa vie pohnúť tak, aby v ňom ostala. Strana týchto štvorcov je znova 997.

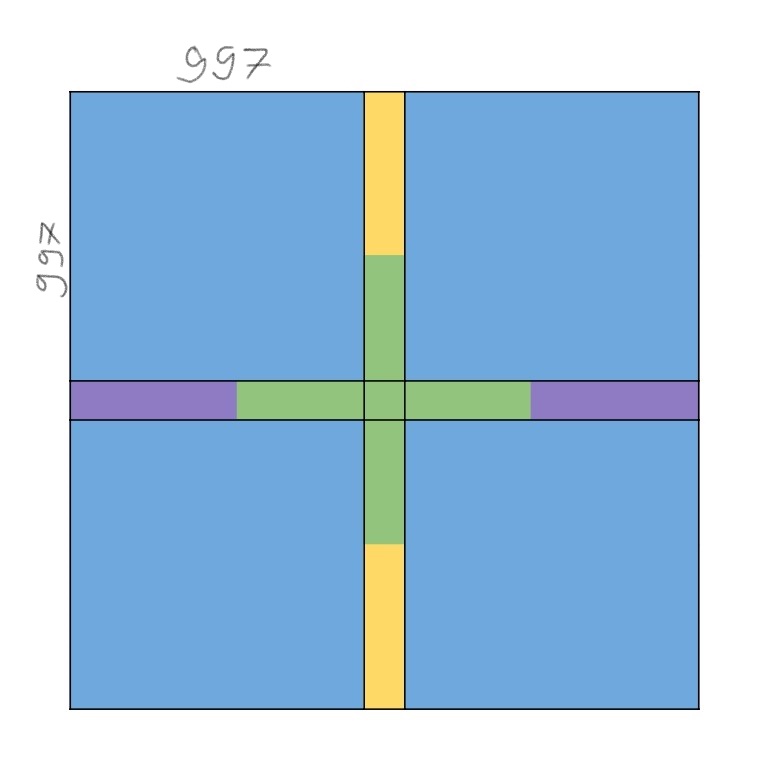
Z fialových obdĺžnikov sa môže pohnúť hore (997\geq256) a zo žltých doľava (997\geq256).

Keď stráž podľa tohto zahrá svoj 9. ťah, Turbanovci sa nebudú vedieť pohnúť do stredového štvorca a stráž bude vedieť zahrať 11. ťah. Turbanovci potom prehrajú, lebo nebudú vedieť zahrať 12. ťah.

Stráž teda má takúto víťaznú stratégiu.

Iné riešenie

Tak isto ako v predchádzajúcom riešení dokážeme, že na 12. ťahu Turbanovci zaručene prehrajú.

Stratégia pre stráž bude takáto: Prvý ťah zahrá ľubovoľne a každý ďalší ťah pôjde opačným smerom ako Turbanovci.

Takýmto spôsobom sa kameň pohne:

  • V 1. ťahu o 1
  • V 2. a 3. dokopy o 2 (4-2).
  • V 4. a 5. dokopy o 8 (16-8).
  • V 6. a 7. dokopy o 32 (64-32).
  • V 8. a 9. dokopy o 128 (256-128).
  • V 10. a 11. dokopy o 512 (1024-512).

To znamená, že po ťahu stráže, bude kameň najďalej 1+2+8+32+128+512=683 políčok od stredu. Na to, aby "vyšla zo šachovnice" by sa musela pohnúť aspoň o 1011, čo je viac ako 683. Vďaka tomu do 11. ťahu určite neprehrá a na 12. ťahu vieme, že prehrajú Turbanovci.