Letný tábor 2025 - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×1. príklad
Zadanie
Vzorové riešenie
Vieme, že po nejakom kole mala Ena priemer 176 a po kole so ziskom 185 bodov, sa jej priemer zväčšil o jedna na 177. Zistime si teda koľko kôl Mentorovej hry prebehlo po tom, ako hodila 185 bodov.
Kolo, v ktorom získala týchto 185 bodov, musí byť deviate. To preto, lebo získala 9 bodov navyše oproti priemeru bodov po predošlom kole. Aby sa priemer zväčšil práve o 1, tak sa musí týchto 9 bodov rozrátať po jednom do každého kola. 185 bodov teda hodila v 9. kole.
Otázkou ale je, koľko bodov musí získať v ďalšom, teda desiatom, kole, aby sa jej priemer zdvihol na 178 bodov. To si vypočítame tak, že od celkového počtu bodov po desiatom kole odpočítame počet bodov po deviatom kole. Tieto počty vieme zistiť tak, že priemer po danom kole vynásobíme číslom kola.
178 \cdot 10 - 177 \cdot 9 = 187
Ena potrebuje hodiť 187 bodov v ďalšom kole, aby sa jej priemer zvýšil na 178.
2. príklad
Zadanie
Vzorové riešenie
Súčtom spomínaných 3 zaokrúhlených čísel má byť 4-ciferné číslo 5730. Z toho vyplýva, že žiadny zo sčítancov nemôže byť 5-ciferný. Aj 3-ciferné čísla môžeme vylúčiť, pretože ani najväčšie 3-ciferné číslo sa v súčte pri našom spôsobe zaokrúhlovania nevyšplhá na 5730.
999 \Rightarrow 1000 + 1000 + 1000 = 3000 < 5730
Vďaka tomu môžeme využiť grafický zápis sčítania čísel pod sebou a pre jednotlivé cifry si zadefinujeme nasledovné:
- Cifry čísla, ktoré bolo zaokrúhlené na desiatky si označíme ako A,\,B,\,C a 0 (keďže je zaokrúhlené na desiatky, posledná cifra bude určite práve 0).
- Cifry čísla zaokrúhleného na stovky označíme D,\,E,\,0,\,0 (zase, posledné dve cifry musia byť 0 keďže hovoríme o čísle zaokrúhlenom na stovky).
- Cifry čísla zaokrúhleného na tisícky označíme F,\,0,\,0,\,0.
| A | B | C | 0 |
| D | E | 0 | 0 |
| F | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
Teraz sa pozrieme, aké čísla by sme vedeli doplniť za A,\,B,\,C,\,D,\,E a F, s tým, že budeme používať pravidlá sčítania čísel pod sebou. Vidíme, že pri sčítaní posledných cifier sčítancov dostaneme 0 a nezostane nám nič na prenos do ďalšieho rádu. To znamená, že C + 0 + 0 \left(+0\right) = C je číslo, ktoré končí cifrou 3. Keďže C sa môže skladať iba z jednej cifry, musí ísť o cifru 3.
Vidíme teda, že
| A | B | 3 | 0 |
| D | E | 0 | 0 |
| F | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
Na mieste stoviek je to ale trochu komplikovanejšie, súčet cifier B a E totiž môže byť 7, ale aj 17, aby sme si stále mohli podpísať pod ne cifru 7 v čísle 5730. Väčšie čísla končiace na 7čku nemá zmysel zvažovať, lebo väčší súčet ako 18 súčtom dvoch cifier nedosiahneme. Okrem toho medzi ciframi B a E musí platiť vzťah, že B sa zaokrúhli nahor skrz zaokrúhľovanie na stovky na cifru E alebo v prípade cifry 9 na číslo 10 a teda na 0, s tým, že v takom prípade ovplyvní aj miesta tisícok (D a F). Tento špeciálny prípad, ale môžeme vylúčiť, lebo ak B = 9 a E = 0, tak B+E nekončí na cifru 7. Preto môžeme bezpečne tvrdiť, že vďaka zaokrúhlovaniu platí E = B + 1.
Zvažujeme teda dve možnosti pre B a E:
B + E = 7
B + B + 1 = 7
B = 3, E = 4
prenášame 0 do ďalšieho rádu
\newline
| A | 3 | 3 | 0 |
| D | 4 | 0 | 0 |
| F | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
B + E = 17
B + B + 1 = 17
B = 8, E = 9
prenášame 1 do ďalšieho rádu
\newline
| A | 8 | 3 | 0 |
| D | 9 | 0 | 0 |
| F | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
Presuňme sa teda do rádov tisícov. V oboch prípadoch nemôžeme pri sčítaní tisícok \left(A + D + F + prenos\right) prenášať do ďalšieho rádu žiadne jednotky, pretože výsledok končí v ráde tisícov, konkrétne cifrou 5. Z toho vieme jednoznačne tvrdiť, že A = 1, pretože ak by A bolo väčšie, tak aj D a F by boli aspoň tak veľké a \left(2+\right) + \left(2+\right) + \left(2+\right) \geq 6 > 5. Ak A = 1, tak D = 1 a F = 2, pretože pri zaokrúhlení na tisícky sa musí zvýšiť o 1.
| 1 | B | 3 | 0 |
| 1 | E | 0 | 0 |
| 2 | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
Tu je vidieť, že jediná možnosť pre B a E je 8 a 9, pretože inak by nám nesedel súčet v ráde tisícov, kde nám chýba 1 do súčtu 5.
| 1 | 8 | 3 | 0 |
| 1 | 9 | 0 | 0 |
| 2 | 0 | 0 | 0 |
| 5 | 7 | 3 | 0 |
Ako vidíme, všetky súčty sedia a už nám ostáva len zistiť pôvodné číslo. Sčítanec 1830 je najbližšie pôvodnému číslu, pretože je zaokrúhlený iba na desiatky a zároveň vieme, že žiadna, teda ani posledná cifra pôvodného čísla nie je 0. Keďže je pravidlom, že zaokrúhľujeme vždy nahor, cifra na mieste desiatok bude 3 - 1 = 2. Aká môže byť posledná cifra?
Odpoveď: Tu sa vyskytli medzi riešeniami rôzne výklady zadania. Niektorí pochopili to, že posledná cifra je najmenšia tak, že je menšia ako všetky ostatné. Vtedy keďže je prvá cifra 1, posledná cifra by musela byť 0, čo zo zadania nemôže byť, úloha teda nemá riešenie.
Druhou možnosťou je, že nesmie byť v čísle cifra menšia ako tá posledná, vtedy existuje riešenie práve jedno a to 1821. Pre nejasnosť zadania sme uznávali oba výsledky.
Komentár
Poslednú časť príkladu, teda určenie poslednej cifry pochopili riešitelia veľmi rôzne. Častou chybou bola kombinácia dvoch spôsobov spomenutých v riešení. Po doplnení cifry 2 na miesto desiatok povedali, že posledná cifra musí byť menšia, teda 1. Keď neskôr ukázali že prvá cifra je 1, neoverili či je posledná stále menšia ako nová najmenšia.
Pokiaľ sme úlohu riešili tak že posledná cifra musí byť menšia ako všetky ostatné, stačilo sa dopracovať k tomu že prvá cifra pôvodného čísla musí byť 1 a tým pádom úloha nemá riešenie.
Druhou chybou, ktorú stojí za to spomenúť, je možnosť cifry 9 v pôvodnom čísle. Tá, ako je ukázané vyššie v riešení, vie totiž niekedy robiť nepredvídateľné veci. Niektoré postupy túto úvahu nepotrebovali, v niektorých chýbala.
3. príklad
Zadanie
Vzorové riešenie
Ako prvé sa pozrieme na prvé dve informácie, ktoré nám zadanie dáva. Z toho, že pán zo stánku to má k Obrovi ďalej, ako ku Klausovi vieme, že Obor nemôže bývať medzi ním a Klausom, teda v strede. Podobne vieme, že Obor to má ku Klausovi bližšie ako k pánovi zo stánku, a preto ani pán zo stánku nemôže bývať medzi ostatnými dvoma. Jediný z trojice, ktorý teda môže bývať v strede, je Klaus.
Po zapísaní si číselných údajov teda vieme, že pán zo stánku to má medzi Klausom a Obrom ešte 360 svojich krokov, a Obor to má medzi Klausom a pánom zo stánku ešte 120 svojich krokov. Ešte poznáme počet krokov, ktorý prešiel Klaus, keď išiel k Obrovi, potom k pánovi zo stánku a od neho naspäť domov. Vzdialenosti ktoré prešiel si zapíšeme tak, že vzdialenosť medzi dvoma domami značíme začiatočnými písmenami majiteľov, a malé písmeno značí krok danej osoby.
600k = KO+OP+PK
Vieme však, že pri tom ako išiel od Obra k pánovi zo stánku prešiel okolo svojho domu, keďže je medzi nimi a teda si vieme túto vzdialenosť rozdeliť na dve:
\hspace{2cm} 600k = KO+OK+KP+PK=2OK+2KP \hspace{1cm} /:2 \\300k = OK + KP
Teda Klaus vlastne prešiel celú ulicu 600 krokmi dvakrát, a teda raz ju prejde 300 krokmi. A tieto vzdialenosti v rámci ulice síce poznáme v iných krokoch ako Klausových, ale napriek tomu si ich môžeme doplniť:
300k = 360p + 120o
Vieme ešte, že Klausove kroky sú dvakrát dlhšie ako kroky pána zo stánku, a preto na vzdialenosti OK by ich Klaus spravil dvakrát menej. Aj to si doplníme do našej rovnice:
\hspace{2cm} 300k = 180k + 120o \hspace{1cm} /-180k \\120k = 120o
Keď odčítame z oboch strán 180 Klausových krokov, teda to čo prejde na vzdialenosti OK, tak zisťujeme že na vzdialenosti KP urobí aj Obor aj Klaus 120 krokov, a teda ich kroky sú rovnaké. Ak teda chceme zistiť, koľko krokov urobí Obor medzi ním a pánom zo stánku, bude to rovnako ako ich spraví Klaus. A o Klausovi už vieme, že celú ulicu, na ktorej koncoch bývajú Obor a pán zo stánku prejde 300 krokmi.
Odpoveď: Klaus býva uprostred, a Obor spraví 300 krokov, keď ide na návštevu k pánovi zo stánku.
4. príklad
Zadanie
Klausova šachovnica má tvar ôsmych políčok vedľa seba a každý hráč má tri figúrky: kráľa (K), jazdca (J) a vežu (V). Na obrázku vidíte ich počiatočné rozostavenie.

Každá figúrka sa môže pohybovať aj doľava aj doprava, ak má k dispozícií vhodné miesto. Každý ťah musí smerovať buď na prázdne políčko alebo na políčko obsadené súperovou figúrkou, ktorú tým pádom vyhodí a odstraňuje sa zo šachovnice. Kráľ sa môže pohybovať vždy len o jedno políčko a nesmie sa ťahom dostať do „šachu“ – na políčko ohrozené súperom. Jazdec sa pohybuje o dve políčka vpravo alebo o dve políčka vľavo, pričom políčko uprostred preskakuje. Veža sa môže posunúť o ľubovoľný počet políčok, pričom nemôže prejsť cez obsadené políčko. Ani po pohybe týchto figúrok nesmie byť kráľ ohrozený súperom.
Kráľ:
Jazdec:

Veža:

Ak hráčovi nezostáva žiaden prípustný ťah, hra končí remízou. Hráč, ktorý ohrozí súperovho kráľa tak, že kráľ nemá kam utiecť, dal mat a vyhráva. Začína biely. Dokáže niektorý hráč zabezpečiť, aby vyhral, bez ohľadu na to, ako hrá súper? Ak áno, určte ktorý a ako to docieli. Ak nie, vysvetlite prečo.
Vzorové riešenie
Najskôr si uvedomíme čo víťazná stratégia je. Je to nejaká postupnosť ťahov, ktorú musíme vykonať aby sme zaručene vyhrali bez ohľadu na to ako hrá náš súper.


Vieme, že čierny víťaznú stratégiu nemôže mať, lebo keď biely spraví prvý ťah na políčko 6 vežou (vyhodí tým čiernemu vežu) tak čierny nemá žiadne možnosti kam sa pohnúť a zároveň jeho kráľ nie je ohrozený — nastáva remíza.

Tak poďme teraz ukázať, že za bieleho vieme nájsť víťaznú stratégiu. To sa nám podarí, ak spraví prvý pohyb jazdcom na 4. políčko.

Ak biely spraví prvý pohyb jazdcom, čierny má 3 možnosti ťahov: pohne vežou na 4. políčko a vyhodí nám jazdca, pohne vežou na 5. políčko alebo naň presunie jazdca. Poďme si ich teda všetky vyskúšať:

- čierny pohne vežou na 4. políčko a vyhodí nám jazdca.
- čierny pohne vežou na 5. políčko.
- čierny sa pohne jazdcom na 5. políčko
My teraz vyhodíme našou vežou čiernu vežu a čierny má len jeden možný pohyb a to jazdcom na 5. políčko. Po tomto ťahu mu ho však môžeme vyhodiť a vyhrali sme.




Teraz pohneme vežou na 2. políčko. Čierny má na výber 2 ťahy. Buď nám vyhodí vežou jazdca alebo sa pohne na 6. políčko. Musíme si ich oba overiť.


Ak nám vyhodí jazdca tak my mu teraz vyhodíme vežu našou vežou. Čierny môže ísť teda jedine jazdcom a to na políčko 5. My mu ho následne vyhodíme vežou a vyhráme.




Ak sa pohne vežou na 6. políčko tak my mu ju vyhodíme jazdcom a zároveň dáme mat čiernemu a vyhráme.


Potom mu vyhodíme jazdcom vežu a dáme tak šach. Čierny sa teraz musí dostať preč zo šachu a to jedine tak, že pohne kráľa na 7. políčko. Teraz pohneme vežu na 4. políčko a čierny má momentálne dve možnosti: Buď vezme kráľom jazdca alebo pohne jazdcom na 3. políčko.




Ak nám kráľom vezme jazdca, my sa pohneme kráľom na druhé políčko. Jediný pohyb, ktorý vie čierny vykonať je posunúť kráľa na 7. políčko, my vyhodíme jazdca na 5. políčku vežou a dáme mu mat.




Ak pohne jazdcom na 3. políčko, tak náš kráľ je v šachu. My sa ním uhneme na 2. políčko. Čiernemu ostávajú dve možnosti, buď sa pohnúť jazdcom na políčko 1 alebo na políčko 5.


Ak sa pohne na políčko 1 tak my sa posunieme jazdcom na políčko 8 a dáme čiernemu mat.


Ak sa však pohne na políčko 5 tak to nie je o moc lepšie. Pohneme naším jazdcom na políčko 8. Čierny môže urobiť len jediný možný ťah a to kráľom vyhodiť nášho jazdca na 8. políčku. My mu vyhodíme vežou jazdca a dáme mu mat.




Takto sme si ukázali, že keď biely spraví prvý ťah jazdcom tak vo všetkých možných prípadoch vyhrá – našli sme výhernú stratégiu.
5. príklad
Zadanie

Vzorové riešenie
1. spôsob
Najprv si označíme čísla v jednotlivých krúžkoch a až g ako na obrázku:
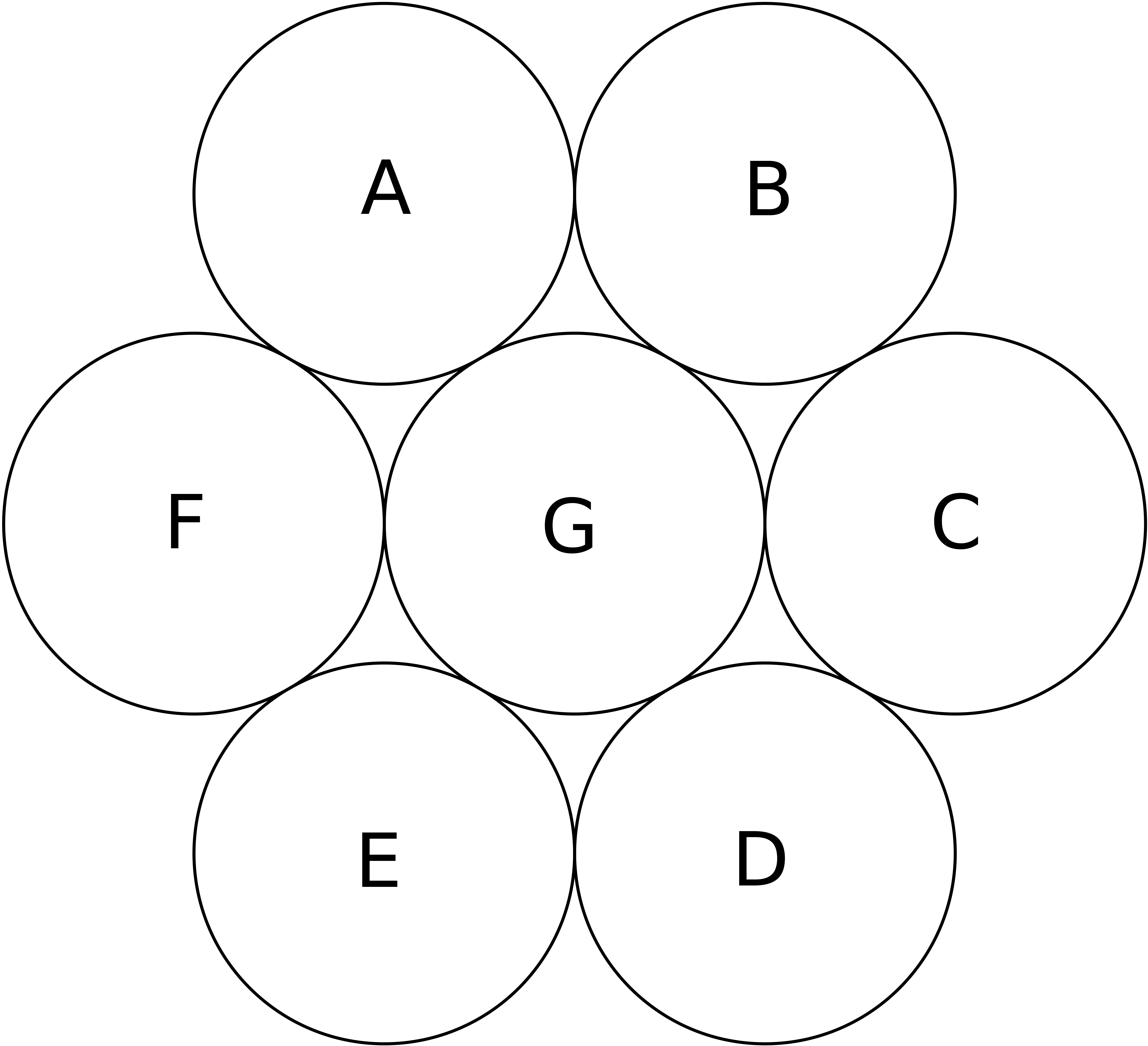
Pozrime sa teraz na súčty susedov krúžkov s číslom a a c. Zo zadania vieme, že tieto súčty musia byť rovnaké a teda dostávame: f+g+b=b+g+d. Po odčítaní g+b z oboch strán, dostávame f = d. Rovnakým postupom vieme dostať aj rovnice f = b, b = d, a = c, c = e a e = a. Keď tieto rovnice spojíme, dostaneme a = b = c a b = d = f.
Teraz sa pozrieme na súčty susedov krúžkov s číslom a a b. Dostávame rovnicu f+g+b = a+g+c. Keďže ako vieme, že a = c a f = b, túto rovnicu si vieme prepísať na 2b + g = 2a + g, teda b = a.
Z toho vyplýva, že všetky čísla na okraji sú rovnaké. Čísla v nich si označme a. Okolo stredného krúžku máme teraz súčet 6a a okolo jedného z okrajových krúžkov máme súčet 2a + g. Teda 6a = 2a + g, z čoho výplíva, že g = 4a.
Keďže máme čísla v každom krúžku vyjadrené pomocou a, tak ak za a dosadíme najmenšie prirodzené číslo, teda 1, tak dostaneme najmenší možný výsledok, ktorý je teda 6.
Výhodou tohto riešenia je, že je všeobecnejšie. Napríklad je pekne vidieť, že výsledok bude násobkom čísla 6, keďže je v tvare 6a. Taktiež keby sa nás niekto pýtal aký je 42. najmenší výsledok, tak nemáme problém za a dosadiť 42 a víde nám 252, pričom pri použití 2. spôsobu nám tieto pekné vlastnosti príkladu pravdepodobne uniknú.
2. spôsob
Pozrime sa na stredný krúžok. Dotýka sa ho 6 krúžkov. Teda najmenší možný súčet, ktorý môžeme dostať je 6, a to vtedy, keď budú všade na okraji najmenšie možné čísla, teda jednotky.
Riešenie, kde je výsledok 6 je napríklad takéto:

Keďže sme si ale dokázali, že výsledok je najmenej 6, toto je najmenšie možné riešenie.
Komentár
Väčšina z vás vyriešila tento príklad bez problémov druhým spôsobom. Veľmi chválime ľudí, ktorí si dali prácu navyše a našli tu odprezentované prvé riešenia. Chýb nebolo veľa, no keď sa našli, väčšinou ste nezdôvodnili, prečo by čísla v okolitých krúžkoch mali byť navzájom rovnaké a potom ste na tom stavali. V prvom riešení si môžete všimnúť ako sa to dalo pekne zdôvodniť. Pri tom druhom je dôležité, že preň nepotrebujeme povedať, že všetky okolité čísla musia byť rovnaké. Stačí nám, že nech sú hocijaké, tak najmenšie prirodzené číslo, ktoré do každého okienka môžeme dať je 1. Aj ak by boli tie čísla rôzne, tak by bol súčet väčší.
6. príklad
Zadanie
- Je deliteľné číslom 13.
- Jeho prvé aj posledné dvojčíslie sú dvojciferné prvočísla.
- Ak sčítame prvé a posledné dvojčíslie, dostaneme druhú mocninou nejakého celého čísla.
- Cifra na mieste stoviek je o 4 menšia ako najväčšia cifra (alebo cifry).
- Ciferný súčin je deliteľný číslom 49.
Poznámka: Druhú mocninu čísla dostaneme tak, že dané číslo vynásobíme sebou samým.
Poznámka 2: Ciferný súčin čísla dostaneme tak, že postupne vynásobíme všetky jeho cifry.
Vzorové riešenie
Označme si hľadaný kód ABCD, kde A, B, C, D sú jeho cifry.
Najprv sa zameriame na 5. podmienku, teda ciferný súčet nášho čísla má byť deliteľný 49.
To znamená, že tento súčin bude 0, alebo väčší násobok 49, takže hľadaný kód bude obsahovať cifru 0 alebo dve cifry 7.
Pozrime sa na to, či v čísle môže byť nejaká cifra 0. Podľa 2. podmienky prvé aj posledné dvojčíslie musia byť dvojcifernými prvočíslami, teda A ani C nemôžu byť nula. Keby B alebo D boli 0, tak takéto číslo by bolo určite násobkom 10, teda by nebolo prvočíslo. Dostávame tak, že v čísle ABCD nemôžu byť nulové cifry.
Takže v čísle musia byť aspoň dve cifry 7. Opäť sa pozrime na 2. podmienku. Keďže 77 nie je prvočíslo (lebo 11 \cdot 7 = 77), tak dvojčíslia AB a CD môžu obsahovať najviac jednu cifru 7. A keďže v čísle ABCD majú byť dve cifry 7, tak bude každé toto dvojčíslie obsahovať práve jednu.
Teraz sa pozrime na 4. podmienku.
Ak by číslo ABCD obsahovalo cifru 9, cifra B by musela byť 5, čo ale je v rozpore s 2. podmienkou, lebo čísla zakončené na 5 sú deliteľné 5. Preto najväčšia cifra nebude 9.
Podobne ak by najväčšia cifra bola 8, tak by B muselo byť 4, čo je opäť v rozpore z podobného dôvodu. Keďže vieme, že číslo ABCD bude obsahovať cifru 7, tak bude najväčšia a dostávame, že B=3. Ako sme spomínali vyššie, dvojčíslie AB musí obsahovať práve jednu 7, teda A=7. Číslo 73 je prvočíslom, teda spĺňa druhú podmienku.
Ešte nám ostala 3. podmienka.
Najmenšie dvojciferné číslo je 10, najväčšie je 99. Teda súčet prvého dvojčíslia, ktoré je 73, a posledného dvojčíslia bude niekde medzi 83 a 172. Druhé mocniny celého čísla v tomto rozsahu sú 100, 121, 144 a 169. Keďže dvojciferné prvočísla sú nepárne a súčet dvoch nepárnych čísel je párny, do úvahy prichádzajú iba 100 a 144. Sú teda dve možnosti:
- ak 73+CD=100, CD=27, ale 27 nie je prvočíslo,
- ak 73+CD=144, CD=71 a 71 je prvočíslo.
Ako posledná nám ostala 1. podmienka, ktorú nesmieme zabudnúť overiť. 7371:13 = 567, zvyšok 0. Číslo ABCD je deliteľné 13.
Overili sme všetky podmienky a vylúčili iné možnosti riešenia.
Odpoveď: Kód od brány je 7371.
Komentár:
Veľa z vás zabudlo na to, že aj 0 je deliteľné 49, niektorí ste zase predpokladali, že číslo obsahuje práve dve cifry 7. Tým sa vám mohlo stať, že vynecháte nejaké riešenia príkladu.
7. príklad
Zadanie
Vzorové riešenie

Zaujímajú nás dva trojuholníky — ABX a DYX. Skúsme si teda vyjadriť ich obsahy. Trojuholník ABX je jednoduchý, jeho základňa je AB, ktorej dĺžku označíme a a miesto výšky vieme použiť ďalšiu stranu obdĺžnika - BC, s dĺžkou b. Obsah tak vyadríme ako \frac{1}{2}ab, čo je polovica obsahu obdĺžnika.
Druhý trojuholník — DYX — je pravouhlý, keďže \measuredangle XDY je zároveň uhlom obdĺžnika. Obsah tak vieme vyjadriť ako \frac{1}{2} |DX| \cdot |DY|. Radi by sme však zistili, ako vyzerá tento obsah vzhľadom k obdĺžniku zo zadania. O trojuholníku ABX už vieme, že je jeho polovicou.
Zamerajme sa teraz na poslednú vlstnosť zo zadania, ktorú sme ešte nepoužili — rovnobežnosť AX a CY. Vidíme, že uhly \measuredangle DCY a \measuredangle DXA sú súhlasné a teda rovnako veľké. To isté sa dá povedať aj o uhloch \measuredangle DYC a DAX. Takže trojuholníky DAX a DYC sú podobné podľa vety uu.
Podobnosť nám okrem iného vraví, že existuje koeficient podobnosti, ktorý označuje pomer dĺžok medzi jednotlivými útvarmi. PRe naše trojuholníky si ho označme k. Platí:
|DC| = k \cdot |DX|,\\ |DY| = k \cdot |DA|.
Odtiaľ vieme vyjadriť k:
k = \dfrac{|DC|}{|DX|} = \dfrac{|DY|}{|DA|} \\ \dfrac{a}{|DX|} = \dfrac{|DY|}{b} \\ ab = |DX| \cdot |DY|
Najprv sme využili a = |DC|,\, b = |DA| a následne sme vynásobili rovnicu b|DX|. Keď už vieme, že |DX| \cdot |DY| = ab, vieme obsah DYX vyjadriť ako \frac{1}{2} ab. Trojuholníky ABX a DYX majú rovnaký obsah.
Odpoveď: Pomer obsahov trojuholníkov ABX a DYX je 1:1.
Iné riešenie (bez podobnosti)
Na začiatok si podobne ako v predošlom riešení vyjadrime obsah trojuholníka ABX. Ten je \frac{1}{2} ab, teda polovica obsahu zadaného obdĺžnika. Z rôznych obrázkov vyzerá, že obsah DYX by mohol byť rovnaký, tak sa pokúsme dokázať to.
Pozrime sa na trojuholník ACD. Strana AC je uhlopriečkou zadaného obdĺžnika, takže ho delí na polovicu. Zároveň si môžeme všimnúť, že celý jeho obsah sa nachádza vnútri trojuholníka DYC, rovnako ako trojuholník DYX. Keď sme si tot všetko všimli nastáva čas využiť rovnobežnosť AX a CY.


Vyššie spomínaný trojuholník DYC vieme rozdeliť na ACD a YCA, alebo na DYX a YCX. Platí:
S_{DYC} = S_{ACD} + S_{YCA} = S_{DYX} + S_{YCX} \\ S_{ACD} - S_{DYX} = S_{YCX} - S_{YCA}
Vidíme teda, že ak majú trojuholníky YCX a YCA rovnaký obsah, majú rovnaký obsah aj DYX a ACD a teda aj ABX.
My vieme, že YC a AX sú rovnobežné. Kolmica z ľubovoľného bodu priamky AC na YC tak bude mať rovnakú dĺžku. Trojuholníky YCX a YCA tak majú okrem spoločnej základne YC aj rovnakú výšku a teda rovnaký obsah. Ako teda už vieme, majú rovnaký obsah aj DYX a ACD. Ten je polovicou obsahu zadaného obdĺžnika, takže rovnaký obsah má i ABX.
Odpoveď: Pomer obsahov trojuholníkov ABX a DYX je 1:1.
Komentár
Väčšina z vás riešila príklad prvým spôsobom a naozaj ste ho viacerí zvládli veľmi pekne. Najčastejšie chyby boli v chýbajúcom vysvetlení, prečo sú trojuholníky podobné. Tu sme vyžadovali prepojiť nejak túto podobnosť s rovnobežnosťou zo zadania, čo ste niektorí nespravili a strácali ste tak bod. Väčšie straty boli často spôsobené chybami v postupe, keď ste sa potrebné vlastnosti dĺžok DX a DY snažili vysvetliť bez podobnosti, väčšinou nesprávne. Existovali viaceré postupy, ktoré nevyžadovali túto vlastnosť (nielen ten vyššie), no tie neboli až tak priamočiare a vyskytovali sa zriedka. Pokiaľ však boli správne, dostali 10 bodov.
8. príklad
Zadanie
Vzorové riešenie
Tento príklad bolo ideálne počítať tak, že sme našli spôsob, ako rýchlo zistiť, či sa pre nejaký počet rozlomených článkov dá odvážiť každý počet gramov. Potom nám stačí vyskúšať rôzne počty rozlomení a nájsť najmenší, ktorý stačí.
Chceme zistiť, či sa to dá, keď rozlomíme 3 články:
Máme teda 3 rozlomené články a najviac 4 kusy reťaze. Dĺžky týchto kusov si určíme tak, aby sme vedeli odvážiť čo najviac rôznych hmotností, ako sa dá.
Pomocou tých troch rozlomených článkov vieme odvážiť hmotnosti 1-3 gramy.
Aby sme vedeli odvážiť 4 gramy, potrebujeme kus reťaze s hmotnosťou najviac 4. Všimnime si, že keď vieme odvážiť všetky hmotnosti po nejaké číslo x a pridáme kus s hmotnosťou y, budeme navyše vedieť odvážiť hmotnosti od y do x+y. Tým pádom by bolo ideálne, aby sa tieto intervaly nikdy neprekrývali - teda aby platilo y>x. Takže najviac rôznych hmotností dosiahneme, ak to bude presne 4.
S reťazou hmotnosti 4 vieme odvážiť 1-7 gramov. To znamená, že ďalšia reťaz bude mať hmotnosť 8.
S reťazami hmotnosti 4 a 8 vieme odvážiť 1-15 gramov. Takže dalšia reťaz bude mať 16 gramov.
S reťazami hmotnosti 4, 8 a 16 vieme odvážiť 1-31 gramov. Posledný štvrtý kus bude mať všetky zvyšné články, teda 150-3\cdot1-4-8-16=119.
S reťazami hmotnosti 4, 8, 16 a 119 vieme odvážiť 1-63 gramov a 119-150 gramov.
To znamená, že pre 3 rozlomenia reťaze vieme navážiť najviac 63 rôznych hodnôt.
Skúsme teda 4:
Máme 4 rozlomené články a najviac 5 kusov reťaze. Znova sa snažíme, aby sme vedeli odvážiť, čo najviac rôznych hmotností.
Pomocou tých štyroch rozbitých článkov vieme odvážiť hmotnosti 1-4 gramy.
Aby sme vedeli odvážiť 5 gramov, jedna z reťazí bude musieť mať hmotnosť 5.
S reťazou hmotnosti 5 vieme odvážiť 1-9 gramov. To znamená, že ďalšia reťaz bude mať hmotnosť 10.
S reťazami hmotnosti 5 a 10 vieme odvážiť 1-19 gramov. Takže dalšia reťaz bude mať 20 gramov.
S reťazami hmotnosti 5, 10 a 20 vieme odvážiť 1-39 gramov. Takže dalšia reťaz bude mať 40 gramov.
S reťazami hmotnosti 5, 10, 20 a 40 vieme odvážiť 1-79 gramov. Posledný, piaty kus bude mať všetky zvyšné články, teda 150-4\cdot1-5-10-20-40=71.
Takto vieme odvážiť 1-79 gramov a s použitím posledého piateho kusu reťaze 71-150 gramov.
Čiže pri 4 rozlomeniach vieme navážiť všetky hmotnosti od 1 do 150 gramov.
A keďže sme si ukázali, že pre 3 to nejde, vieme, že 4 je najmenší počet rozlomení, na ktorý sa to dá.
Iné riešenie:
Ešte by sme radi ukázali iný spôsob, ako sa dá dokázať, že 3 zlomenia nám nestačia. Keď rozlomíme 3 články, získame najviac 7 častí reťaze (3 zlomené a 4 súvislé časti medzi nimi). Pozrime sa, koľko možných kombinácií z nich môžeme vybrať. Každú časť môžeme buď vybrať alebo nevybrať a teda máme 2\cdot2\cdot2\cdot2\cdot2\cdot2\cdot2 alebo 2^7 možností. To nám ale dokopy dáva iba 128 možných kombinácií, teda nie je možné pomocou nich odvážiť 150 rôznych hotností. Takéto riešenie, sa viac podobá na poriadny matematický dôkaz, naopak to prvé riešenie skôr zodpovedá tomu, ako sme pri riešení rozmýšľali.
Komentár:
Veľa z vás si neuvedomilo, že pri zlomení článku získame okrem dvoch súvislích častí reťaze ešte jeden zlomený článok. Potom ste sa snažili použiť klasickú binárnu sústavu, čo ale neviedlo k optimálnemu riešeniu.
9. príklad
Zadanie
Vzorové riešenie
Ako prvé si treba uvedomiť, že každý prechádzajúci hosť vymení stav dverí s číslami, ktoré delí. Napríklad hosť číslo 7 vymení stav na dverách 7, 14, 21, 28,...,98. Keďže dvere začínajú zamknuté, odomknuté budú práve po nepárnom počte zmien, t.j. budú to len tie dvere, ktoré majú nepárny počet kladných deliteľov.
Teraz sa dá postupovať dvomi spôsobmi, ukážeme si obe možnosti, pričom možnosť číslo 2 je tá "čistejšia".
Prvá možnosť - párovanie
Vezmime si ľubovoľné číslo dverí D a predpokladajme, že a delí D, symbolicky zaznačené ako a \mid D. Potom platí, že máme nejaké iné číslo b (tiež celé), také, že D = a \cdot b. Potom ale nutne platí aj to, že b \mid D. Čiže teraz sme vlastne našli dvojicu deliteľov a teda, keď obaja prejdú, stav sa nezmení (teda aspoň nie vďaka nim, z iných deliteľov sa môže).
Jediná možnosť, ako sa vyhnúť tomu, aby sa pridali dva delitele do počtu, je ak by a = b, lebo potom sa do celkového počtu pridá iba jeden deliteľ. Toto sa môže stať iba ak, pre dané D, vieme nájsť jeho odmocninu. Inak povedané, jediná možnosť ako sa dostať na nepárny počet deliteľov, je to, že číslo D je druhá mocnina iného celého čísla.
Druhá možnosť - prvočíselný rozklad
Vezmime si opäť ľubovoľné číslo D a rozpíšme jeho prvočíselný rozklad (k je počet rôznych prvočísel, ktoré delia D), t.j. D = p_1^{m_1} \cdot p_2^{m_2} \cdot \ldots \cdot p_k^{m_k}. Je známe, že teraz vieme vyjadriť počet deliteľov čísla D ako súčin: (m_1 + 1) \cdot \ldots \cdot (m_k + 1).
Súčin je nepárne číslo práve vtedy, keď je každý činiteľ nepárny. To pre nás znamená, že všetky čísla m_i sú párne. Z toho vieme, že sa dajú zapísať ako m_i = 2 \cdot n_i. Vráťme sa k nášmu prvočíselnému rozkladu D a použime známe pravidlo mocnín a^{b \cdot c} = (a^b)^c. Teda:
D = p_1^{m_1} \cdot p_2^{m_2} \cdot \ldots \cdot p_k^{m_k} \\ D = p_1^{2 \cdot n_1} \cdot p_2^{2 \cdot n_2} \cdot \ldots \cdot p_k^{2 \cdot n_k} \\ D = (p_1^{n_1})^2 \cdot (p_2^{n_2})^2 \cdot \ldots \cdot (p_k^{n_k})^2 \\ D = (p_1^{n_1} \cdot p_2^{n_2} \cdot \ldots \cdot p_k^{n_k})^2
To ale znamená, že číslo D je druhá mocnina a to sme presne chceli.
Odpoveď: Čísla dverí, ktoré sú ráno otvorené, sú druhé mocniny celých čísel do 100, t.j. 1, 4, 9, 16, 25, 36, 49, 64, 81, 100.
Komentár
Väčšina stratených bodov plynula z toho, že ste skočili priamo od nepárneho počtu deliteľov k druhým mocninám, prípadne ste druhé mocniny nikde ani nespomenuli. Môj preferovaný typ riešenia je spôsob číslo 2, ale uznával som aj to, keď ste len spomenuli a rozumne naznačili "párovanie" deliteľov.
10. príklad
Zadanie
Vzorové riešenie
V tomto príklade nemáme až tak uchopiteľné zadanie, ťažko sa nám bude počítať s tabuľkou neznámej veľkosti. Preto je na začiatok asi najlepšie si to vyskúšať pre malé rozmery. Napríklad, pri rozmeroch veľkosti 2 riadky a 3 stĺpce zistíme, že neexistuje ani jeden spôsob, ako splniť zadanie. Podobne si to môžeme všimnúť pre tabuľku 3\times3, alebo vlastne ľubovoľnú tabuľku s tromi, ale napríklad aj piatimi stĺpcami.
Keď si tieto prípady trochu analyzujeme, všimneme si, že keďže v každom riadku musí byť párny počet informácií, tak aj v celej tabuľke bude vždy párny počet informácií. V každom stĺpci je zase nepárny počet informácií, a ak máme v tabuľke nepárne veľa stĺpcov, tak aj celkový počet informácií by musel byť nepárny, čo si protirečí s predošlým tvrdením. Ak je teda v tabuľke nepárny počet stĺpcov, tak sa nedá vyplniť tak, aby bola naraz splnená podmienka pre riadky aj pre stĺpce.
Ďalej potrebujeme zistiť, koľko možností máme v prípade, že je počet stĺpcov párny. V prípade tabuľky 2\times2 sú napríklad iba 2 možnosti – ak si určíme, či v ľavom hornom políčku bude informácia, zvyšok tabuľky sa nám podľa pravidiel určí. Ak by sme ale zvýšili počet riadkov na 3, tak po určení ľavého horného políčka sa nám určí iba prvý riadok. Stále máme možnosť si zvoliť, čo bude v jednom inom políčku, a až vtedy sa nám určí celá tabuľka.
Toto nás môže doviesť k zaujímavému pozorovaniu: Ak v nejakom riadku alebo stĺpci ľubovoľne určíme všetky políčka okrem jedného, tak je jednoznačne určené, či má byť to posledné políčko plné alebo prázdne. Ak ide napríklad o riadok, a vyplnili sme zatiaľ nepárny počet políčok, tak to posledné musíme nutne vyplniť, a vtedy bude riadok vyplnený správne. Rovnako máme práve jednu možnosť aj pre párny počet už vyplnených políčok, a podobne aj pri stĺpcoch.
Zoberme si teda všetky políčka tabuľky okrem posledného riadku a posledného stĺpca, a ľubovoľne ich vyplňme. Teraz nám v každom riadku (okrem posledného) ostáva práve jedno voľné políčko, takže ho vyplníme tak, aby počet informácií v danom riadku sedel. Podobne to urobíme aj pre stĺpce. Takto sme vyplnili celú tabuľku okrem políčka v pravom dolnom rohu, a vieme že sa to dá toľkými spôsobmi, koľkými vieme bez obmedzenia vyplniť tabuľku (a-1)\times(b-1).
Aj políčko v pravom dolnom rohu je jednoznačne určené, máme totiž vyplnený celý zvyšok daného riadku aj daného stĺpca. Tu ale môže nastať problém: čo ak podľa riadku má byť políčko vyplnené ale podľa stĺpca prázdne, alebo naopak? Ak si to vyskúšame pre nejakú konkrétnu tabuľku, zistíme, že sa to nikdy nestáva (stane sa to práve ak je počet stĺpcov nepárny, kde už vieme že je spôsobov 0), skúsme to teda aj dokázať.
Doplňme pravé dolné políčko podľa stĺpca. Dajme tomu, že bol v príslušnom stĺpci nepárny počet vyplnených políčok, a pravé dolné políčko teda necháme prázdne. Keďže sme do nepárneho počtu riadkov dopĺňali informáciu v poslednom stĺpci, tak v časti tabuľky, ktorú sme ľubovoľne vypĺňali, je nepárny počet takých riadkov, ktoré majú vyplnený nepárny počet políčok. Celkovo teda musí byť v tejto časti tabuľky nepárny počet vyplnených políčok.
Teraz sa zaoberáme prípadom, keď je celkový počet stĺpcov párny, a teda v tejto časti tabuľky bez posledného stĺpca bude spolu nepárne veľa stĺpcov. Podobne ako s riadkami, musí byť aj nepárny počet stĺpcov takých, že je v nich nepárne veľa vyplnených políčok aby platilo, že v celej tejto časti tabuľky je spolu nepárny počet vyplnených políčok. Tých zvyšných stĺpcov je teda párne veľa, a práve v nich musíme vyplniť ich posledné políčko. V poslednom riadku celej tabuľky teda vyplníme párny počet políčok, a pravé dolné políčko má ostať aj podľa riadku prázdne.
Ak bol v poslednom stĺpci pôvodne párny počet políčok, musíme pravé dolné políčko vyplniť, a podobne vieme dokázať, že aj posledný riadok bude vyplnený správne.
Ak teda ľubovoľne vyplníme tabuľku bez posledného riadku a stĺpca, máme práve jednu možnosť, ako doplniť zvyšné políčka, aby vyplnenie sedelo. Rozhodovať sa teda môžeme pri (a-1)(b-1) políčkach, pričom pri každom z nich máme nezávisle od seba dve možnosti, ako ho vyplniť. Celkový počet možností je teda 2^{(a-1)(b-1)}.
Pre nepárny počet stĺpcov je teda odpoveď 0, a pre párny počet stĺpcov 2^{(a-1)(b-1)}.
Prémia 1
Zadanie
- Na jednom políčku je vždy najviac jedno zviera.
- Všetky ovce musia byť v jednej oplotenej oblasti. Plot prechádza jedine po stranách štvorčekov a musí byť súvislý.
- Žiaden vlk nemôže byť v oplotenej oblasti.
- Aby sa ovce nepobili, každá môže mať na ôsmich políčkach okolo seba najviac jednu inú ovcu.
Rozostavte zvyšných 60 oviec a postavte plot tak, aby bol obvod plota čo najmenší. Ovcami, ktoré sú už na lúke, nemôžete hýbať.

Vzorové riešenie
Riešenie
Najlepšie riešenie malo obvod lúky 144 hrán. Jeden spôsob opletenia je napríklad takýto (biele ovce sú zo zadania - tie sme neumiestňovali):

Komentár
Viacero z vás si zle prečítalo zadanie a na výslednom plániku ste mali umiestených 60 oviec namiesto 62. V takomto prípade sme za každú chýbajúcu ovcu pripočítali 5 hrán k celkovému obvodu.
Bodovanie
- 145 a menej - 8 bodov
- 146 až 147 - 7 bodov
- 148 až 149 - 6 bodov
- 150 až 151 - 5 bodov
- 152 až 160 - 4 body
- 161 až 170 - 3 body
- 171 až 190 - 2 body
- 191 až 250 - 1 bod
- 251 a viac - 0 bodov