Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

5. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Klausov kompas pozostáva z dotýkajúcich sa krúžkov (znázornené na obrázku). V každom z nich sa nachádza jedno kladné celé číslo, pričom rovnaké čísla sa môžu opakovať. Hrdinovia si vybrali jeden krúžok a spočítali súčet čísel v tých krúžkoch, ktorých sa dotýkal. Zistili, že nech by si vybrali akokoľvek, dostali by ten istý výsledok. Aký najmenší výsledok mohli dostať?

Vzorové riešenie

Opravovali: mati, merlin
1. spôsob

Najprv si označíme čísla v jednotlivých krúžkoch a až g ako na obrázku:

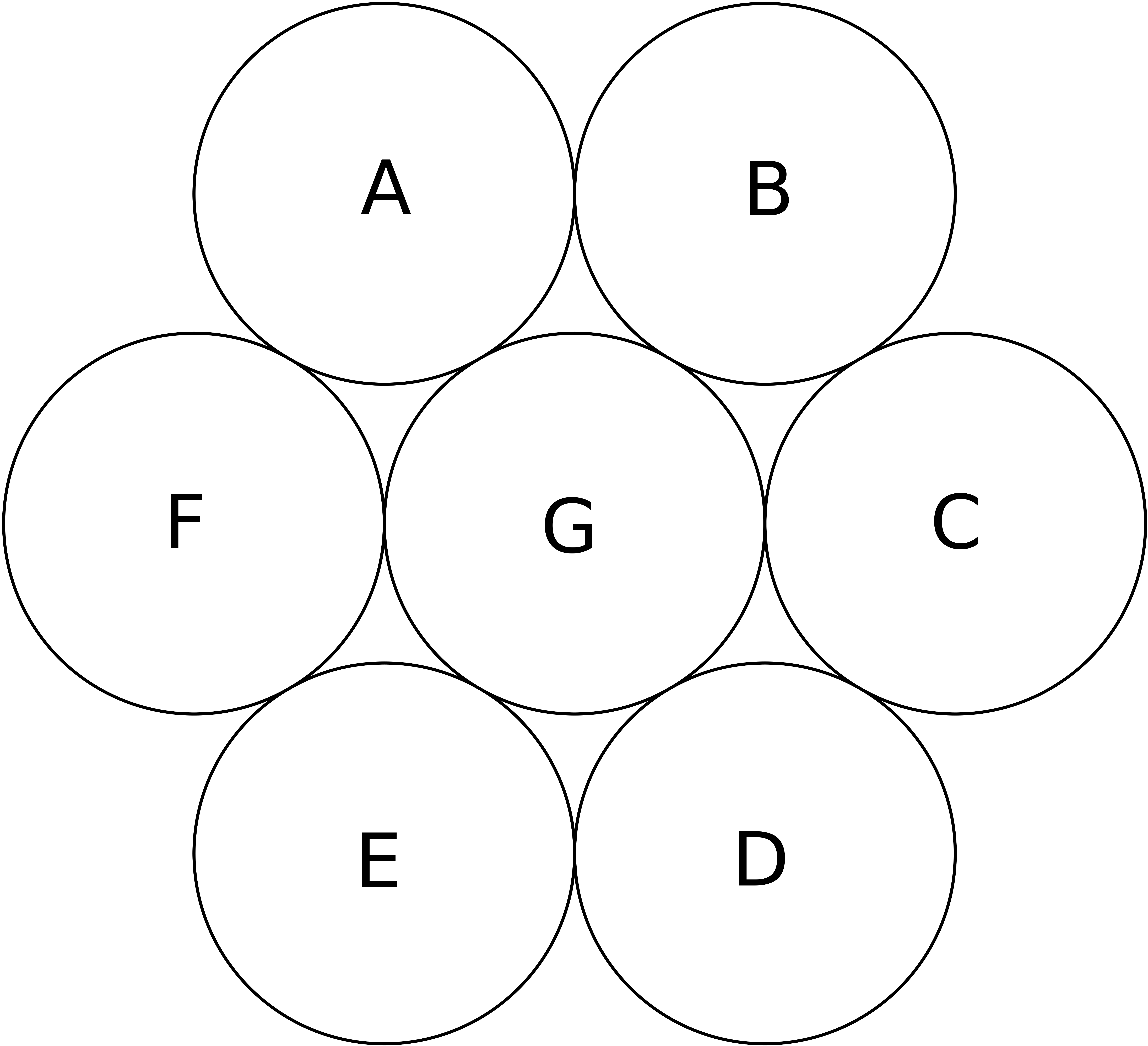
Pozrime sa teraz na súčty susedov krúžkov s číslom a a c. Zo zadania vieme, že tieto súčty musia byť rovnaké a teda dostávame: f+g+b=b+g+d. Po odčítaní g+b z oboch strán, dostávame f = d. Rovnakým postupom vieme dostať aj rovnice f = b, b = d, a = c, c = e a e = a. Keď tieto rovnice spojíme, dostaneme a = b = c a b = d = f.

Teraz sa pozrieme na súčty susedov krúžkov s číslom a a b. Dostávame rovnicu f+g+b = a+g+c. Keďže ako vieme, že a = c a f = b, túto rovnicu si vieme prepísať na 2b + g = 2a + g, teda b = a.

Z toho vyplýva, že všetky čísla na okraji sú rovnaké. Čísla v nich si označme a. Okolo stredného krúžku máme teraz súčet 6a a okolo jedného z okrajových krúžkov máme súčet 2a + g. Teda 6a = 2a + g, z čoho výplíva, že g = 4a.

Keďže máme čísla v každom krúžku vyjadrené pomocou a, tak ak za a dosadíme najmenšie prirodzené číslo, teda 1, tak dostaneme najmenší možný výsledok, ktorý je teda 6.

Výhodou tohto riešenia je, že je všeobecnejšie. Napríklad je pekne vidieť, že výsledok bude násobkom čísla 6, keďže je v tvare 6a. Taktiež keby sa nás niekto pýtal aký je 42. najmenší výsledok, tak nemáme problém za a dosadiť 42 a víde nám 252, pričom pri použití 2. spôsobu nám tieto pekné vlastnosti príkladu pravdepodobne uniknú.

2. spôsob

Pozrime sa na stredný krúžok. Dotýka sa ho 6 krúžkov. Teda najmenší možný súčet, ktorý môžeme dostať je 6, a to vtedy, keď budú všade na okraji najmenšie možné čísla, teda jednotky.

Riešenie, kde je výsledok 6 je napríklad takéto:

Keďže sme si ale dokázali, že výsledok je najmenej 6, toto je najmenšie možné riešenie.

Komentár

Väčšina z vás vyriešila tento príklad bez problémov druhým spôsobom. Veľmi chválime ľudí, ktorí si dali prácu navyše a našli tu odprezentované prvé riešenia. Chýb nebolo veľa, no keď sa našli, väčšinou ste nezdôvodnili, prečo by čísla v okolitých krúžkoch mali byť navzájom rovnaké a potom ste na tom stavali. V prvom riešení si môžete všimnúť ako sa to dalo pekne zdôvodniť. Pri tom druhom je dôležité, že preň nepotrebujeme povedať, že všetky okolité čísla musia byť rovnaké. Stačí nám, že nech sú hocijaké, tak najmenšie prirodzené číslo, ktoré do každého okienka môžeme dať je 1. Aj ak by boli tie čísla rôzne, tak by bol súčet väčší.