Letný tábor 2025 - Milí naši Rieškari, ako je už zvykom, aj tento rok sme si pre Vás pripravili Letný tábor Riešok. Je to desaťdňová akcia počas ktorej sa zabavíte, niečo naučíte a hlavne … Prejsť na článok
×1. príklad
Zadanie
Vzorové riešenie
Keďže nosnosť plte je 70\, \text{kg} tak v jednej plti môže sedieť práve jeden profesor a nič viac, pretože jeho hmotnosť je tiež 70 \, \text{kg}. Ďalej v nej môže sedieť jeden študent, pretože 35\, \text{kg}\lt70\, \text{kg} , alebo práve dvaja študenti, pretože 35\, \text{kg}\cdot2=70\, \text{kg}. Počítač môže byť v plti s práve jedným študentom, pretože
35\, \text{kg}+10\, \text{kg}=45\, \text{kg} a 45\, \text{kg}\lt70\, \text{kg}.
Keďže plť sa nevie hýbať sama, tak potom čo sa profesor s ňou prevezie na druhý breh niekto sa s ňou bude musieť vrátiť, aby sa na druhý breh dokázali dostať aj zvyšní ľudia počítač. Týmto niekým nemôže byť profesor, pretože ak by sa s ňou vrátil on, tak sme práve spravili 2 zbytočné prevezenia.
Z toho vyplýva, že predtým ako sa profesor preplaví na druhý breh, musí už na druhom brehu byť aspoň jeden študent, a zároveň plť musí byť u prvého brehu.
Toto vieme spraviť na najmenej 2 preplávania a to tak, že sa najprv 2 študenti preplavia z prvého na druhý breh a potom sa jeden z nich s plťou vráti. Ďalšie 2 preplávania bude trvať profesorova cesta na druhý breh a následné vrátenia sa študenta, ktorý na druhom brehu zostal, späť na prvý breh.
Takže dostanie každého z profesorov z prvého brehu na druhý trvá najmenej 2+2= 4 prevezenia dokopy teda 4\cdot2=8 prevezení.
Dostať počítač na druhý breh vieme tak, že sa na druhý breh prevezie na jednej plti počítač so študentom a potom sa tento študent vráti.
Na prvom brehu nám potom zostali už iba 2 študenti, ktorí sa vedia dostať na druhý breh na 1 prevezenie.
Dokopy to trvá teda najmenej 8+2+1= 11 prevezení.
Odpoveď: Plť musia previezť cez rieku minimálne 11-krát.
2. príklad
Zadanie
 Poznámka: Obrázok je len ilustračný, dĺžky čiar nemusia zodpovedať reálnym dĺžkam.
Poznámka: Obrázok je len ilustračný, dĺžky čiar nemusia zodpovedať reálnym dĺžkam.
Vzorové riešenie
Riešenie
Voľne si prekreslime obrázok a označme si šesť dĺžok strán písmenami a,b,c,d,e,f.

Pretože všetky útvary sú podľa zadania pravouholníky, vieme s istotou povedať, že každá označená dĺžka sa nachádza v obrázku na práve štyroch miestach - vždy buď pod písmenom, alebo napravo od písmena. Navyše, každé z deviatich "okien" musí byť obdĺžnik (alebo štvorec).
Ako dobre vieme, obsah obĺžnika sa počíta súčinom dĺžok dvoch susedných strán. Preto teraz vieme, že b \cdot e = 4. Keďže všetky dĺžky majú byť celočíselné, máme tri možnosti: b = 1, e = 4 alebo b = 4, e = 1 alebo b = 2, e = 2.
Predpokladajme, že b = 1, e = 4. Ďalej vieme, že a \cdot e = 6, z čoho vyplýva 4a = 6 a následne a = 1,5. To je v rozpore s predpokladom, že všetky dĺžky sú celočíselné. Takže b \neq 1, e \neq 4.
Rovnakým uvažovaním vieme vylúčiť aj možnosť b = 4, e = 1. To by totiž viedlo k záveru, že d = 1,5. Opäť spor, teda b \neq 4, e \neq 1.
Posledná možnosť, ktorá nám zostala, je b = 2, e = 2. Teraz si vieme dopočítať všetky zvyšné dĺžky: Vieme, že platí a \cdot e = 6, z čoho po vydelením e = 2 získame a = 3.
Analogicky zistíme, že c = 6, d = 3, f = 4.
V tejto chvíli máme ale hotovo, lebo poznáme všetkých šesť dĺžok a je jasné, že obvod obrazovky je rovný 2 \cdot (a+b+c) + 2 \cdot (d+e+f). Stačí už len dosadiť: 2 \cdot (3+2+6) + 2 \cdot (3+2+4) = 2 \cdot 11 + 2 \cdot 9 = 40.
Odpoveď: Obvod Michardovej obrazovky je 40.
Komentár
Príklad ste zvládli prevažne dobre. Najčastejšie typy chýb boli: nedokončené vysvetlenie, ako sa od "kríža" dostať ku skutočnému výsledku, zanedbanie niektorej možnosti úplne, alebo to, že ste odovzdali obrázok s výpočtom, za čo sme vám mohli dať iba málo bodov.
3. príklad
Zadanie
- Zvoliť si jedno číslo z dvojice a prirátať k nemu 1.
- Vynásobiť výsledok piatimi.
- Znova prirátať 1.
- Výsledok zdvojnásobiť.
- Odčítať 1.
- Prirátať druhé číslo, ktoré si napísal na papier.
- Prirátať 2.
- Výsledok opäť zdvojnásobiť.
- Odčítať 8.
- Vydeliť dvomi a povedať Neznámemu výsledok.
Vzorové riešenie
Michard si na papier napísal dve čísla od 1 po 9 vrátane. Označme ich A a B.
Potom s nimi spravil týchto 10 operácií:
- Zvolil si jedno číslo z dvojice (číslo A) a prirátal k nemu 1. Dostávame medzivýsledok:
A+1 - Vynásobil výsledok piatimi. Dostávame:
5A+5 - Znova prirátal 1:
5A+6 - Výsledok zdvojnásobil:
10A+12 - Odčítal 1:
10A+11 - Prirátal druhé číslo, ktoré si napísal na papier (číslo B):
10A+B+11 - Prirátal 2:
10A+B+13 - Výsledok opäť zdvojnásobil:
20A+2B+26 - Odčítal 8:
20A+2B+18 - Vydelil dvomi a povedal Neznámemu výsledok:
10A+B+9
Michard povie neznámemu výsledok, ktorý si označíme V=10A+B+9. Keď od obidvoch strán rovnice odčítame 9 dostávame: V−9=10A+B.
Vieme, že obe čísla, A aj B, sú od 1 po 9 vrátane takže 10A bude dvojcifrnéčíslo končiace cifrou 0 a zároveň B bude jednociferné číslo. Teda 10A+B sa bude rovnať dvojcifernému číslu tvoreného ciframi A,B.
Teda keď Neznámy odčítal od výsledku 9 dostal dvojciferné číslo, ktorého prvá cifra (na mieste desiatok) bola A a druhá cifra (na mieste jednotiek) bola B. Takto vedel vždy zistiť aké dve čísla si na začiatku Michard vybral.
4. príklad
Zadanie
Vzorové riešenie
Označme si číslo zo zadania ako ABC, kde jedno písmeno je jedna cifra hesla. Keď škrtneme cifru A, tak dostaneme číslo BC. Keď škrtneme cifru B, tak dostaneme číslo AC. Keď škrtneme cifru C, tak dostaneme číslo AB. Zo zadania vieme, že čísla ABC,\, AB,\, AC a BC sú deliteľné 6.
Číslo je deliteľné 6, ak jeho posledná cifra je deliteľná dvomi a jeho ciferný súčet je deliteľný 3. Čísla ABC,\, AC a BC končia cifrou C a číslo AB končí cifrou B. Preto cifry B a C musia byť párne.
Na to, aby bolo číslo AB deliteľné 3, tak musí mať súčet cifier deliteľný tromi. To isté platí aj o čísle ABC. Vieme, že A + B = číslo deliteľné tromi (označíme si ho k), rovnako ako A + B + C = iné číslo deliteľné tromi (označíme si ho m). Z vyjadrení k,\, m vieme, že m = k + C. Keďže aj k a m sú deliteľné tromi, tak C musí byť tiež deliteľné tromi. Prečo? Lebo ak sčítame číslo deliteľné tromi s číslom nedeliteľným tromi, tak aj výsledné číslo nebude deliteľné tromi. Podobne vieme ukázať, že A aj B musia byť deliteľné tromi.
Vieme, že dvojciferné ani trojciferné číslo nezačína cifrou 0, inak by bolo jednociferné, respektíve dvojciferné. Povedzme, že druhá cifra pôvodného čísla zo zadania je 0, ako napríklad v čísle 306. Vyškrtnutím prvej cifry 3 dostaneme číslo 06, čo zjavne nie je dvojciferné číslo. Preto 0 nemôže byť prvá ani druhá cifra, teda ani A ani B.
Vieme teda, že:
- Všetky cifry musia byť deliteľné tromi.
- Posledné dve cifry (B,\, C) sú párne.
- Prvé dve cifry (A,\, B) nesmú byť 0.
- A musí byť jedno z čísel 3,\, 6,\, 9,
- B musí byť 6,
- C musí byť buď 0 alebo 6.
Pre každú cifru A existuje jedna možnosť pre cifru B a dve možnosti pre cifru C. Preto je 3 \cdot 1 \cdot 2 = 6 možností pre heslo. Týmito možnosťami sú čísla \mathbf{360,\, 366,\, 660,\, 666,\, 960,\, 966}.
5. príklad
Zadanie
Vzorové riešenie
Tento príklad sa dal riešiť postupným skúšaním všetkých možností, ako sa môžeme pohnúť po jednotlivých krokoch. Ak vždy skontrolujeme a vyškrtneme možnosti, ktoré pre nejaké n nesedia, postupne sa dostaneme do bodu, kedy už nevieme žiadnu postupnosť predĺžiť, a teda sme našli najdlhšiu postupnosť pokynov. Existuje ale niekoľko spôsobov, ako si riešenie zjednodušiť.
Dobrou myšlienkou na začiatok je uvedomiť si, že vždy keď urobíme zo stredu krok určitým smerom, nasledujúci krok musíme urobiť opačným smerom, inak spadneme z útesu. Tým sa znova ocitneme v strede, a znova musíme uplatniť to isté pravidlo. Vždy po párnom počte vykonaných krokov (pre ľubovoľné n) teda budeme nutne v strede útesu.
Z toho vieme, že pre možnosť, že si prístroj vyberie n=1, musia byť dvojice pokynov 1. a 2., 3. a 4., 5. a 6., a tak ďalej, vzájomne opačné. Podobne vieme postupovať aj pri iných zvolených n, ako možno vidieť v nasledujúcej tabuľke:
| pre n = | musia byť navzájom opačné | |||||
|---|---|---|---|---|---|---|
| 1 | 1. a 2. | 3. a 4. | 5. a 6. | 7. a 8. | 9. a 10. | 11. a 12. |
| 2 | 2. a 4. | 6. a 8. | 10. a 12. | |||
| 3 | 3. a 6. | 9. a 12. | ||||
| 4 | 4. a 8. | 12. a 16. | ||||
| 5 | 5. a 10. | |||||
| 6 | 6. a 12. | |||||
Označme si pokyn “krok dopredu” P a pokyn “krok dozadu” Z. Nemusíme ale rozoberať aj možnosti, keď je prvý pokyn P aj keď je Z. Keď si vyberieme hociktorú z týchto možností a podľa toho napíšeme postupnosť, analogickú postupnosť vieme napísať aj s opačným začiatočným pokynom, a to tak, že iba všetky pokyny otočíme. Tiež budú platiť všetky argumenty, ktorými sme iné postupnosti vylúčili, keď v nich vymeníme smery. Bez toho aby to ovplyvnilo riešenie, si teda zvoľme, že začneme pokynom P.
Aký môže byť vtedy druhý pokyn? Ako už vieme, keby sme zadali ako ďalší pokyn P, spadne prístroj z útesu. Musíme preto zadať pokyn Z .PZ
Teraz sa pozrieme na štvrtý pokyn. Ak n=2, tak prvý vykonaný pokyn je Z. Z toho vyplýva, že druhý vykonaný pokyn, štvrtý celkovo, musí byť P.PZ?P.
Z tabuľky vidíme, že kvôli možnosti n=1 musia byť 3. a 4. pokyn navzájom opačné. Teda tretí pokyn musí byť Z.PZZP
Vieme, že kvôli n=3 musia byť aj 3. a 6. pokyn opačné, teda 6. pokyn bude P.
PZZP?P
Aký môže byť piaty pokyn? Kvôli n=1 musí byť opačný ako 6. pokyn, teda Z.
PZZPZP
Ôsmy pokyn musí byť kvôli n=4 opačný ako štvrtý, teda v našom prípade Z.
PZZPZP?Z
Siedmy pokyn potom musí byť kvôli n=1 opačný ako ôsmy, teda P.
PZZPZPPZ
Desiaty pokyn musí byť kvôli n=5 opačný ako piaty, teda P.
PZZPZPPZ?P
Deviaty pokyn vtedy musí byť kvôli n=1 opačný ako desiaty, teda Z
PZZPZPPZZP
Dvanásty pokyn kvôli n=6 musí byť opačný ako šiesty, teda Z. Aby ale prístroj nespadol ani ak si vyberie číslo n=3, musí byť dvanásty pokyn opačný ako deviaty, teda P. Určite nemôže byť pokyn P aj Z naraz, vidíme teda, že pri 12. pokyne môže prístroj spadnúť tak či tak.
Zostal ešte jedenásty pokyn. Ten vieme zadať aj ako P aj ako Z s tým, že prístroj určite nespadne nech si vyberie akékoľvek n.
Teraz je dôležité nakoniec overiť, že naša postupnosť je naozaj taká, že prístroj nespadne nech si zvolí ľubovoľné n.
- Ak n=1, tak sa vykonajú pokyny PZZPZPPZZP a nakoniec Z alebo P, prístroj ani v jednom prípade nespadol.
- Ak n=2, vykonajú sa pokyny ZPPZP, vidíme, že ani teraz stroj nespadne.
- Ak n=3, vykonajú sa pokyny ZPZ, teda ani tu prístroj nespadne.
- Ak n=4, vykonajú sa pokyny PZ, prístroj nespadne.
- Ak n=5, vykonajú sa pokyny ZP, prístroj nespadne
- Ak je n viac ako 6, vykoná sa vždy najviac jeden pokyn, tieto čísla majú totiž všetky okrem prvého násobku väčšie ako 11, čiže nie sú v našej postupnosti. Keďže urobíme iba jeden alebo žiaden krok, prístroj z útesu určite nespadne.
Dokázali sme teda, že neexistuje vyhovujúca postupnosť dlhšia ako 11 pokynov, a našli sme niekoľko správnych postupností práve tejto dĺžky, napríklad: PZZPZPPZZPP
Kľúčové v celom postupe je ukázať, že pri 12. pokyne sa už naša postupnosť určite pokazí, a že existuje nejaká funkčná dĺžky 11. Týmto máme zaručené, že odpoveď na úlohu je 11. Preto ako dôkaz úplne stačilo nasledovné:
Druhé riešenie
Vytvoríme podobnú tabuľku ako sa nachádza v prvom riešení, alebo slovne popíšeme, prečo párne pokyny v postupnostiach pre všetky n musia byť opakmi predošlých pokynov.
Vidíme, že ak je v postupnosti 12. pokyn, tak 9. pokyn, musí byť opačný ako 12. pokyn (kvôli n=3), a 12. pokyn musí byť opačný ako 10 (kvôli n=2). Z toho vyplýva, že 9. pokyn musí byť rovnaký ako 10. Avšak vieme, že pri takejto postupnosti by Michard spadol z útesu, pretože 9. a 10. pokyn nemôže byť rovnaký kvôli n=1.
Tým pádom sme dokázali, že správna postupnosť 12 a viac pokynov určite nemôže existovať. Teraz ak nájdeme postupnosť pre 11 ktorá platí pre všetky n, tak sme dokázali, že najdlhšia možná postupnosť má 11 pokynov. Takáto postupnosť je napríklad: PZZPZPPZZPP
Komentár
V príklade sa vyskytli dva kroky, ktoré mnohí riešitelia zabudli spomenúť, aj keď došli k správnemu výsledku. Prvým bol postreh, že to či začneme pokynom dopredu alebo dozadu maximálny počet pokynov v postupnosti neovplyvní. Druhým dôležitým krokom bola skúška správnosti, teda či postupnosť pokynov ktorú sme našli bola naozaj taká, že prístroj určite nespadne. Dala sa robiť po každom kroku, stačilo ju ale spomenúť aj na konci riešenia. Tieto dva princípy, symetrickosť a skúška správnosti, sú dôležitou časťou mnohých riešení, treba na ne v podobných príkladoch vždy myslieť.
6. príklad
Zadanie
- Najväčší spoločný deliteľ Michardovho čísla a Vikielovho čísla je 15.
- Najväčší spoločný deliteľ Vikielovho čísla a Eninho čísla je 6.
- Súčin Vikielovho čísla a Eninho čísla je 1 800.
- Najmenší spoločný násobok Michardovho čísla a Vikielovho čísla je 3 150.
Vzorové riešenie
Označme najmenší spoločný násobok čísel A,\, B ako \text{NSN}(A,B) a ich najväčší spoločný deliteľ \text{NSD}(A,B). Keď \text{NSD}(A,B) = C, tak vieme povedať že číslo C delí čísla A,B, nakoľko C je ich spoločným deliteľom. Michardovo číslo označíme M, Vikielovo číslo označíme V a Enino číslo označíme E. Dostávame:
\begin{aligned} M &= 3\cdot 5\cdot m\\ V &= 2\cdot 3\cdot 5 \cdot v\\ E &= 2\cdot 3\cdot e \end{aligned}
Keď sa pozrieme na podmienku E\cdot V = 1800, tak zistíme, že musí platiť e \cdot v = 10 = 2\cdot 5. Pozrime sa na to, kam môže táto dvojka a päťka ísť.
Ak by dvojka išla do v, tak V je aspoň 60. To je však problém, lebo 60 nedelí 3150, teda neplatí podmienka pre \text{NSN}(M,V). Z toho vieme, že dvojka musí patriť do e.
Ak by päťka išla do e, tak E je aspoň 30. Potom by však \text{NSD}(E,V) bolo aspoň 30, keďže E,V sú deliteľné 30. Preto 5 patrí do v a teda vieme určiť čísla E,V:
\begin{aligned} M &= 3\cdot 5\cdot m\\ V &= 2\cdot 3\cdot 5 \cdot 5 = 150\\ E &= 2\cdot 2 \cdot 3 = 12 \end{aligned}
Žiadne ďalšie možnosti na E,V nemáme, lebo sme ich určili jednoznačne a ani na M, pretože M môže obsahovať iba prvočísla 2,3,5,7 aby bol \text(M,V) rovný 3150, ale pre každé z týchto prvočísel sme povedali koľko krát môžu byť v M.
Už len zostáva zistiť M. Z podmienky \text{NSD}(M,V) = 15 vyplíva že 5 delí M práve raz, teda nemôže sa stať, že 25 delí M, lebo potom by bol väčší spoločný deliteľ. Z rovnakého dôvodu 2 nedelí M. Zároveň z podmienky \text{NSN}(M,V) = \text{NSN}(M,150) = 3150 = 2\cdot 7 \cdot 9 \cdot 25 máme, že 7,9 musia deliť M, keďže nedelia 150. Naše čísla teda sú:
\begin{aligned} M &= 3 \cdot 3 \cdot 5 \cdot 7 = 315\\ V &= 2 \cdot 3 \cdot 5 \cdot 5 = 150\\ E &= 2 \cdot 2 \cdot 3 = 12 \end{aligned}
Žiadne ďalšie riešenia nie sú, lebo M môže z podmienky o najmenšom spoločnom násobku obsahovať iba prvočísla 2,3,5,7, ale pre každé sme určili, koľko krát musí byť v M. E,V sú určené jednoznačne, teda sme prišli k jedinému možnému výsledku. Dosadením čísel do podmienok si môžte overiť, že toto riešenie naozaj funguje.
Komentár
Veľa z vás malo problém s tým ako sa používa najmenší spoločný násobok alebo najväčší spoločný deliteľ. Vieme že v súčasnej situácií nie každá škola ide podľa rovnakých osnov, preto ak máte akékoľvek nejasnosti k zadaniam, tak nám môžte napísať na zadania@riesky.sk alebo do komentára k príkladu priamo na stránke.
Taktiež si treba dať pozor na to, aby ste zdôvodnili to čo naozaj treba. Nezáleží na tom, koľko budete rozoberať možností, keď potom preskočíte tri kroky a nič k nim nenapíšete.
7. príklad
Zadanie
Vzorové riešenie
Nazačiatok, obvodovou vzdialenosťou nazvime množstvo krokov, ktoré musíme spraviť po stranách nášho 80-uholníka, aby sme sa dostali z bodu X do bodu Y. Potom priamou vzdialenosťou nazvime najkratšiu dĺžku, ktorú musíme prekonať pri pohybe z bodu X do bodu Y, ak môžeme ísť aj mimo strán 80 - uholníka. Ide o dĺžku čiary spájajúcu tieto 2 body.
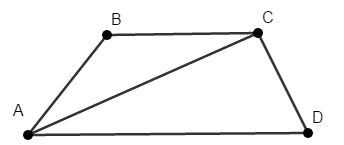
Príklad sa skladal z dvoch dôležitých krokov. Najprv bolo treba ukázať, že nech si vyberieme body nášho 80-uholníka, do nášho 27-uholníka ľubovoľne, tak určite nájdeme trojicu bodov, ktorých obvodová vzdialenosť bude 1, alebo 2\, \text{cm}. Napríklad by to mohli byť body A,C s obvodovou vzdialenosťou 2\, \text{cm} alebo C,D s obvodovou vzdialenosťou 1\, \text{cm}.
V druhej časti bolo treba ukázať, že ak si z nášho 80-uholníka vyberieme body, ktorých obvodová vzdialenosť je 2\, \text{cm}, tak ich skutočná vzdialenosť musí byť menšia.
- Keďže 80-uholník má 80 strán, tak poďme zistiť, koľko strán s obvodovou vzdialenosťou 3 tam zmestíme. Keď predelíme 80 3-kou aby sme dostali, koľko takýchto stán tam vieme zmestiť, tak dostaneme 26,\overline{6} \, (\frac{80} {3}=26,\overline{6}). Z toho vyplíva, že tam maximálne zmestíme 26 strán s obvodovou dlžkou 3 a viac. Potom ale posledná musí byť kratšia.
- Teraz vieme, že ak si zvolíme body do 27 - uholníka ľubovoľne, tak aspoň jedna zo strán bude mať obvodovú vzdialenosť menšiu ako 3\, \text{cm}.
- Ak má táto strana obvodovú vzdialenosť 1\, \text{cm}, tak to je ľahké, lebo priama vzdialenosť sa s obvodovou zhoduje a je tiež 1\, \text{cm}, čo je menej ako 2.
Ak má táto strana obvodovú vzdialenosť 2\, \text{cm}, tak je jasné, že body A,\, B a C tvoria trojuholník. Jediná iná možnosť je, že by ležali na jednej priamke no vtedy by nemohli byť vrcholmi pravidelného 80-uholníka. Potom však úsečka AC musí mať menej ako 2\, \text{cm}, tí ktorí poznáte trojuholníkovú nerovnosť určite viete, že súčet ľubovoľných 2 strán trojuholníka musí byť dlhší ako tá tretia: |AB| + |BC| = 1\, \text{cm} + 1\, \text{cm} = 2 \text{cm} > |AC|
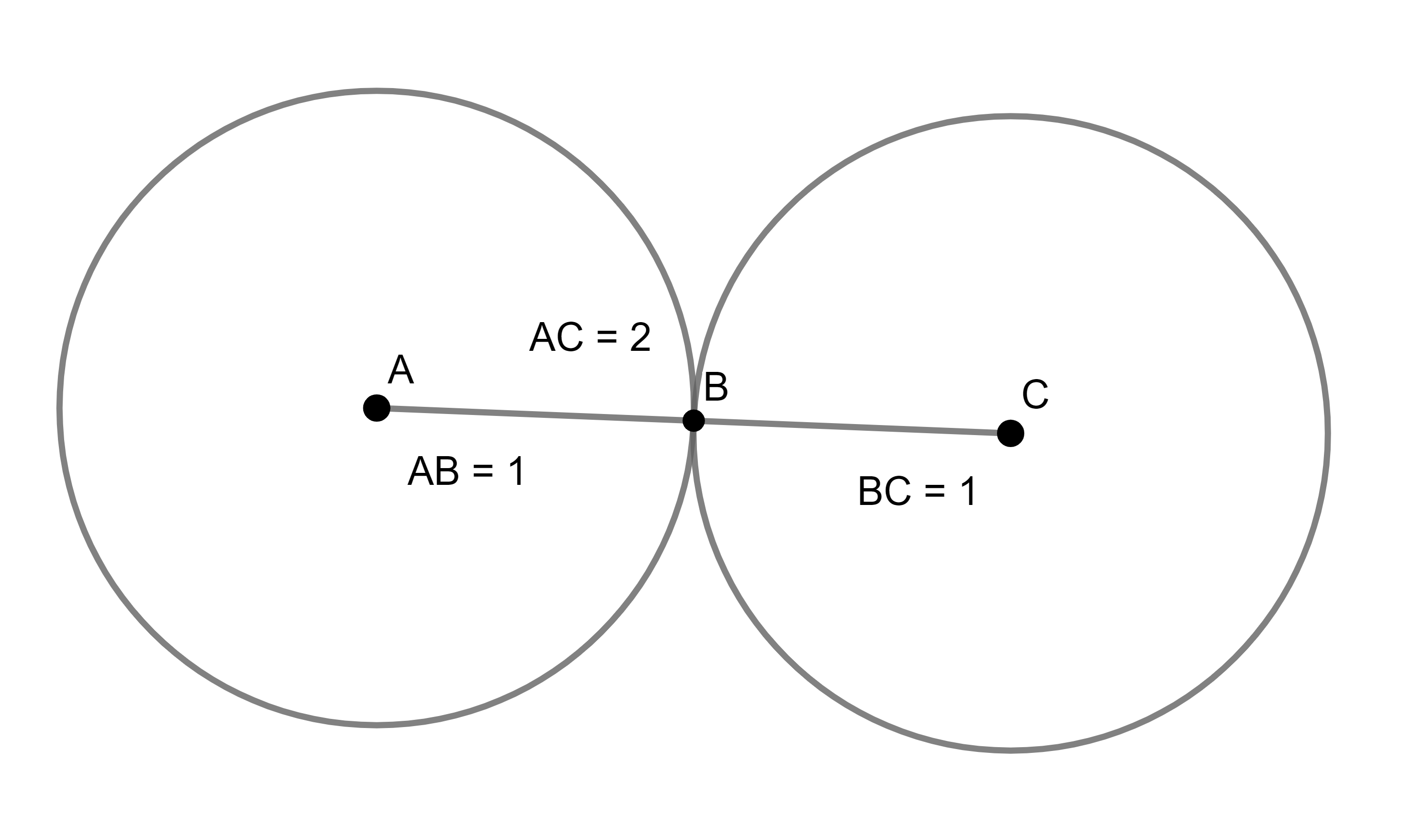
A teda priama dĺžka AC je naozaj kratšia ako 2\, \text{cm} i keď obvodová dĺžka je 2\, \text{cm}. Ak trojuholníkovú nerovnosť nepoznáte, tak sa neváhajte pohrať s pravítkom a ceruzkou, skúste si nakresliť trojuholník so stranami dlhými 3\, \text{cm},\, 5\, \text{cm},\, 9\, \text{cm} a potom 1\, \text{cm},\, 1\, \text{cm},\, 2\, \text{cm}, či 2\, \text{cm},\, 2\, \text{cm},\, 3\, \text{cm}. Skúste aj iné, uvidíte, ktoré sa vám nakresliť podarí, ktoré nie. No vo všeobecnosti platí, že keď je súčet 2 kratších strán menší ako najdlhšia strana, tak nie sú dosť dlhé na to, aby na seba “dočiahli“. Môžete to vidieť aj na obrázkoch.
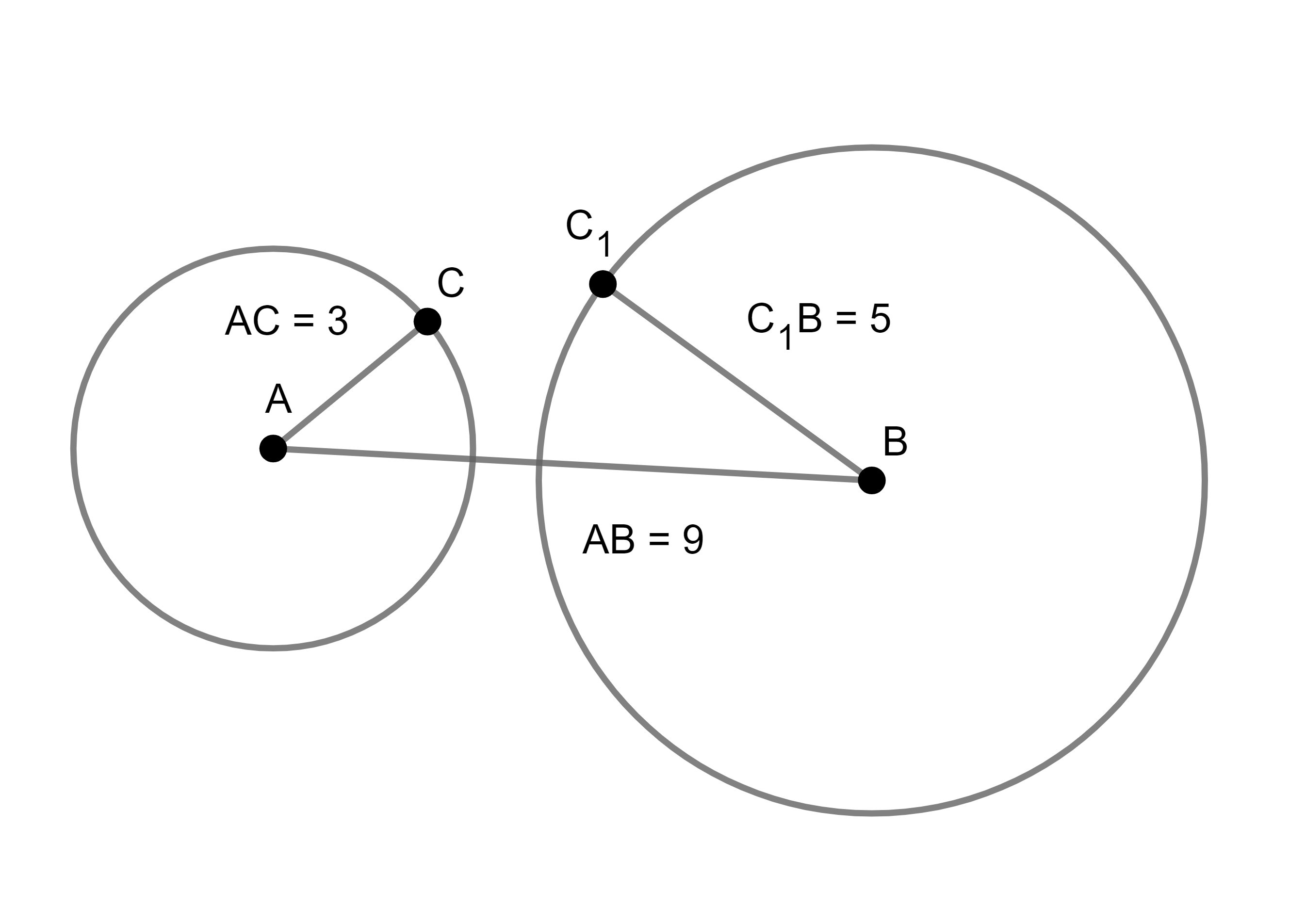
Nech si teda zvolíme rozloženie vrcholov nášho 27–uholníka v 80–uholníku ľubovoľne, tak aspoň 1 strana bude mať dĺžku menšiu ako 2\, \text{cm}.
Komentár
Väčšina z vás príklad zvládla veľmi pekne. Chyby najčastejšie vyplývali z toho, že ste buď vôbec, alebo nedostatočne zdôvodnili, prečo ak je obvodová vzdialenosť dvoch bodov 2\, \text{cm}, tak ich skutočná vzdialenosť musí byť menšia. Poprípade niektorí nezdôvodnili, prečo aspoň 1 zo strán 27–uholníka pri ľubovoľnom výbere vrcholov, musí mať obvodovú vzdialenosť menšiu ako 2\, \text{cm}.
8. príklad
Zadanie
- Dokážte, že štvoruholník OPQR je rovnobežníkom.
- Dokážte, že \measuredangle ABC = \measuredangle PQR.
Vzorové riešenie
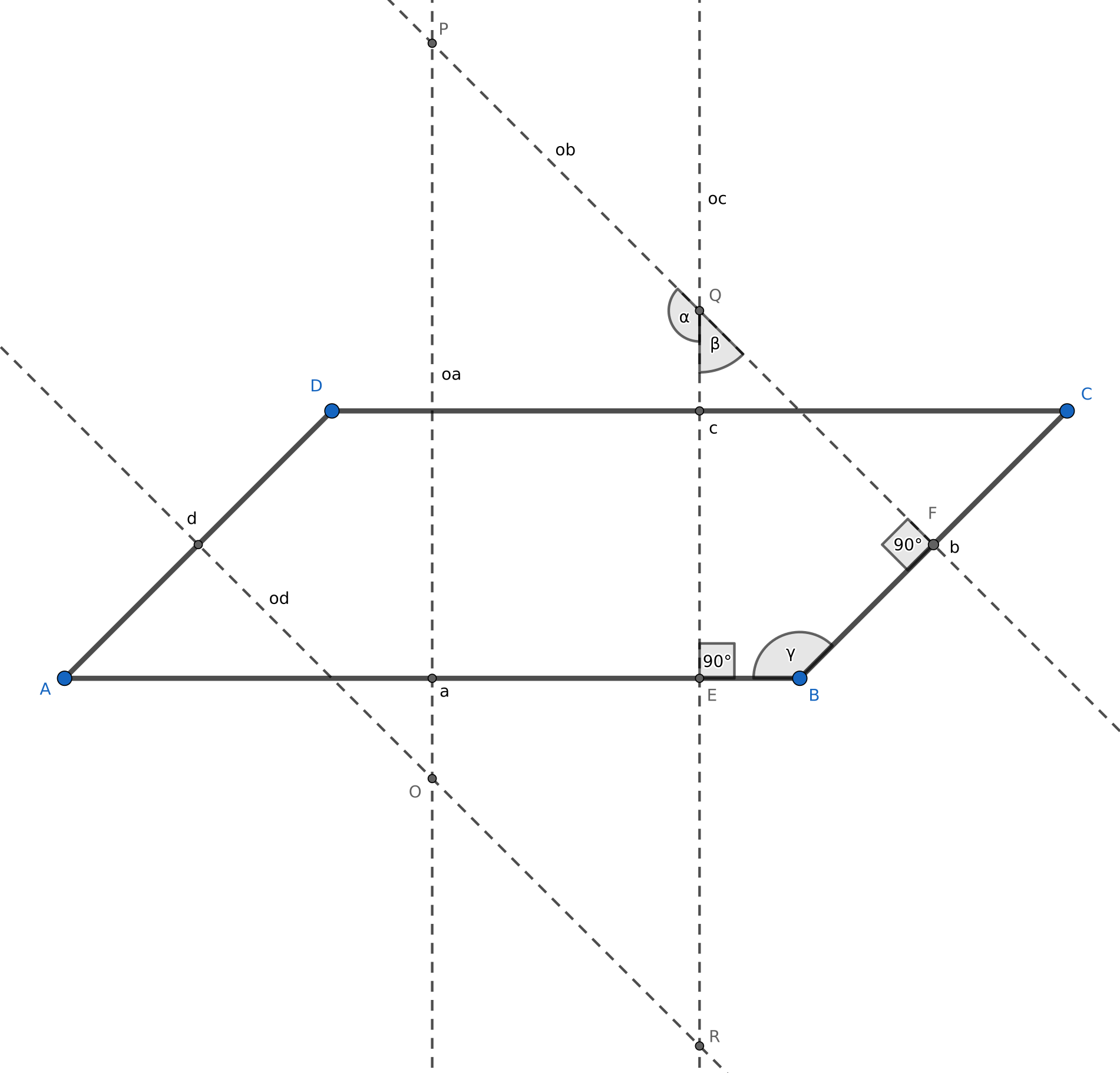
a)
Na obrázku vidíme rovnobežník ABCD. Stred kružnice opísanej trojuholníku je priesečníkom osí strán trojuholníka, avšak stačia nám len dve. V obrázku si označíme osi strán tohto rovnobežníka. Pomocou oa a od zistíme bod O ktorý leží v ich priesečníku, pomocou oa a ob zistíme bod P, ob a oc určuje bod Q a v priesečníku oc a od je bod R. Keďže os strany je kolmica na danú stranu, osi strán budú tiež na seba rovnobežné (kolmice na rovnobežky sú tiež rovnobežné). Tým pádom má vzniknutý útvar OPQR dve a dve protiľahlé strany rovnobežné, čiže to je rovnobežník.
b)
Vo vzniknutom obrázku si vyznačíme bod E, ktorý je priesečníkom oc a úsečky AB, bod F je priesečníkom ob a úsečky BC. Potom si vyznačíme uhly \alpha = \measuredangle PQR, \beta = \measuredangle RQF a ako posledné \gamma = \measuredangle ABC.
Môžme si všimnúť, že \alpha = 180 - \beta, keďže sú to susedné uhly. O uhle \gamma vieme, že je vnútorným uhlom štvoruholníka EBQF. Tiež vieme, že úsečka EQ je kolmá na EB a FQ je kolmá na BF. Keďže vieme, že súčet vnútorných uhlov štvoruholníka je 360\degree, tak odčítame tieto dva pravé uhly a ostane nám, 180 = \beta + \gamma. To vieme upraviť na \gamma = 180 - \beta a keďže \alpha = 180 - \beta vidíme, že \measuredangle OPQ = \measuredangle ABC.
Komentár:
Príklad vás riešilo pomenej, no za to ste ho väčšina veľmi pekne zvládli. Hlavným nedostatkom bývali chyby vo vysvetlení, prípadne niektoré časti neboli vysvetlené vôbec, čo sa odzrkadlilo aj na bodovaní.
9. príklad
Zadanie
Vzorové riešenie
Pôvodná postupnosť zo zadania vyzerá nasledovne:
Vieme, že členy postupnosti, ktoré vzniknú sčítaním dvoch predchádzajúcich členov a tie ktoré vzniknú odčítaním dvoch predchádzajúcich členov sa striedajú. Z toho vyplýva, že každý člen postupnosti, ktorý sa nachádza na nepárnej pozícií, vznikol sčítaním dvoch predchádzajúcich členov, a každý člen postupnosti, ktorý sa nachádza na párnej pozícií, vznikol odčítaním dvoch predchádzajúcich členov. Toto samozrejme neplatí pre prvé dva členy postupnosti, keďže tie pred sebou nemajú dva iné členy.
Označme si potom člen postupnosti na nejakej nepárnej pozícii (2k+1) ako x. Člen, ktorý bude nasledovať hneď po ňom si označme ako y. Potom vieme, že nasledujúci člen je rovný výrazu x+y, keďže má ako člen na nepárnej pozícií tvar súčtu dvoch predchádzajúcich členov. Ďalší člen je zas rovný výrazu (x+y)-y=x, keďže je ako člen na párnej pozícií rozdielom dvoch predchádzajúcich členov. A nakoniec (2k+5)-ty člen je rovný výrazu (x+y)+x=2x+y, keďže je ako člen na nepárnej pozícií súčtom dvoch predchádzajúcich členov.
Čiže týchto 5 členov nasleduje za sebou takto:
Po vyškrtnutí každého druhého člena nám zostanú len členy na nepárnych pozíciach. To sú v našom prípade x, (x+y), (2x+y). Vidíme, že keď sčítame prvý z nich s druhým, tak dostaneme tretí člen, lebo x+(x+y)=(2x+y). Zistili sme teda, že tretí člen je naozaj súčtom dvoch predchádzajúcich členov. Teda podmienka zo zadania, že po vyškrtnutí všetkých členov na párnych pozíciach dostaneme novú postupnosť, v ktorej bude každý člen súčtom dvoch predchádzajúcich členov, platí pre túto päticu členov od (2k+1)-vého členu po (2k+5)-ty člen.
Za k si pri našich piatich členoch vieme zvoliť ľubovoľné nezáporné celé číslo, a tak platí podmienka zo zadania pre všetky pätice členov v pôvodnej postupnosti a teda i pre celú postupnosť. Tým sme i ukončili dôkaz tejto úlohy.
10. príklad
Zadanie
Vzorové riešenie
Zo zadania knižnica môže byť v ľubovoľnom bode štvorca alebo na obvode štvorca ABCD, tak nech je v bode K. Veďme rovnobežky so stranami štvorca cez bod K a priesečníky so stranami označíme E,\, F,\, G,\, H v poradí. Vzniknuté štvoruholníky AEKH,\, EBFK,\, KFCG,\, HKGD budú obdĺžnikmi, keďže strany štvorca sú na seba kolmé a rovnako aj na priamky precházdajúce cez bod K.
Môžeme si určiť dĺžku strany štvorca 1. Pre ľubovoľnú inú stranu, by sme všetky dĺžky prenásobili jej dĺžkou a počítali rovnako. Takto si zjednodušíme prácu. Ďalej nech obdĺžnik AEKH má dĺžky strán x a y. Keďže ABCD je štvorec, tak vieme vyjadriť všetky dĺžky strán zvyšných obdĺžnikov s vrcholom K, tak ako vidno na obrázku.
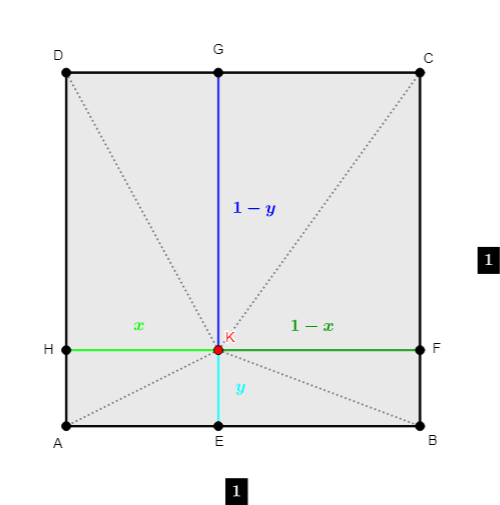
x^2 + y^2 + (1-x)^2 + y^2 + x^2 + (1-y)^2 + (1-x)^2 + (1-y)^2 = \\ = 4 \cdot x^2 + 4 \cdot y^2 - 4 \cdot x - 4 \cdot y + 4 = \\ = 4 \cdot (x^2 + y^2 - x - y + 1) = \\ = 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1)
Na to, aby v tomto bode mohla byť knižnica, musí platiť, že hodnota výrazu 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1) bude najväčšia možná, teda musíme určiť pre aké x a y má výraz najväčšiu možnú hodnotu. Keďže x a y sú od seba nezávislé, môžeme im určiť najväčšiu možnú hodnotu samostatne.
Na začiatku sme si určili stranu štvorca 1 a bod K vnútri alebo na obvode štvorca. Pre dĺžku x bude platiť 0 \leq x \leq 1, teda výraz x-1 je menší alebo rovný 0. Súčin kladného a záporného čísla je záporný. Z toho vyplýva, že hodnota x \cdot (x-1) nemôže byť kladná, lebo platí 0 \leq x \leq 1 a -1 \leq x \leq 0, ale môže byť 0. Preto najväčšia hodnota, ktorú môže nadobúdať výraz x \cdot (x-1) je 0. To nastáva v prípadoch, keď sa buď x = 0 alebo x-1 = 0. Konečne dostávame, že x \in \lbrace 0,1 \rbrace, čo je práve vtedy, keď bod K leží na priamke AD alebo BC.
Podobným spôsobom sa vieme dopracovať k y \in \lbrace 0, 1 \rbrace, teda že bod K leží na primake AB alebo CD.
Ako sme spomínali, aby hodnota 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1) bola čo najväčšia, tak musí byť každá časť výrazu, čo najväčšia, teda x a y musia byť rovné 0 alebo 1.
To nám dáva štyri možnosti kde môže byť knižnica:
- x=0 a y=0, čo je prienik AB a AD \to v bode A
- x=0 a y=1, čo je prienik AB a BC \to v bode B
- x=1 a y=0, čo je prienik CD a AD \to v bode D
- x=1 a y=1, čo je prienik CD a BC \to v bode C
Odpoveď: Najväčšia hodnota bude vo vrcholoch štvorca, teda knižnica sa nachádza v niektorom z nich.
Prémia 1
Zadanie

 Poznámka: Dve pentominá považujeme za rovnaké, ak z jedného dokážeme získať druhé pomocou otáčania a preklápania.
Poznámka: Dve pentominá považujeme za rovnaké, ak z jedného dokážeme získať druhé pomocou otáčania a preklápania.
Vzorové riešenie
Cieľom úlohy bolo dvoma spôsobmi pokryť mriežku 6×10 dvanástimi pentominami tak, aby po prekrytí oboch rozložení zostalo čo najmenej hrán, ktoré nie sú na hranici medzi dvoma pentominami (v rovnakej vrstve). To by mohlo vyzerať nejako takto:

V prvom obrázku je jedno rozloženie, v druhom druhé, a v treťom sú obe prekryté.
Teraz už len stačí zrátať, koľko hrán mriežky nebolo zvýraznených. V tomto prípade je to 12, čo je aj najlepšie riešenie, ktoré sa vám podarilo nájsť.
Bodovanie
Cieľom bolo mať takýchto nevyznačených hrán čo najmenej, teda čím viac ste ich mali, tým menej bodov ste dostali. Bodovali sme podľa nasledujúcej škály:
- 12 hrán - 8 bodov
- 13 až 15 hrán - 7 bodov
- 16 až 18 hrán - 6 bodov
- 19 až 21 hrán - 5 bodov
- 22 až 23 hrán - 4 body
- 24 hrán - 3 body
- 25 až 26 hrán - 2 body
- 27 až 36 hrán - 1 bod
- 37 a viac - 0 bodov
Komentár
Viacerí z vás celkom nepochopili, čo bolo cieľom úlohy. Potom ste často robili napríklad to, že v oboch rozloženiach ste na rovnaké miesta dali rovnaké pentominá, čo sa zjavne neoplatí (ľubovoľné iné rozmiestnenie pokrývajúce rovnaké políčka je lepšie). Vo väčšine prípadov ste aj napriek nepochopenému zadaniu splnili všetky podmienky zo zadania. Z takýchto riešení sme teda mohli zrátať váš výsledok, aj keď ste sa snažili o niečo iné. Pokiaľ ste však v niektorom z rozložení mali pentominá rovnakého tvaru ktoré susedili, nemohli sme vám dať žiadne body.