Odporúčaný článok

Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok

×

7. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Na mape bol zobrazený pravidelný 80-uholník s dĺžkou strany 1, kde každý vrchol označoval miesto, kde existuje hra. Ukážte, že keď si naši traja hrdinovia spomedzi vrcholov tohto 80-uholníka vyberú 27 vrcholov a pospájajú ich do 27-uholníka, tak aspoň jedna strana tohto 27-uholníka bude kratšia ako 2.

Vzorové riešenie

Opravovali: Livka, duško, mati

Nazačiatok, obvodovou vzdialenosťou nazvime množstvo krokov, ktoré musíme spraviť po stranách nášho 80-uholníka, aby sme sa dostali z bodu X do bodu Y. Potom priamou vzdialenosťou nazvime najkratšiu dĺžku, ktorú musíme prekonať pri pohybe z bodu X do bodu Y, ak môžeme ísť aj mimo strán 80 - uholníka. Ide o dĺžku čiary spájajúcu tieto 2 body.

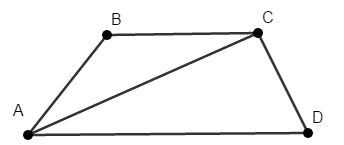
Príklad sa skladal z dvoch dôležitých krokov. Najprv bolo treba ukázať, že nech si vyberieme body nášho 80-uholníka, do nášho 27-uholníka ľubovoľne, tak určite nájdeme trojicu bodov, ktorých obvodová vzdialenosť bude 1, alebo 2\, \text{cm}. Napríklad by to mohli byť body A,C s obvodovou vzdialenosťou 2\, \text{cm} alebo C,D s obvodovou vzdialenosťou 1\, \text{cm}.

V druhej časti bolo treba ukázať, že ak si z nášho 80-uholníka vyberieme body, ktorých obvodová vzdialenosť je 2\, \text{cm}, tak ich skutočná vzdialenosť musí byť menšia.

  1. Keďže 80-uholník má 80 strán, tak poďme zistiť, koľko strán s obvodovou vzdialenosťou 3 tam zmestíme. Keď predelíme 80 3-kou aby sme dostali, koľko takýchto stán tam vieme zmestiť, tak dostaneme 26,\overline{6} \, (\frac{80} {3}=26,\overline{6}). Z toho vyplíva, že tam maximálne zmestíme 26 strán s obvodovou dlžkou 3 a viac. Potom ale posledná musí byť kratšia.

  2. Teraz vieme, že ak si zvolíme body do 27 - uholníka ľubovoľne, tak aspoň jedna zo strán bude mať obvodovú vzdialenosť menšiu ako 3\, \text{cm}.

    • Ak má táto strana obvodovú vzdialenosť 1\, \text{cm}, tak to je ľahké, lebo priama vzdialenosť sa s obvodovou zhoduje a je tiež 1\, \text{cm}, čo je menej ako 2.

    • Ak má táto strana obvodovú vzdialenosť 2\, \text{cm}, tak je jasné, že body A,\, B a C tvoria trojuholník. Jediná iná možnosť je, že by ležali na jednej priamke no vtedy by nemohli byť vrcholmi pravidelného 80-uholníka. Potom však úsečka AC musí mať menej ako 2\, \text{cm}, tí ktorí poznáte trojuholníkovú nerovnosť určite viete, že súčet ľubovoľných 2 strán trojuholníka musí byť dlhší ako tá tretia: |AB| + |BC| = 1\, \text{cm} + 1\, \text{cm} = 2 \text{cm} > |AC|

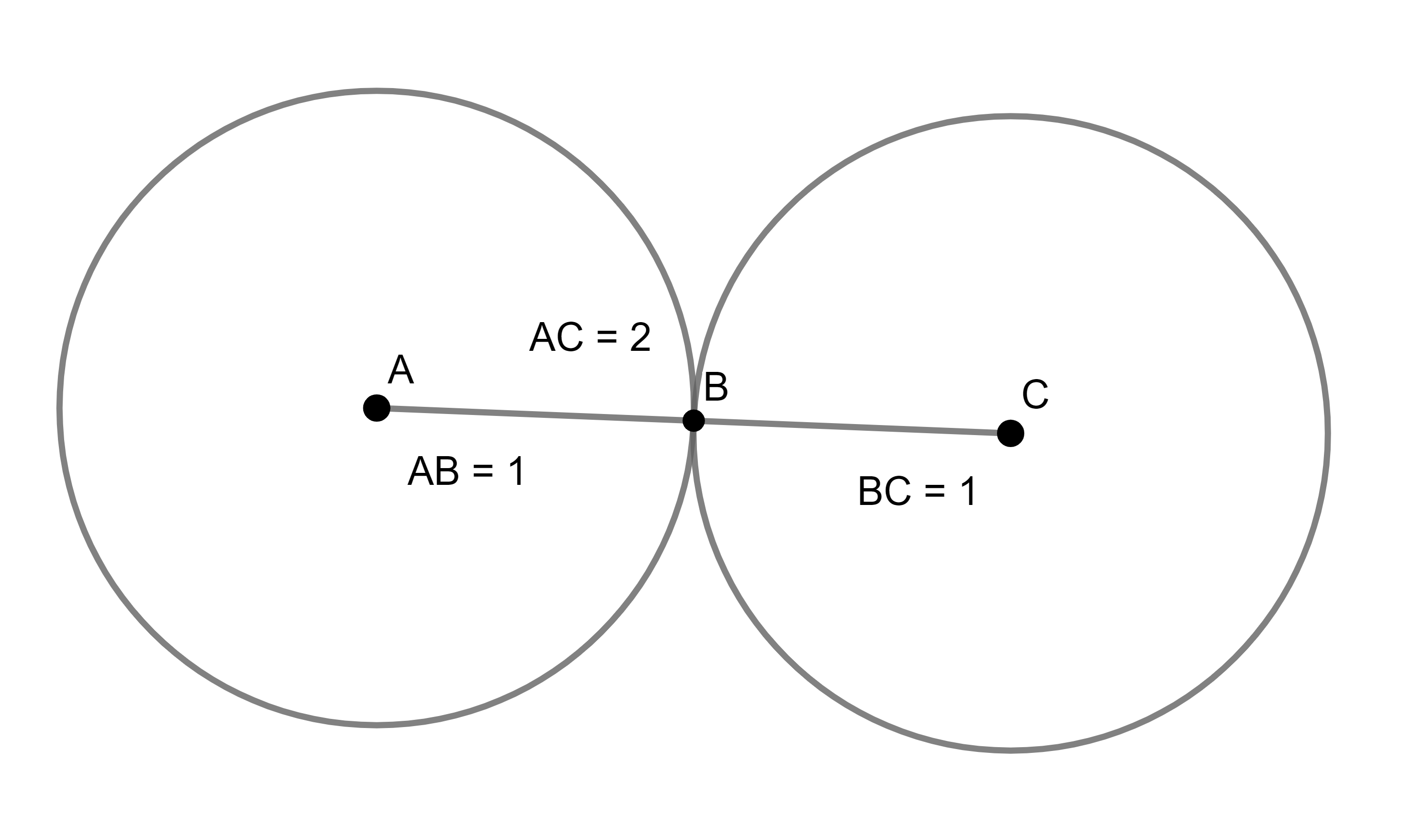
      A teda priama dĺžka AC je naozaj kratšia ako 2\, \text{cm} i keď obvodová dĺžka je 2\, \text{cm}. Ak trojuholníkovú nerovnosť nepoznáte, tak sa neváhajte pohrať s pravítkom a ceruzkou, skúste si nakresliť trojuholník so stranami dlhými 3\, \text{cm},\, 5\, \text{cm},\, 9\, \text{cm} a potom 1\, \text{cm},\, 1\, \text{cm},\, 2\, \text{cm}, či 2\, \text{cm},\, 2\, \text{cm},\, 3\, \text{cm}. Skúste aj iné, uvidíte, ktoré sa vám nakresliť podarí, ktoré nie. No vo všeobecnosti platí, že keď je súčet 2 kratších strán menší ako najdlhšia strana, tak nie sú dosť dlhé na to, aby na seba “dočiahli“. Môžete to vidieť aj na obrázkoch.

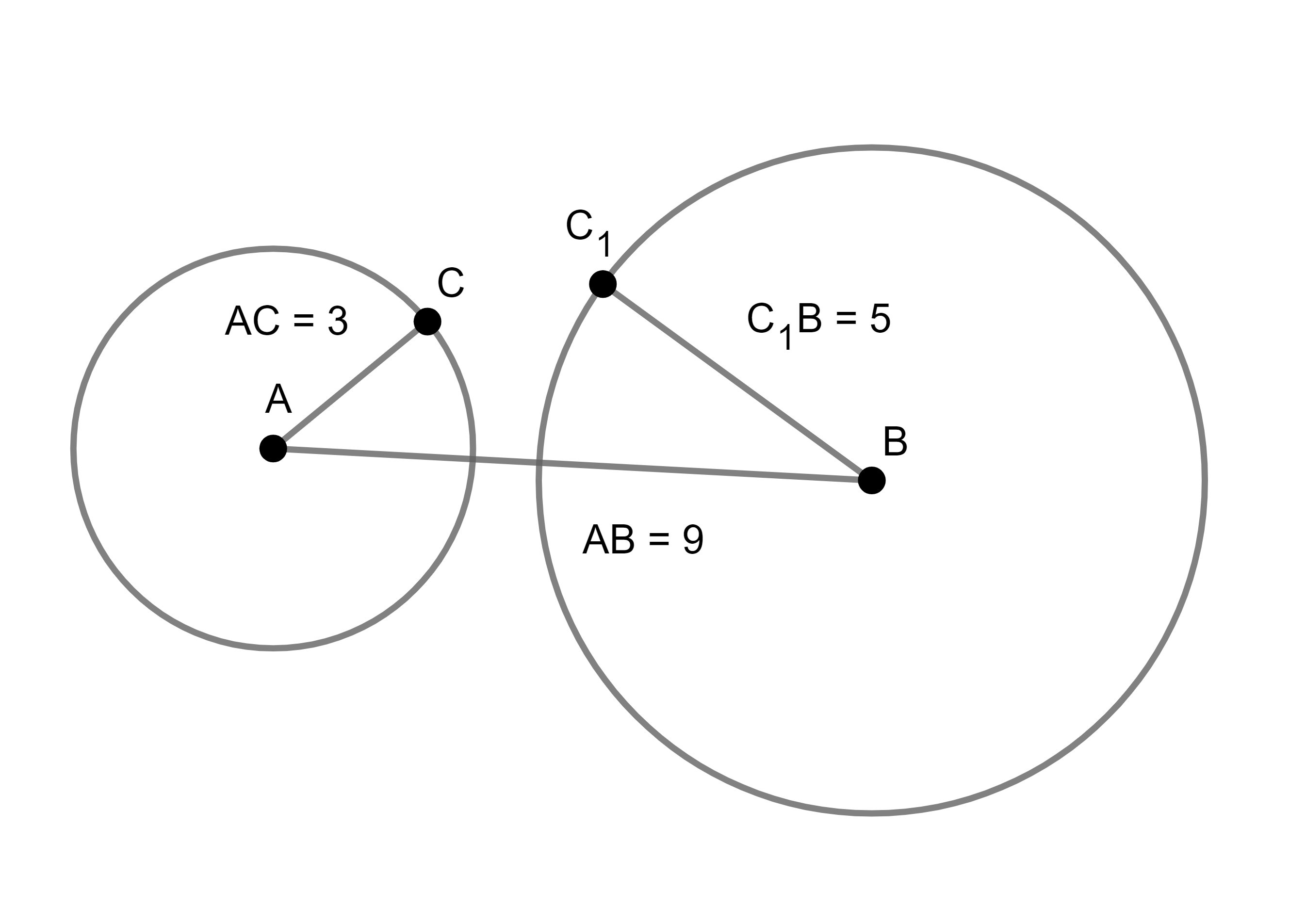
Nech si teda zvolíme rozloženie vrcholov nášho 27–uholníka v 80–uholníku ľubovoľne, tak aspoň 1 strana bude mať dĺžku menšiu ako 2\, \text{cm}.

Komentár

Väčšina z vás príklad zvládla veľmi pekne. Chyby najčastejšie vyplývali z toho, že ste buď vôbec, alebo nedostatočne zdôvodnili, prečo ak je obvodová vzdialenosť dvoch bodov 2\, \text{cm}, tak ich skutočná vzdialenosť musí byť menšia. Poprípade niektorí nezdôvodnili, prečo aspoň 1 zo strán 27–uholníka pri ľubovoľnom výbere vrcholov, musí mať obvodovú vzdialenosť menšiu ako 2\, \text{cm}.