10. príklad - Vzorové riešenie

Kategórie:
5
6
7
8
9

Zadanie

Máme štvorec ABCD. Pre každý jeho vnútorný bod alebo bod na jeho obvode vieme určiť súčet druhých mocnín vzdialeností do všetkých vrcholov tohto štvorca. Chýry hovoria, že v niektorom z bodov, ktoré majú tento súčet najväčší sa nachádza knižnica. Zistite, v ktorých bodoch dostaneme najväčší súčet.

Vzorové riešenie

Opravovali: elusq, erik

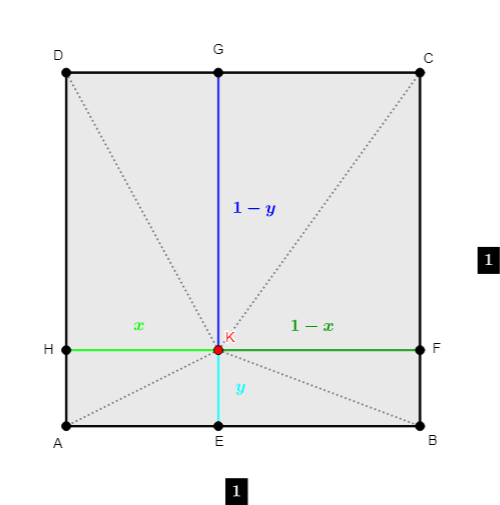
Zo zadania knižnica môže byť v ľubovoľnom bode štvorca alebo na obvode štvorca ABCD, tak nech je v bode K. Veďme rovnobežky so stranami štvorca cez bod K a priesečníky so stranami označíme E,\, F,\, G,\, H v poradí. Vzniknuté štvoruholníky AEKH,\, EBFK,\, KFCG,\, HKGD budú obdĺžnikmi, keďže strany štvorca sú na seba kolmé a rovnako aj na priamky precházdajúce cez bod K.

Môžeme si určiť dĺžku strany štvorca 1. Pre ľubovoľnú inú stranu, by sme všetky dĺžky prenásobili jej dĺžkou a počítali rovnako. Takto si zjednodušíme prácu. Ďalej nech obdĺžnik AEKH má dĺžky strán x a y. Keďže ABCD je štvorec, tak vieme vyjadriť všetky dĺžky strán zvyšných obdĺžnikov s vrcholom K, tak ako vidno na obrázku.

Vzdialenosť bodu K od vrcholov vieme vyrátať vďaka Pytagorovej vete, keďže trojuholníky sú pravouhlé. Napíšme si výraz, ktorý bude súčtom vzdialeností bodu K od vrcholov:

x^2 + y^2 + (1-x)^2 + y^2 + x^2 + (1-y)^2 + (1-x)^2 + (1-y)^2 = \\ = 4 \cdot x^2 + 4 \cdot y^2 - 4 \cdot x - 4 \cdot y + 4 = \\ = 4 \cdot (x^2 + y^2 - x - y + 1) = \\ = 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1)

Na to, aby v tomto bode mohla byť knižnica, musí platiť, že hodnota výrazu 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1) bude najväčšia možná, teda musíme určiť pre aké x a y má výraz najväčšiu možnú hodnotu. Keďže x a y sú od seba nezávislé, môžeme im určiť najväčšiu možnú hodnotu samostatne.

Na začiatku sme si určili stranu štvorca 1 a bod K vnútri alebo na obvode štvorca. Pre dĺžku x bude platiť 0 \leq x \leq 1, teda výraz x-1 je menší alebo rovný 0. Súčin kladného a záporného čísla je záporný. Z toho vyplýva, že hodnota x \cdot (x-1) nemôže byť kladná, lebo platí 0 \leq x \leq 1 a -1 \leq x \leq 0, ale môže byť 0. Preto najväčšia hodnota, ktorú môže nadobúdať výraz x \cdot (x-1) je 0. To nastáva v prípadoch, keď sa buď x = 0 alebo x-1 = 0. Konečne dostávame, že x \in \lbrace 0,1 \rbrace, čo je práve vtedy, keď bod K leží na priamke AD alebo BC.

Podobným spôsobom sa vieme dopracovať k y \in \lbrace 0, 1 \rbrace, teda že bod K leží na primake AB alebo CD.

Ako sme spomínali, aby hodnota 4 \cdot (x \cdot (x-1) + y \cdot (y-1) + 1) bola čo najväčšia, tak musí byť každá časť výrazu, čo najväčšia, teda x a y musia byť rovné 0 alebo 1.
To nám dáva štyri možnosti kde môže byť knižnica:

  • x=0 a y=0, čo je prienik AB a AD \to v bode A
  • x=0 a y=1, čo je prienik AB a BC \to v bode B
  • x=1 a y=0, čo je prienik CD a AD \to v bode D
  • x=1 a y=1, čo je prienik CD a BC \to v bode C

Odpoveď: Najväčšia hodnota bude vo vrcholoch štvorca, teda knižnica sa nachádza v niektorom z nich.