6. príklad - Vzorové riešenie

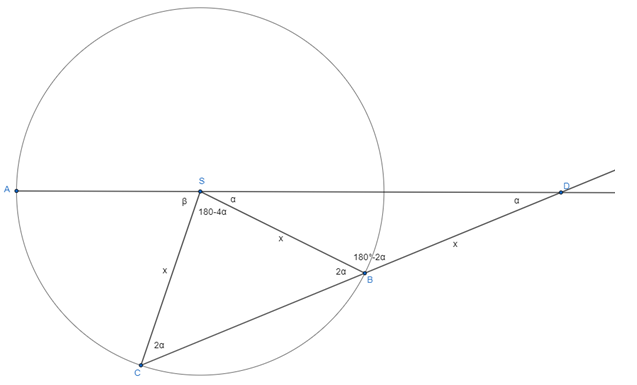
Označíme si \measuredangle SDB ako \alpha a \measuredangle ASC ako \beta. Vieme, že úsečky SC a SB sú obe polomerom kružnice a taktiež zo zadania vieme, že úsečka SC je rovnako dlhá ako úsečka BD. To znamená, že |SC|=|SB|=|BD|=x.

Keďže je \triangle SDB rovnoramenný, tak \measuredangle SDB a \measuredangle BSD sú zhodné. Súčet vnútorných uhlov v trojuholníku je 180°, v \triangle SDB bude teda \measuredangle DBS=180°- \measuredangle SDB- \measuredangle BSD a keď namiesto zhodných uhlov \measuredangle SDB a \measuredangle BSD dosadíme \alpha, tak dostaneme \measuredangle DBS=180°-2\alpha.

Vieme, že \measuredangle SBC a \measuredangle DBS sú susedné uhly a teda platí:

\measuredangle SBC+\measuredangle DBS=180°

\measuredangle SBC+180°-2\alpha=180°

\measuredangle SBC=2\alpha

Keďže je \triangle SBC rovnoramenný, tak \measuredangle SBC a \measuredangle BCS sú zhodné, čiže \measuredangle BCS=2\alpha. Súčet vnútorných uhlov v trojuholníku je 180°, teda \measuredangle CSB=180°-4\alpha

Vieme, že \measuredangle ASD=180°, potom tiež platí:

\alpha+\beta+\measuredangle CSB=180°

\measuredangle CSB=180°-\alpha-\beta

Našli sme dve možnosti na vyjadrenie \measuredangle CSB, dáme si ich teda do rovnosti.

180°-\alpha-\beta=180°-4\alpha

-\alpha-\beta=-4\alpha

\beta=3\alpha

Odpoveď: Pomer veľkosti \measuredangle ASC a \measuredangle SDB je 3:1.

Komentár

V tomto príklade existovali dve možné polohy bodu A. Jedna ako v našom riešení, kde bod S leží medzi A a D, druhá ako na obrázku nižšie, kde A leží medzi S a D.

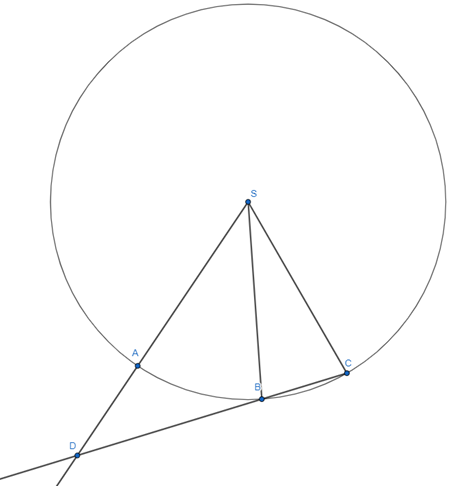
Príklad sa aj v takomto prípade riešil rovnako, líšilo by sa len jedno vyjadrenie \measuredangle CSB, ktoré by vyšlo \beta - \alpha namiesto 180° - \alpha - \beta a samozrejme výsledok (\beta = 180° - 3\alpha), ktorý by sa nedal vyjadriť ako pomer.

Úplne správne riešenie by malo obsahovať obe možnosti, keďže sa však postup nelíšil, body sme nestrhávali, ak ste poslali len jednu z nich. Najmä vo vyšších kategóriách matematickej olympiády si na to však treba dávať pozor.