Odporúčaný článok

Riešky výlet - Ahojte Rieškari, zoberte batohy, úsmevy, dobré nálady, lopty, hry, frisbee, kamarátov… a poďte s nami na výlet! Poprechádzame sa po Malých Karpatoch, kde pre vás máme pripravený skvelý program a … Prejsť na článok

×

Prémia 1

Koniec: 04. november 2019 22:00
Do konca: kolo skončilo
Kategórie:
5
6
7
8
9
Tento príklad je iný ako ostatné. Nemusíš spisovať svoj postup, stačí nám poslať riešenie. Viac informácií nájdeš v pravidlách.

Zadanie

Tento príklad je iný ako ostatné. Nemusíš spisovať svoj postup, stačí nám poslať riešenie. Viac informácií nájdeš v pravidlách.
Havoš má veľmi rád čokoládu. Doktor mu ale povedal, že má alergiu na mlieko, či čo to, a že by mal prestať jesť toľko čokolády. Havoš odvtedy nikdy nezjedol celú čokoládu, ale vždy si nechal kúsok tvorený práve piatimi dielikmi. Teraz ich už má všetkých dvanásť rôznych, tak sa s nimi začal hrať. Má štvorčekovú mriežku 42\times42 štvorčekov a 12 dielikov pentomín (viď obrázok). Pentominá chce vložiť do mriežky tak, aby ohraničili, čo najviac políčok. Ohraničené políčka môžu susediť stranou alebo rohom jedine s iným ohraničeným políčkom, alebo políčkom prekrytým niektorým pentominom. Dieliky môže ľubovoľne otáčať alebo preklopiť, nemôže však použiť ten istý viackrát. Pomôžte Havošovi nájsť také rozloženie pentomín, ktoré ohraničí čo najväčší počet políčok.
Vzorové riešenie Odovzdať

Komentáre (4)

  • Majko
    26. október 2019 16:50

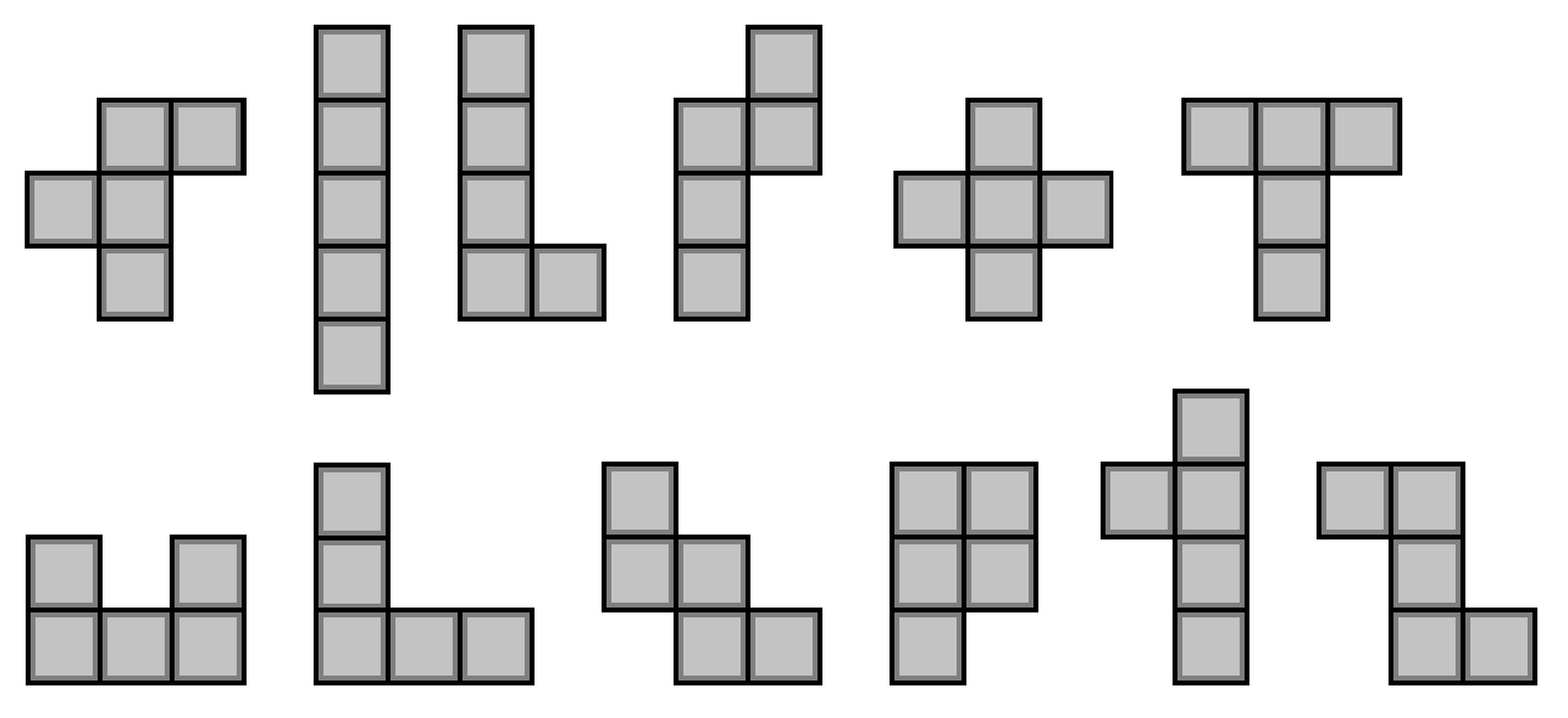
    Ak políčko susedí s pentonimami, inými políčkami a krajom, je ohraničené?

  • mišo Vedúci
    26. október 2019 17:28

    Ahoj,
    políčka susediace s okrajom mriežky nie sú ohraničené.
    Mišo

  • MatejBachnicek
    02. november 2019 12:08

    Dobrý deň,
    sú políčka pentomina ohraničené políčka, ak dodržiavajú to, že susedia len s iným ohraničeným políčkom alebo políčkom pentomina?

  • mišo Vedúci
    02. november 2019 12:42

    Ahoj,
    políčka prekryté pentominami nie sú ohraničené.

    Mišo

Pridaj komentár

Pridať komentár môžeš iba keď si prihlásený!

Prihlásiť sa