Odporúčaný článok
Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok
×7. príklad - Vzorové riešenie
Kategórie:
5
6
7
8
9
Zadanie
Majme rovnobežník ABCD a stredy jeho strán M_{AB}, M_{BC}, M_{CD}, M_{DA}. Ďalej spravíme kružnice k_1, k_2 tak že majú stredy postupne v M_{AB}, M_{CD} a polomery |M_{CD} M_{BC}|, |M_{AB} M_{BC}|. Ukážte, že tieto dve kružnice sa pretínajú v bode M_{DA} a na priamke BC.
Vzorové riešenie
Opravovali: JozefMican, ula, šálka
Čo už poznáme:
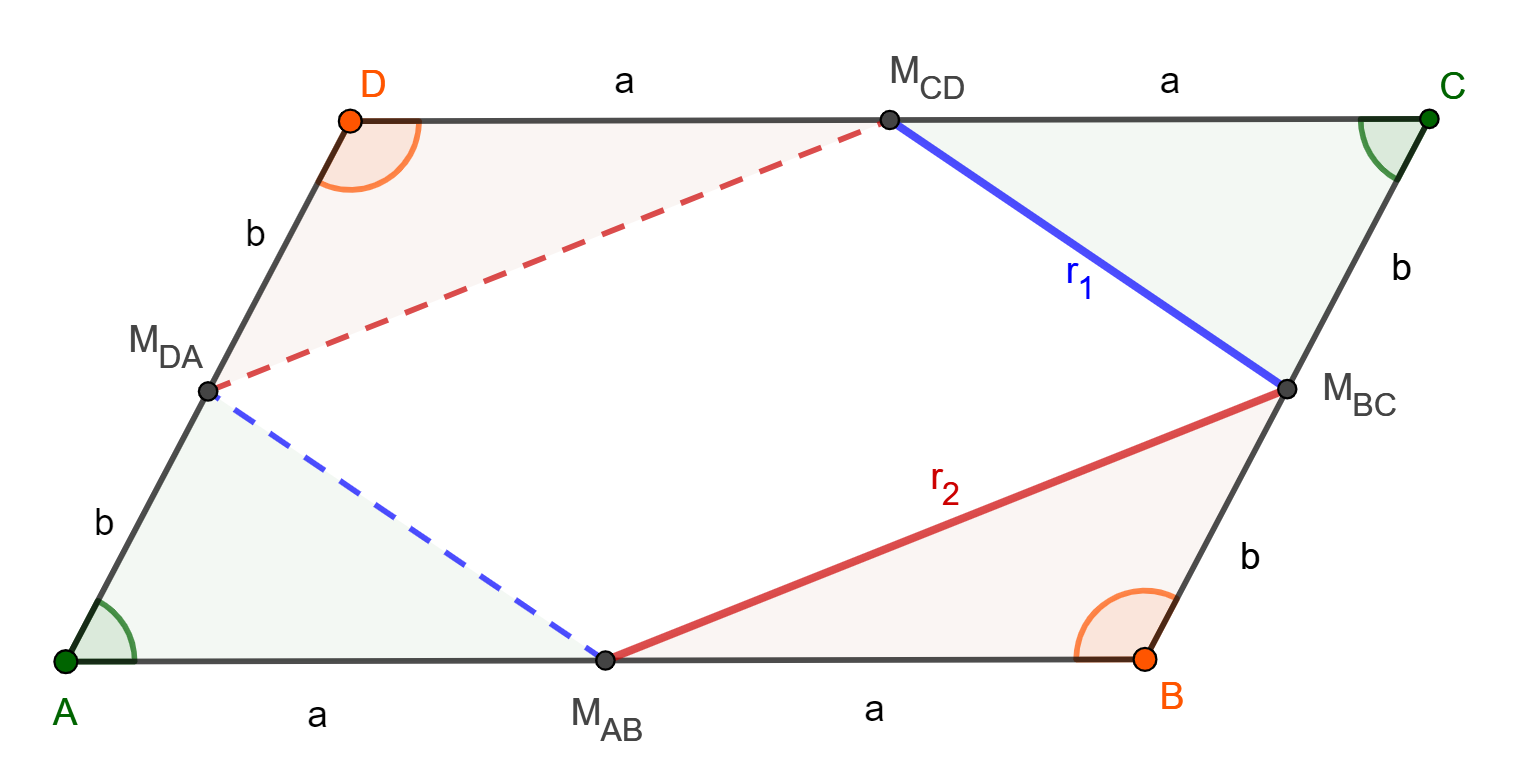
Ako prvé si zopakujeme čo vieme o rovnobežníkoch. Vo všeobecnom rovnobežníku sú protiľahlé strany rovnobežné a rovnako dlhé. Zároveň vieme, že protiľahlé vnútorné uhly sú rovnako veľké a najznámejšie rovnobežníky sú štvorec, obdĺžnik a kosoštvorec, avšak aby sme sa vyhli špeciálnym prípadom, naďalej budeme brať v úvahu iba kosodĺžnik, respektíve všeobecný rovnobežník, tak ako ho máme zadaný v zadaní:
Riešenie:
M_{AB}, M_{BC}, M_{CD} a M_{DA} sú stredy strán rovnobežníka ABCD, takže rozdelujú každú stranu na dve polovice, pričom vďaka rovnosti protiľahlých strán, možeme tvrdiť, že:
a = \left|AM_{AB}\right| = \left|M_{AB}B\right| = \left|DM_{CD}\right| = \left|M_{CD}C\right|
b = \left|BM_{BC}\right| = \left|M_{BC}C\right| = \left|DM_{DA}\right| = \left|M_{DA}A\right|
Z vety o zhodnosti dvoch trojuholníkov podľa SUS (strana, uhol, strana) vieme vyhlásiť trojuholníky △M_{DA}AM_{AB} a △M_{BC}CM_{CD} za zhodné a to isté o dvojici trojuholníkov △M_{AB}BM_{BC} a △M_{CD}DM_{DA}. V takom prípade ich tretie strany majú rovnakú dĺžku a r_1 = \left|M_{CD}M_{BC}\right| = \left|M_{DA}M_{AB}\right| zatiaľčo r_2 = \left|M_{AB}M_{BC}\right| = \left|M_{DA}M_{CD}\right|. Nezabúdajme, že stred kružnice k_1 je v M_{AB} a stred kružnice k_2 je v M_{CD}. Obe kružnice so svojím príslušným polomerom budú teda zákonite prechádzať bodom M_{DA}, čím sme dokázali prvú časť úlohy.
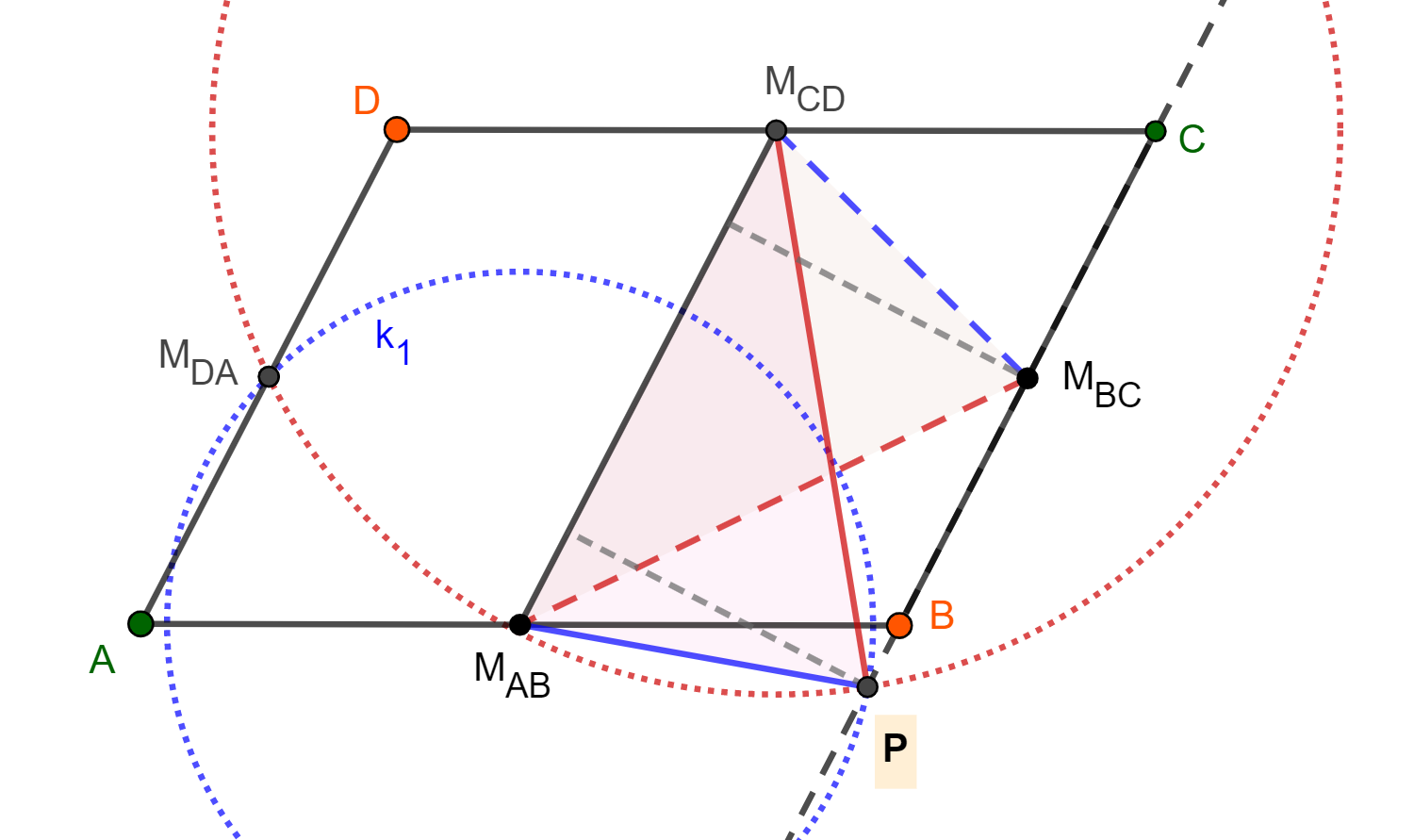
Pozrime sa teraz na druhý priesečník kružníc k_1 a k_2 (pre jednoduchosť si ho označme P). Pri porovnávaní trojuholníkov △M_{AB}M_{CD}P a △M_{AB}M_{CD}M_{BC} si môžeme povšimnúť, že podľa vety o zhodnosti dvoch trojuholníkov podľa SSS (strana, strana, strana), tieto dva trojuholníky sú zhodné, akurát sú zrkadlovo otočené. Ak sa jedna z ich strán zhoduje, tak aj výška na túto stranu bude u oboch trojuholníkov totožná, preto vieme, že výška na stranu M_{AB}M_{CD} u jedného trojuholníku prechádzajúca cez vrchol M_{BC} a u druhého cez vrchol P je rovnaká. Predĺžená priamka M_{AB}M_{CD} sa nachádza rovnobežne ležiaca uprostred priamky AD a priamky BC, kedže M_{AB} aj M_{CD} sa nachádzajú uprostred strán pôvodného rovnobežníka. Ak je teda M_{BC} vzdialený od M_{AB}M_{CD} toľko čo je vzdialená rovnobežka BC ku priamke M_{AB}M_{CD}, tak aj bod P aby bol rovnako vzdialený od M_{AB}M_{CD} musí ležať na priamke BC.
Komentár: Veľa z vás zabudlo na začiatku aspoň zmieniť na základe čoho považujete niečo za zhodné/podobné/rovnobežné/rovnako dlhé/... Spôsobov ako riešiť túto úlohu bolo hneď niekoľko, riešenie ktoré sme tu uviedli bolo jedno z tých častejších. Pre tých, ktorí sa pokúšali využiť pravidlá súmernosti, skúste si oprášiť vedomosti a zopakovať si rozdiel medzi osovou a stredovou súmernosťou.
Určite chceme pochváliť všetkých ktorý si dali záležať na správnom zápise geometrických vzťahov pomocou rovníc alebo na to určených špeciálnych znakov, aspoň tak ako to máme my tu pri rozmeroch a vzdialenostiach úsečiek a strán. Ak si neviete rady s digitálnym kreslením geometrie alebo jednoducho neviete tak presne kresliť, tak odporúčame využiť GeoGebru, ktorá má aj online verziu použiteľnú z webového prehliadača a tak nemusíte nič inštalovať.
Bodovanie: Riešenie úlohy sme rozdelili na dve časti za rovnaký počet bodov, prvá bola dokázať že sa kružnice k_1 a k_2 pretínajú v M_{DA} a druhá časť bola o polohe druhého priesečníku týchto kružníc (dokázať že leží na priamke BC).

Riešenie:
M_{AB}, M_{BC}, M_{CD} a M_{DA} sú stredy strán rovnobežníka ABCD, takže rozdelujú každú stranu na dve polovice, pričom vďaka rovnosti protiľahlých strán, možeme tvrdiť, že:
a = \left|AM_{AB}\right| = \left|M_{AB}B\right| = \left|DM_{CD}\right| = \left|M_{CD}C\right|
b = \left|BM_{BC}\right| = \left|M_{BC}C\right| = \left|DM_{DA}\right| = \left|M_{DA}A\right|
Z vety o zhodnosti dvoch trojuholníkov podľa SUS (strana, uhol, strana) vieme vyhlásiť trojuholníky △M_{DA}AM_{AB} a △M_{BC}CM_{CD} za zhodné a to isté o dvojici trojuholníkov △M_{AB}BM_{BC} a △M_{CD}DM_{DA}. V takom prípade ich tretie strany majú rovnakú dĺžku a r_1 = \left|M_{CD}M_{BC}\right| = \left|M_{DA}M_{AB}\right| zatiaľčo r_2 = \left|M_{AB}M_{BC}\right| = \left|M_{DA}M_{CD}\right|. Nezabúdajme, že stred kružnice k_1 je v M_{AB} a stred kružnice k_2 je v M_{CD}. Obe kružnice so svojím príslušným polomerom budú teda zákonite prechádzať bodom M_{DA}, čím sme dokázali prvú časť úlohy.

Pozrime sa teraz na druhý priesečník kružníc k_1 a k_2 (pre jednoduchosť si ho označme P). Pri porovnávaní trojuholníkov △M_{AB}M_{CD}P a △M_{AB}M_{CD}M_{BC} si môžeme povšimnúť, že podľa vety o zhodnosti dvoch trojuholníkov podľa SSS (strana, strana, strana), tieto dva trojuholníky sú zhodné, akurát sú zrkadlovo otočené. Ak sa jedna z ich strán zhoduje, tak aj výška na túto stranu bude u oboch trojuholníkov totožná, preto vieme, že výška na stranu M_{AB}M_{CD} u jedného trojuholníku prechádzajúca cez vrchol M_{BC} a u druhého cez vrchol P je rovnaká. Predĺžená priamka M_{AB}M_{CD} sa nachádza rovnobežne ležiaca uprostred priamky AD a priamky BC, kedže M_{AB} aj M_{CD} sa nachádzajú uprostred strán pôvodného rovnobežníka. Ak je teda M_{BC} vzdialený od M_{AB}M_{CD} toľko čo je vzdialená rovnobežka BC ku priamke M_{AB}M_{CD}, tak aj bod P aby bol rovnako vzdialený od M_{AB}M_{CD} musí ležať na priamke BC.
Komentár: Veľa z vás zabudlo na začiatku aspoň zmieniť na základe čoho považujete niečo za zhodné/podobné/rovnobežné/rovnako dlhé/... Spôsobov ako riešiť túto úlohu bolo hneď niekoľko, riešenie ktoré sme tu uviedli bolo jedno z tých častejších. Pre tých, ktorí sa pokúšali využiť pravidlá súmernosti, skúste si oprášiť vedomosti a zopakovať si rozdiel medzi osovou a stredovou súmernosťou.
Určite chceme pochváliť všetkých ktorý si dali záležať na správnom zápise geometrických vzťahov pomocou rovníc alebo na to určených špeciálnych znakov, aspoň tak ako to máme my tu pri rozmeroch a vzdialenostiach úsečiek a strán. Ak si neviete rady s digitálnym kreslením geometrie alebo jednoducho neviete tak presne kresliť, tak odporúčame využiť GeoGebru, ktorá má aj online verziu použiteľnú z webového prehliadača a tak nemusíte nič inštalovať.
Bodovanie: Riešenie úlohy sme rozdelili na dve časti za rovnaký počet bodov, prvá bola dokázať že sa kružnice k_1 a k_2 pretínajú v M_{DA} a druhá časť bola o polohe druhého priesečníku týchto kružníc (dokázať že leží na priamke BC).