Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×7. príklad - Vzorové riešenie
Zadanie
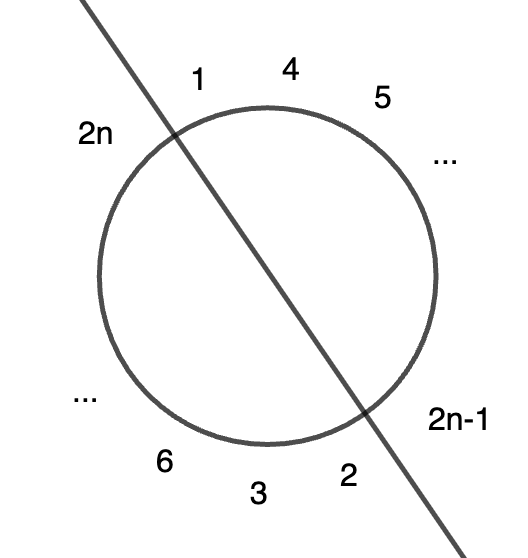
Starček má 2n kronov s číslami od 1 až po 2n. Usporiadal ich do kruhu v nejakom poradí. Z nich potom povytváral všetky možné súčty tak, že vždy sčítal dohromady nejakých n susedných čísel (dohromady teda vytvoril 2n súčtov).
Pre každé n určte, koľko najmenej rôznych súčtov mohol takto dostať, ak usporiadal čísla do kruhu optimálne.
Príklad: ak by sa n rovnalo 3, starček by mohol vytvoriť kruh 5, 3, 4, 6, 1, 2, (znova 5)... a súčty by boli:
- 5+3+4=12
- 3+4+6=13
- 4+6+1=11
- 6+1+2=9
- 1+2+5=8
- 2+5+3=10
Vzorové riešenie
Pri takýchto úlohách býva často najťažšie nájsť koľko vôbec má byť odpoveď. Potom dôkaz, že menej to byť nemôže už väčšinou nie je až taký hrozný ale aj tak je nutný a popri tom si naozaj viete overiť, že máte správnu odpoveď. A potom ešte môže byť ťažké nájsť nejakú konštrukciu na to aby sme dokázali, že naozaj vieme dosiahnuť takú hodnotu. Táto posledná časť ale môže často plynúť z nášho postupu.
Za prvé skúsme odhadnúť koľko rôznych súčtov musíme najmenej mať. Najjednoduchšie je keby bol len jeden. Je ale možné aby sme mali len jeden?
Ako sa ukáže, nie je. Dôkaz je celkom jednoduchý.
Pozrime sa na nejakých
n po sebe idúcich čísiel a_1,a_2,\dots,a_n. Označme si ich súčet S
Potom sa pozrime na vedľajšiu n-ticu čísiel a_2,a_3,\dots,a_{n+1}. Všimnime si že súčet týchto čísiel je len S-a_1+a_{n+1}. Toto sa ale nemôže rovnať S, lebo zo zadania a_1,a_{n+1} sú nutne rôzne čísla.
No dobre, tak jedna nie je odpoveďou, ale dva rôzne súčty by niekedy mohli fungovať. Čo ak by
n bolo nepárne?
No ak by n bolo nepárne, tak súčet všetkých čísiel by bol 1+2+ \dots + 2n=\frac{2n(2n+1)}{2}=n(2n+1) čo je zjavne nepárne. Teda kebyže sa pozrieme na nejaké 2 polovice, ktoré nezdieľajú čísla, teda rozdelíme kruh na pol. Tieto opačné polovice dávajú dohromady všetky čísla, ktorých súčet je nepárny, teda jedna polka je párna a druhá nepárna. Napríklad rozdelme čísla postupne do dvojíc, ktorých rozdiel je 1, teda myslíme tým:
(1,2),(3,4), \dots , (2n-1, 2n)
Následne rozdelme ich tak, že čísla z dvojice dáme oproti sebe, a následne striedame, či dáme menší prvok z dvojice alebo väčší. Myslíme tým nasledovné:
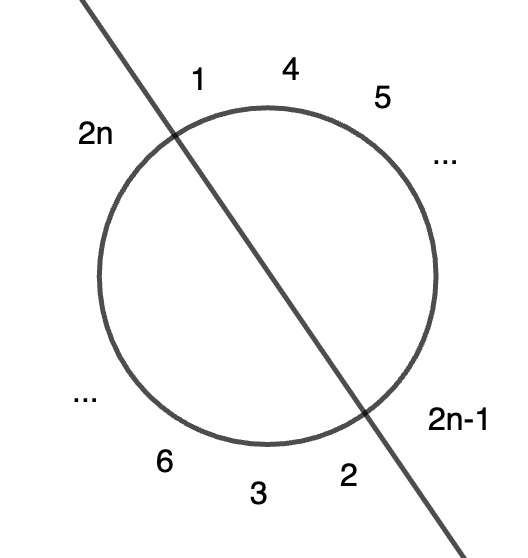
Nie je tažké overiť, že tieto dve polky majú súčty ktoré sa líšia o 1
Teraz si uvedomme, že kebyže posunieme rozdeľ o jedno miesto, tak vždy k jednej pólke prirátame 1 a od druhej odrátame. Zároveň to, že kedy sa pridáva a kedy odrátava sa naozaj strieda.
Teda konkrétne nejaké čísla a_k,a_{k+1},\dots ,a_{k+n-1} dávajú dokopy nejaký súčet S.
Pozrime sa na čísla o miesto vedľa, teda
a_{k+1},a_{k+2},\dots ,a_{k+n}. Ich súčet je:
a_{k+1}+a_{k+2}+\dots +a_{k+n} = S-a_k+a_{k+n}
Všimnime si, že keďže sme dali naproti sebe čísla, ktoré majú rozdiel 1, tak aj výsledok sa zmení o \pm 1
Všimnime si ale, že niečo podobné nebude fungovať pre párne n. Označme si znovu súčet všetkých čísiel M. Potom kebyže si rozdelíme znova kruh na dve rôzne pólky, ich súčet je dokopy M, a teda ich samostatné súčty sú nejaké k a M-k.
Za prvé, čo by sa stalo kebyže sú to rovnaké čísla? Povedzme že
a_1+ a_2+ \dots + a_n = a_{n+1}+a_{n+2}+ \dots + a_{2n}=\frac{M}{2}
Potom vieme, že a_2+a_3+ \dots + a_{n+1} = \frac{M}{2} -(a_1-a_{n+1}) \\ a_{n+2}+a_{n+3}+ \dots + a_{1} = \frac{M}{2} +(a_1-a_{n+1})
Toto sú zjavne dva rôzne súčty, ktoré sa ani nerovnajú pôvodnému a teda by sme mali až tri súčty.
No dobre ale čo keby sme rozdelili tie strany na 2 rôzne súčty a jednoducho by sa striedali? Povedzme bez ujmy na všeobecnosti, že a_1+a_2+ \dots + a_n=k.
Potom a_{n+1}+a_{n+2}+ \dots + a_{2n}=M-k čo sú dva rôzne súčty.
Kedže chceme aby sme mali len 2 a susedné súčty vieme, že sa nerovnajú, tak zjavne musí platiť, že:
a_2+a_2+ \dots + a_{n+1}=M-k \\ a_{n+2}+a_{n+3}+ \dots + a_1=k
A potom zase
a_3+a_4+ \dots + a_{n+2}=k \\ a_4+a_5+ \dots + a_{n+3}=M-k
A tak ďalej. Problém nastáva v tom, že každé dva "kroky" máme rovnaký súčet. A s tým je zle to, že po n krokoch (n je teraz párne a teda sa tam dostaneme po párnom počte krokov!) máme dostať súčet a_{n+1}+a_{n+2}+\dots +a_{2n}=M-k \neq k. No a to je spor.
Teda pri párnych n nemôžeme mať len dva súčty, ale môžeme skúsiť, či nevieme spraviť tri.
A naozaj ide to, môžeme spraviť veľmi podobnú konštrukciu ako pre nepárne n a vzniknú tri rôzne súčty - \frac{M}{2}-1, \frac{M}{2} a \frac{M}{2}+1 .