Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×1. príklad
Zadanie
Lukáš a Alex na lodi skladujú buď chleby, alebo ovocie. Toto jedlo sa nachádza buď v kuchynke, alebo v sklade. Lukáš si pamätá, že najprv videl v kuchynke iba 1 chlieb. Potom však v meste vymenili všetky chleby z kuchyne za toľko isto kúskov ovocia. Následne chlapci odniesli polovicu ovocia z kuchynky do skladu. Vtedy boli v kuchynke 2 kúsky jedla a v sklade 8. Chlapci však potom vyniesli do kuchyky všetky chleby zo skladu, a vtedy narátali v kuchynke až 6 kúskov jedla. Koľko bolo čoho kde na začiatku?
Vzorové riešenie
Na začiatok sa pozrime na jednotlivé udalosti a pozrime sa ako sa nám zmení celkový počet kusov jedla:
- Videl v kuchynke iba 1 chlieb - Celkový počet jedla sa nezmenil
- Vymenili všetky chleby z kuchyne za toľko isto kúskov ovocia - vymenili za rovnaký počet takže celkovo sa počet jedla nezmenil
- Chlapci odniesli polovicu ovocia z kuchynky do skladu - Jedlo sa len presunulo ale celkovo sa počet nezmenil
- V kuchynke boli 2 kúsky jedla a v sklade 8 - Nemenili sme počet, len sme zrátali, že dokopy je 10 kúskov jedla.
- Vyniesli do kuchyky všetky chleby zo skladu - Jedlo sa znovu len presunulo
- Narátali v kuchynke až 6 kúskov jedla - Zas sme nemenili počet.
Môžeme si všimnúť, že počet kusov jedla sa nikdy nezmenil a teda dokopy budeme mať vždy 10 kusov.
Ako prvé sa pozrime na udalosti 4, 5 , 6
Najprv vieme, že pred presunom chlebov boli v kuchynke 2 kusy jedla. Potom tam pribudli všetky chleby zo skladu a bolo ich spolu 6. To znamená, že v sklade museli byť 4 chleby. A keďže v sklade bolo dokopy 8 kusov, zvyšné museli byť 4 ovocia.
Takže pred presunom chlebov boli v sklade 4 chleby a 4 ovocia. Zároveň vieme aj, že počet ovocia v sklade sa až do konca už nezmenil.
Aby sme sa lepšie vyznali v tom koľko máme čoho tak si spravíme tabuľku počtov jedál:
| Chleby kuch. | Ovocie kuch. | Chleby sklad | Ovocie sklad | |
|---|---|---|---|---|
| Začiatok | ||||
| po 2. udalosti | ||||
| po 3. udalosti | 4 | 4 | ||
| Na konci | 0 | 4 |
Teraz sa pozrime na udalosti 2 a 3.
Po druhej udalosti sme mali v kuchynke 0 chlebov, pretože všetky chleby sa vymenili za ovocie. Všimnime si, že počet chlebov v kuchyni zostal až do konca stále nulový, až kým sme na samom konci nepriniesli 4 chleby zo skladu.
Keďže bolo stále dokopy 10 kusov jedla, každý riadok tabuľky musí mať súčet 10. Po doplnení toho, čo už vieme ostáva v posledných dvoch riadkoch vždy už len jedno neznáme číslo a to číslo doplníme teda tak aby súčet v riadku bol 10.
| Chleby kuch. | Ovocie kuch. | Chleby sklad | Ovocie sklad | |
|---|---|---|---|---|
| Začiatok | ||||
| po 2. udalosti | 0 | |||
| po 3. udalosti | 0 | 2 | 4 | 4 |
| Na konci | 4 | 2 | 0 | 4 |
Teraz sa pozrime na to, že 3. udalosť bola presunutie polovice ovocia z kuchyne do skladu.
To znamená, že v kuchyni zostala druhá polovica. Túto polovicu už poznáme, sú to 2 kusy ovocia. A keďže 2 kusy sú polovica, pred presunom museli byť v kuchynke 4 kusy ovocia.
A ak sme do skladu presunuli polovicu, teda 2 kusy, v sklade muselo byť predtým o 2 ovocia menej. Takto už vieme doplniť aj druhý riadok v tabuľke.
| Chleby kuch. | Ovocie kuch. | Chleby sklad | Ovocie sklad | |
|---|---|---|---|---|
| Začiatok | ||||
| po 2. udalosti | 0 | 4 | 4 | 2 |
| po 3. udalosti | 0 | 2 | 4 | 4 |
| Na konci | 4 | 2 | 0 | 4 |
Jediné, čo nám ešte zostáva, je pozrieť sa na 2. a 1. udalosť.
Počas 2. udalosti sa všetky chleby v kuchynke vymenili za ovocie. A v 1. udalosti vieme, že Lukáš v kuchynke videl 1 chlieb.
To znamená, že na úplnom začiatku bol v kuchynke 1 chlieb a počet ovocia tam musel byť o 1 kus menší než po 2. udalosti. V tabuľke už vieme, že po 2. udalosti boli v kuchynke 4 kusy ovocia, takže na začiatku tam museli byť 3 kusy ovocia.
Počet vecí v sklade sa medzi udalosťami 1 a 2 nezmenil, takže teraz už vieme doplniť aj 1. riadok tabuľky a tým získame konečnú odpoveď.
| Chleby kuch. | Ovocie kuch. | Chleby sklad | Ovocie sklad | |
|---|---|---|---|---|
| Začiatok | 1 | 3 | 4 | 2 |
| po 2. udalosti | 0 | 4 | 4 | 2 |
| po 3. udalosti | 0 | 2 | 4 | 4 |
| Na konci | 4 | 2 | 0 | 4 |
Odpoveď: Na začiatku bol v kuchynke 1 chleba a 3 ovocia a v sklade 4 chleby a 2 ovocia.
2. príklad
Zadanie
Na vzducholodi sa rýchlosť nastavuje nasledovne: chlapci majú niekoľko vrtúľ, pričom zapojených je vždy niekoľko z nich (môžu byť aj všetky). Každá zapojená vrtuľa poháňa loď kladnou celočíselnou rýchlosťou dopredu alebo dozadu. Ak sú dve vrtule zapojené do rovnakého smeru, ich pohon sa sčíta, a ak do opačného, ich pohon sa odčíta. Chlapci vedia so svojimi vrtuľami dosiahnuť ľubovoľnú celočíselnú rýchlosť od 1 do 13 (vrátane). Koľko najmenej môžu mať vrtúľ? Aký môžu mať tieto vrtule pohon? Ukážte, že menej vrtúľ naozaj nemôžu mať.
Vzorové riešenie
Máme zistiť koľko najmenej môže byť vrtúľ. Oplatí sa teda skúšať od najmenších čísel.
- rýchlosťou 1 dopredu
- stáť
- rýchlosťou 1 dozadu
- rýchlosťou A dopredu
- stáť
- rýchlosťou A dozadu
| Dopredu | Dozadu |
|---|---|
| A+B ak idú obe vrtule dopredu | A+B ak idú obe vrtule dozadu |
| A ak ide väčšia vrtuľa dopredu a menšia sa nehýbe | A ak ide väčšia vrtuľa dozadu a menšia sa nehýbe |
| A-B ak ide väčšia vrtuľa dopredu a menšia dozadu | A-B ak ide väčšia vrtuľa dozadu a menšia dopredu |
| B ak ide menšia vrtuľa dopredu a väčšia nehýbe | B ak ide menšia vrtuľa dozadu a väčšia sa nehýbe |
No a okrem toho vie vzducholoď aj stáť.
To znamená, že pre 2 vrtule existuje presne 9 pohybov, akými vie vzducholoď ísť. Takže rýchlosti od 1 do 13 to nepokryje.
Poďme teda na 3 vrtule.
Koľko rôznych pohybov vie byť v tomto prípade?
(Vrelo odporúčam čitateľovi si pár takýchto možností vypísať. Pokojne aj všetky. Je ich dosť, no nie až tak strašne veľa.)
Predstavme si, že vrtule s pohonmi A, B, C. Každá z vrtúľ má tri spôsoby ako vie byť zapojená:
- vie ísť dopredu
- vie byť vypnutá
- vie ísť dozadu
Takže pre vrtuľu s pohonom A sú tri možnosti ako vie ísť. Pre každú z týchto možností existujú tri možnosti ako vieme zapojiť vrtuľu B. Toto si vieme pekne ilustrovať na tomto obrázku:
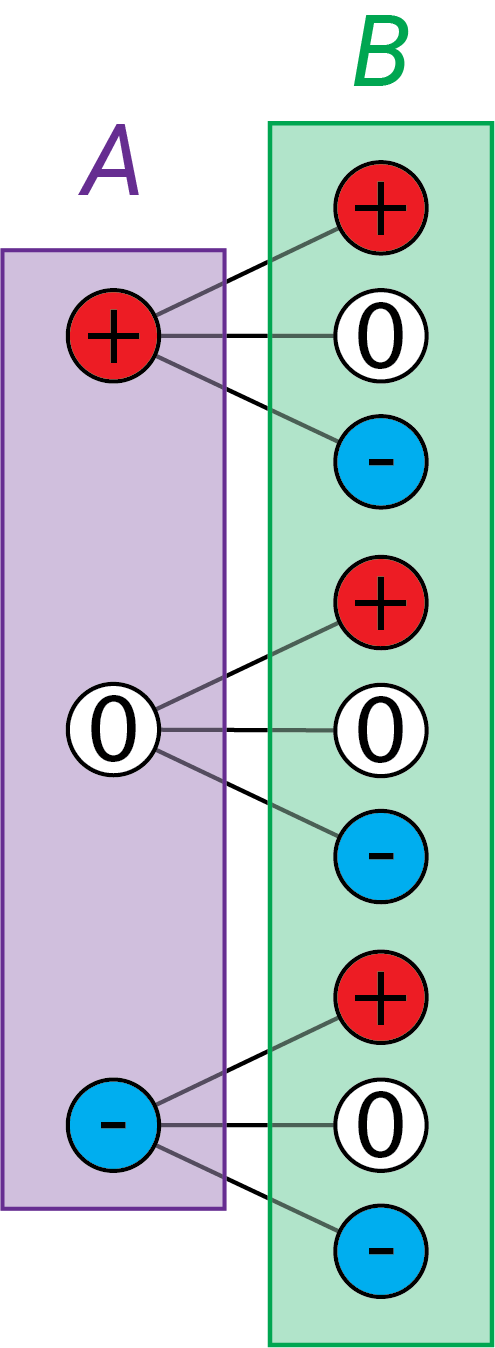
Možnosti zapojenia vrtule A sú vo fialovom rámčeku a každému z nich prislúchajú 3 možnosti zapojenia vrtule B, ktoré sú v zelenom rámčeku. Plus v červenom znamená dopredu, Mínus v modrom znamená dozadu a Nula v bielom znamená, že je vrtuľa vypnutá. Dokopy teda 3\cdot3=9 možností.
A pre každú z týchto možností existujú 3 možnosti ako zapojiť vrtuľu C. takže ešte 9 \cdot 3=27 možností. (Preto sa nám ich tu nechcelo vypisovať :D.)
No dobre. Máme teda informáciu, že pre 3 vrtule by to teoreticky vedelo fungovať, keďže majú dostatočný počet možných pohybov. Teraz nám už iba stačí nájsť nejaké také tri hodnoty pohonov A, B, C, že to pre ne bude naozaj fungovať a overiť to.
V zadaní sa nás pýtajú, že “Aký môžu mať tieto vrtule pohon?”. To znamená, že stačí nájsť jednu trojicu, ktorá to bude spĺňať. Je teda v tomto bode úplne korektné aj iba skúšať rad za radom trojice, kým nejaká nebude sedieť :D.
My na to ale skúsime ísť trošku systematickejšie.
Začnime rýchlosťou 1. Ak chceme aby vzducholoď vedela ísť rýchlosťou 1, znamená to, že:
- buď bude mať jedna vrtuľa pohon 1
- alebo bude rozdiel pohonov nejakých dvoch vrtúľ 1
Poďme najprv zistiť, či by nemohlo existovať nejaké riešenie pre prvý prípad. Ak ho nájdeme, nemusíme sa tým druhým vôbec zapodievať :)).
Povedzme teda, že hodnota pohonu A=1.
Ako teraz docieliť rýchlosť 2?
Máme viac možností:
- Pridáme vrtuľu s pohonom B=1, takže súčet A+B=2 a máme pokryté rýchlosti 1 a 2.
- Pridáme vrtuľu s pohonom B=2, takže súčet A+B=3 a máme pokryté rýchlosti 1, 2 a 3.
- Pridáme vrtuľu s pohonom B=3, takže súčet A+B=4 a rozdiel (ak A pôjde dozadu) B-A=2. Budeme mať teda pokryté rýchlosti 1, 2, 3 a 4.
Ak je naším cieľom pokryť všetky hodnoty od 1 do 13, očividne sa najviac oplatí dať tam ako druhú vrtuľu B=3.
Postupným skúšaním už jednoducho prídeme na to, že posledná vrtuľa musí mať hodnotu pohonu 9. Je to v zásade podobný postup ako pri hľadaní vrtule s pohonom 3. Skúšame vrtule 4, 5, 6, 7, 8, 9 a zistíme, že 9 sa oplatí najviac, lebo tak vieme pokryť najviac hodnôt. Dokonca všetky, ktoré potrebujeme:
| Finálna rýchlosť | Spôsob, ako ju docieliť |
|---|---|
| 1 | 1 |
| 2 | 3-1 |
| 3 | 3 |
| 4 | 3+1 |
| 5 | 9-3-1 |
| 6 | 9-3 |
| 7 | 9-3+1 |
| 8 | 9-1 |
| 9 | 9 |
| 10 | 9+1 |
| 11 | 9+3-1 |
| 12 | 9+3 |
| 13 | 9+3+1 |
Ak sa vám zdá, že sme si ten pohon 9 na konci akosi “tipli” a neviete kvôli tomu spávať, odporúčam pozrieť si prvý bod zo sekcie poznámok na záver.
Odpoveď: Potrebujeme aspoň 3 vrtule a môžu mať pohon napríklad 1, 3, 9.
Komentár
Väčšina z vás zvládla nájsť správne hodnoty pohonov. Dokonca sa váš postup hľadania do veľkej miery podobal tomu, ako sme to hľadali my.
Avšak, to, že sme hodnoty pohonov hľadali fakt efektívne neznamená, že sa to nedá aj na menej vrtúľ. Bolo treba venovať zvlášť časť riešenia odôvodneniu, že na menej ako 3 to fakt fakt nejde :))
Poznámky na zamyslenie
To, že loď vie ísť rýchlosťami od 1 do 13 dopredu automaticky znamená, že vie ísť rýchlosťami od 1 do 13 aj dozadu (iba vymeníme znamienka - smer jazdy pri každom zo spôsobov vyššie). Preto sa na čísla 1, 3, 9 dalo prísť tak, že ich súčet musí byť presne 13. Inak by 27 možností pohybov skrátka nestačilo. Lebo 13+1+13=27, čo je súšet možných pohybov dopredu, dozadu, a státie (kedy nejde žiadna vrtuľa). Uvedomiť si toto je však pomerne náročné, preto sme sa rozhodli to vo vzorovom riešení uviesť až takto na záver.
Okrem toho, pozornému čitateľovi isto neušlo, že 1, 3, 9 sú postupne zväčšené trojnásobne. To Znamená, že ak by ďalšia vrtuľa mala hodnotu 27, vedeli by sme pokryť všetky rýchlosti od 1 do 40 (1+3+9+27=40). Zároveň je to dôvod, prečo sú 1, 3, 9 jediné pohony, ktoré pri 3 vrtuliach vyhovujú zadaniu.
3. príklad
Zadanie
Mapa je nakreslená na obdĺžnikovej štvorcovej mriežke. Ak preškrtneme jeden riadok a jeden stĺpec, dokopy sme vyškrtli 25 políčok, a na mape ostane počet políčok deliteľný 7. Ďalej (na tej istej mape) vyškrtneme znova niekoľko riadkov a stĺpcov, pričom vyškrtneme 67 políčok. Aké rozmery mala pôvodná mapa? Nájdite všetky možnosti.
Vzorové riešenie
Nazvime si dĺžky strán obdĺžnika a,b. Z obdĺžnika najprv preškrtneme jedno políčko za každý riadok (preškrtnutý stĺpec) a jedno políčko za každý stĺpec (preškrtnutý riadok). Jedno políčko ale preškrtneme dva krát, keďže je aj v riadku aj stĺpci ktorý preškrtávame. Preto odčítané množstvo políčok bude a+ b-1. Zo zadania vieme, že po preškrtnutí riadku a stĺpca odoberieme 25 políčok, teda:
a+b-1 = 25 \\ a+b = 26
Ďalej vieme, že po odčítaní riadku a stĺpca bude počet políčok deliteľný 7. Nazvime si dĺžky strán nového obdĺžnika a_2, b_2, teda
a_2 = a-1 \\
b_2 = b-1 \\
a_2 + b_2 = 26-1-1=24
Zároveň bude mať nový obdĺžnik obsah a_2 \cdot b_2 o ktorom vieme, že má byť deliteľný siedmimi. Keďže 7-ku nevieme vyskladať ako súčin žiadnych dvoch menších prirodzených čísel (7 je prvočíslo), tak aspoň jedno z a_2,b_2 musí byť deliteľné siedmimi. Na násobok 7 a druhé číslo, s ktorým dáva súčet 24 máme tri možnosti: 7+17, 14+10, 21+3.
Zadanie sa pýta len to, ktoré z týchto možností (resp. o 1 väčších v obobch rozmeroch) vyhovujú. Pre každú možnosť preto stačí buď nájsť spôsob ako preškrtnúť 67 políčok, alebo ukázať že sa to nedá.
- 7,17: Z obdĺžnika s obsahom 7\cdot17 = 119 môžeme škrtnúť 3 riadky so 17 políčkami. Spolu ostane obdĺžnik s rozmermi 4\cdot17 a už len vyškrtneme 4 stĺpce dĺžky 4. Dokopy budeme mať vyškrtnutých 3 \cdot 17 + 4 \cdot4 = 67 políčok a teda táto možnosť sedí.
- 14,10: Z obsahu vyškrtneme 67 políčok, čím dostaneme 14 \cdot 10-67=73 políčok. Žiadne rozmery tabuľky však nemôžu vytvoriť 73 políčok, pretože je to prvočílslo (nevieme ho rozdeliť na žiaden iný počet rovnakých stĺpcov ako na 1 \cdot 73, toľko ich však nemáme)
- 21,3: Obdĺžnik by mal obsah 3\cdot21 = 63, čo je menej ako 67 a táto možnosť nesedí.
Odpoveď: Obdĺžnik mohol mať rozmery 8\cdot18, iné možnosti sme vylúčili.
4. príklad
Zadanie
Kód k číselníku je také číslo, ktoré je jedenásť násobkom svojho ciferného súčtu. Nájdite všetky čísla, ktoré môžu byť kódom a ukážte, že žiadne iné nemôžu existovať.
Vzorové riešenie
Odpoveď:
Najskôr sa zamyslíme, koľko cifier môže mať číslo k. Najrozumnejšie je sa zamyslieť, koľko najviac cifier môže mať - ako náhle zistíme túto informáciu, počet možností sa nám mnohonásobne zmenší.
Dobrým začiatkom je si tipnúť - vyskúšať napríklad štvorciferné. Pri ňom platí, že najväčší možný ciferný súčet je 9+9+9+9 = 36 a 36*11 je 396. Toto sa ani zďaleka nepribližuje ku 1000 a preto vieme, že k bude najviac trojciferné. Tu ešte treba spomenúť, že pre všetky väčšie čísla(päťciferné, šesťciferné...) to bude fungovať rovnako, nakoľko 11 násobok ciferného súčtu rastie pomalšie, ako samotné číslo. (Ciferný súčet sa zvýši o 99, kým samotné číslo sa zvýši 10 krát).
Ak je k jednociferné:
Vieme že k musí byť deliteľné 11 (je jedenásť násobkom svojho ciferného súčtu) a jediné takéto jednociferné číslo je 0.
Ak je k dvojciferné:
Keďže k je deliteľné 11, tak môže byť niektoré z čísel 11, 22, 33, 44, 55, 66, 77, 88, 99, ktorých ciferné súčty sú postupne 2, 4, 6, 8, 10, 12, 14, 16, 18. Tu ale môžeme vidieť že ani jedno k nie je jedenásť násobkom svojho ciferného súčtu a teda k nebude dvojciferné.
Ak je k trojciferné:
Rozložíme si číslo ABC na 100*A + 10*B + C. Zo zadania nám vyplýva, že
100*A + 10*B + C = 11*(A+B+C)
Keď si roznásobíme zátvorku, a odčítame pravú stranu od ľavej, dostaneme
89*A - B - 10*C = 0
Prehodíme záporné členy na pravú stranu:
89*A= B + 10*C
Z tohto je očividné, že A môže byť najviac 1, nakoľko pravá strana vie byť najviac 9+90=99. Keby je A 2, tak ľavá strana je 178, a keby je A ešte viac, rozdiel medzi ľavou a pravou stranou by sa len zvyšoval.
Z toho nám vyplýva, že číslo s najväčším ciferným súčtom je 199 ktorého ciferný súčet je 1+ 9 +9 = 19. K je teda najviac ak 19 * 11 = 209.
Zostávajú nám teda čísla 110, 121, 132, 143, 154, 165, 176, 187, 198 a 209 - všetky trojciferné násobky čísla 11 menšie alebo rovné ako 209. Tieto čísla majú ciferné súčty postupne 2, 4, 6, 8, 10, 12, 14, 16, 18 a 11. Aby sme našli správne k, teraz musíme nájsť znova ich jedenásť násobky: 22, 44, 66, 88, 110, 132, 154, 176, 198 a 121. Môžeme si všimnúť že jediné číslo ktoré sa rovná 11 násobku svojho ciferneho súčtu je 198.
Všetky riešenia sú: 0 a 198
5. príklad
Zadanie
Obrazec na stene zobrazoval násobenie pod seba. Písmenká sú rôzne cifry.
| ? | ? | A | |||
| × | ? | ? | |||
| B | C | B | C | ||
| ? | D | E | ? | ||
| F | G | F | G | ? | |
Nájdite číslo ABCDEFG.
Vzorové riešenie
Najprv si označme zvyšné neznáme aby sa nám prehľadnejšie pracovalo. Budeme ich označovať malými písmenami aby sme rozlíšili, že tieto nie sú nutne rôzne od ostatných číslic. Všimnime si, že posledná cifra výsledku musí byť C keďže v tom stĺpci sčítavame len túto jednu cifru.
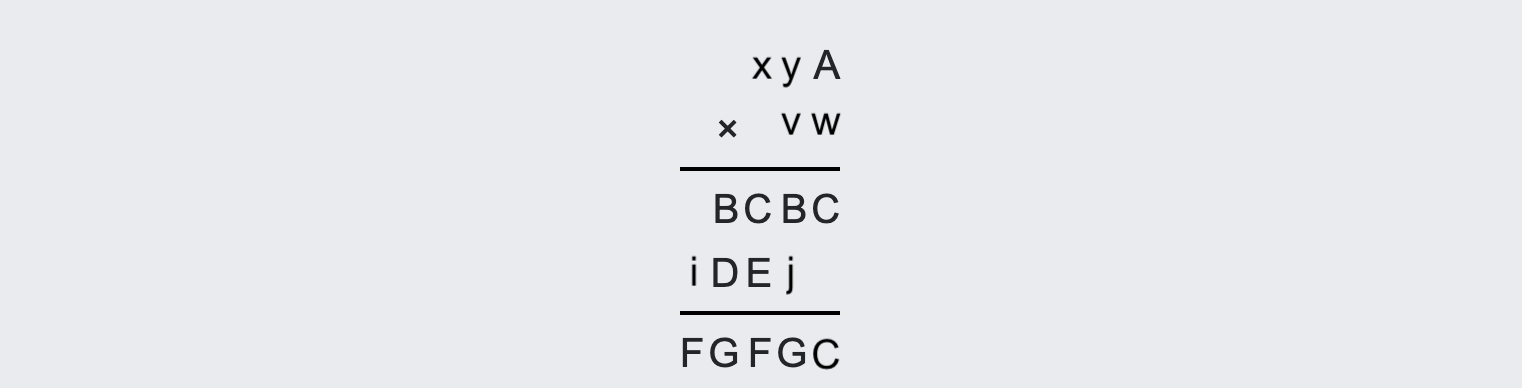
Ešte pre jednoznačnosť, keď napíšeme \overline{OPQ} tak tým myslíme číslo s ciframi O \ P\ Q a podobne pre iné množstvá cifier.
Všimnime, že keďže násobíme pod seba, tak \overline{xyA} \times w=\overline{BCBC} a \overline{xyA} \times v = \overline{iDEj}
Pozrime sa najprv na ten prvý súčin.
\overline{BCBC}=(100+1)\times \overline{BC} =101\times \overline{BC} =\overline{xyA} \times\overline{w}
Po predelení 101 dostávame
\overline{BC}=\frac{\overline{xyA} \times w}{101}
Keďže obe strany musia byť celé čísla a 101 je prvočíslo, tak 101 delí aspoň jedno z w, \overline{xyA}
Ale w je len jednociferné a teda nemôže byť deliteľné 101, preto delí \overline{xyA}
Všimnime si, že všetky trojciferné násobky 101 sú 101, 202, 303, \dots,909, ktoré sú všetky tvaru \overline{A0A} a teda x=A, y=0
Teraz sa pozrime na to druhé násobenie. Vieme niečo povedať o tom ako bude vyzerať niektorý z členov? Vedeli by sme napríklad povedať čomu sa môžu rovnať i,j? Pozrime sa na to druhé násobenie.
\overline{A0A} \times v = \overline{iDEj} \\
101 \times A \times v= \overline{iDEj} \\
Tu si môžeme uvedomiť, že vlastne A,v sú jednociferné čísla a teda ich súčin bude najviac dvojciferný. Povedzme, že ich súčin sa rovná A \times v = \overline{kl}. My síce zatiaľ nevieme, čo to môže byť, ale pozrime sa späť na predchádzajúcu rovnicu.
101 \times A \times v= \overline{iDEj} \\ (100+1) \times \overline{kl}= \overline{iDEj} \\ 100\times \overline{kl} + \overline{kl}= \overline{iDEj} \\ \overline{kl00} + \overline{kl}=\overline{klkl}=\overline{iDEj}
Takto ale môžeme si všimnúť, že máme rovnosť dvoch štvorciferných čísiel, a v jednom sa niektoré cifry rovnajú. Teda konkrétne k=i=E,l=j=D.
Z tohto si ale môžeme všimnúť, že \overline{iDEj}=\overline{EDED}
A teraz sa môžeme konečne pozrieť na sčítanie pod seba.
\overline{BCBC} + 10 \cdot \overline{EFEF}=
\overline{FGFGC} \\
101\cdot \overline{BC} + 101 \times 10 \cdot \overline{EF}=101\cdot\overline{FG}+C
Po predelení 101 a preusporiadaní členov dostaneme:
\overline{BC}+ 10 \cdot \overline{ED} - \overline{FG}=\frac{C}{101}
Teraz si všimnime ale, že ľavá strana je celé číslo, a teda potom aj pravá. No a jediná cifra deliteľná 101 je 0, teda C=0.
Teda \overline{A0A} \times w je číslo končiace 0. Aké máme na to možnosti? No, buď nám končí niektoré z tých čísiel 0, alebo jedno končí 5 a druhé je párne.
Za prvé A \neq 0 lebo vieme zo zadania, že A \neq C a C=0
Za druhé, ak by w=0, tak potom \overline{A0A} \times w=0=\overline{B0B0}, ale 4-ciferné číslo nemôže byť rovné nule. Teda táto možnosť tiež nevyhovuje.
Za tretie ak by A=5 a w bolo párne, tak si stačí uvedomiť, že ľubovoľný násobok 5 končí buď 0 alebo 5, teda v tomto prípade aj \overline{EDED}. Ale už máme že A=5, C=0 a teda sa D nemôže rovnať ani jednej z týchto číslic.
Zostáva teda jediná možnosť, a to w=5, A je párne, z čoho si môžeme uvedomiť, že i D je párne.
Zároveň si môžeme uvedomiť nasledovné:
\overline{A0A} \times 5=0=\overline{B0B0} \\ 505 \times A = 1010 \times B \\ A=2B
Teraz si môžeme spomenúť, že E a F sú zo zadania rôzne cifry. Čo nám to ale hovorí? No všimnime si, že pri sčítaní pod seba nad F máme 0+E, teda jediná možnosť ako môže byť E rôzne od F je, že sme mali prechod cez desiatku. Teda B+D >10 (Rovnosť nastať nemôže lebo potom by sa G=0 ale G má byť rozne od C) a môžeme si napísať, že F=E+1, Zároveň si môžeme uvedomiť, že z tohto vyplýva, že práve jedno z E,F je párne.
Koľko už ale máme tých párnych cifier ktoré majú byť od seba rôzne?, lebo dokopy ich môže byť najviac 5. Máme A,C,D a jedno z E,F. No ale čo ak by bolo i B párne? No potom keďže súčet párnych čísiel je párny, a B,D by boli obe párne tak potom i G. Teraz by sme už ale mali trochu priveľa párnych cifier A,B,C,D,G a jedno z E,F. Teda sporom vieme že B je nepárne.
Keďže B je nepárne a A=2B tak jediné možnosti sú, že A=2, B=1 alebo A=6, B=3
Ak by B=1 ta si všimnime že nemožeme splniť že B+D >10, lebo D je najviac 8
Teda nutne A=6, B=3
Teraz keďže B+D >10, 3+D>10, D>7 a D je párne, tak nutne D=8
B+D=3+8=11 a teda môžeme povedať že G=1
No a teraz sa ešte pozrime späť na súčin 606 \times v= \overline{E8E8}
606 \times v= \overline{E8E8}=101 \times \overline{E8} \\
6 \times v=\overline{E8}
V prvom prípade by sme dostali že E=1, ale to nemôže byť keďže G=1
Zostáva teda v=8, E=4, F=5
A naozaj môžeme si overiť, že toto riešenie už funguje.
606 \times 85=51510
Teda odpoveď je 6308451
6. príklad
Zadanie
Za okrúhlym stolom sedí 420 výprav z rôznych kráľovstiev. Presne polovica kráľovstiev vyslala ako výpravu iba svojho kráľa, a druhá polovica s ním vyslala aj kráľovnú. Bez ohľadu na usadenie výprav, dokázali by sme rozdeliť stôl na dva súvislé neprekrývajúce sa úseky tak, aby každá výprava bola v nejakom úseku a každý úsek obsahoval rovnako veľa ľudí? A čo ak by boli úseky 3? Vedeli by sme to spraviť aj vtedy? Ak áno, nezabudnite ukázať, že to ide vždy.
Vzorové riešenie
Polovica královsitev vyslala jedného človeka a polovica vyslala dvoch ľudí, takže celkovo za stolom sedí 210 + 210 \cdot 2 = 630 ľudí. Rozdeľme si stôl na dva úseky, tak aby v oboch úsekoch bolo 210 výprav, a pozrime sa na počet ľudí v nich – ak jeden úsek obsahuje n ľudí, druhý bude obsahovať 630 - n ľudí. Ak teraz priamku, ktorá tieto dva úseky rozdeľuje, otočíme o jednu výpravu po smere hodinových ručičiek, do oboch úsekov pribudne jedna výprava a jedna ubudne.
Máme niekoľko možností: do úseku pribudne dvojčlenná a odíde jednočlenná – v tomto prípade sa počet ľudí v tomto úseku zväčší o 1, do úseku pribudne jednočlenná a odíde dvojčlenná výprava – v tomto prípade sa počet ľudí v tomto úseku zmenší o 1, do úseku pribudne aj odíde jednočlenná výprava, do úseku pribudne aj odíde dvojčlenná výprava – v oboch týchto prípadoch sa počet ľudí vo výprave nezmení.
Vidíme teda, že počet ľudí sa otočením o jednu výpravu vie zmeniť iba o 1. Zároveň vieme, že ak rozdeľovaciu priamku otočíme 210-krát, úseky sa nám vymenia a náš úsek bude mať 630 - n ľudí. Keďže teda vieme meniť počet ľudí v úseku vždy iba o 1, musel náš úsek niekedy v procese otáčania nadobudnúť všetky hodnoty medzi n a 630-n, a teda aj hodnotu 315, čo je presne polovica. Ak počet ľudí v jednom úseku je presne polovica, v druhom bude počet rovnaký, čiže vždy bude existovať také rozdelenie, v ktorom budú mať oba úseky rovnako veľa ľudí.
Pozrime sa teraz na prípad, kedy sú úseky tri. V každom úseku teraz musí byť 210 ľudí. Ak sú výpravy za stolom rozdelené tak, že niekde sedí jedna výprava s veľkosťou 1 a na oboch stranách okolo nej je 105 výprav s hodnotou 2. Úsek, v ktorom bude táto osamelá jednotka, musí mať párny súčet (210), teda musí obsahovať ešte aspoň jednu jednotku. Medzi najbližšou jednotkou však je 105 výprav veľkosti 2, takže úsek musí obsahovať aj tie. V takom prípade ale bude počet ľudí v ňom aspoň 105\cdot 2+1= 211 a to už je priveľa. Ak máme tri úseky, rozdelenie, kde budú všetky mať rovnakú hodnotu teda neexistuje.
7. príklad
Zadanie
Majme zariadenie v tvare trojuholníka ABC, nech D, E sú na strane BC tak, že |BD| = |DE| = |EC|, nech F je stred CA a nech G je na strane AB tak, že 2|BG| = |GA|. Predpokladajme, že uhol \sphericalangle BGE je pravý. Nech P je priesečník DF s AB. Nech veľkosť AP je 8 a obsah ADF je 4. Nájdite veľkosť GE.
Vzorové riešenie
Zo začiatku sa vždy zíde si obrázok nakresliť:

Všimnime si, že bod E je v \frac{2}{3} strany BC, teda výška od úsečky AB bodu E je tiež \frac{2}{3} výšky bodu C od AB, resp. \frac{2}{3} výšky trojuholníku ABC na stranu AB. Keďže uhol \angle BGE je pravý, úsečka GE je práve výška bodu E od AB. Označíme si v výšku \triangle ABC na stranu AB. Teraz zostáva už len ju nájsť.
Keďže bod F je stred úsečky AC, tak vieme, že výška tohto bodu od AB je \frac{1}{2}v. Teda výška trojuholníku APF na stranu AP je \frac{1}{2}v. Keďže \left|AP\right| = 8, môžem zistiť obsah \triangle APF:
S_{APF}=\frac{\frac{1}{2}v \cdot 8}{2}= 2v
Viem teraz zistiť aj obsah \triangle APD, jednoducho tak, že odčítam známy obsah \triangle ADF od S_{APF}:
S_{APD}=S_{APF} - S_{APD}= 2v - 4.
Všimnime si však, že zároveň výška bodu D od úsečky AP, resp. výška \triangle APD na stranu AP je \frac{1}{3}v, keďže D je v tretine BC pri B. Teda si vieme vyjadriť S_{APD} tiež pomocou tejto výšky a dĺžky strany AP:
S_{APD}=\frac{\frac{1}{3}v \cdot 8}{2} = \frac{4}{3}v .
Máme dva rôzne spôsoby, ako si vyjadriť S_{APD}. Tak si ich dajme do rovnosti.
2v - 4 = \frac{4}{3}v .
6v - 12 = 4v .
2v = 12 .
v = 6 .
Takže už vieme výšku trojuholníku APD. Keďže vieme, že dĺžka \left|GE\right| je práve \frac{2}{3} z v, vieme ju teraz už jednoducho vypočítať
\left|GE\right| = \frac{2}{3}v = \frac{2}{3}6 = 4 .
Odpoveď: \left|GE\right|=4
8. príklad
Zadanie
420 výprav z rôznych krajín sedí za okrúhlym stolom. Úlohou je každej výprave priradiť číslo v poradovníku (od 1 do 420, každé práve raz), avšak s jednou podmienkou. Ak tri výpravy s číslami A, B, C sedia vedľa seba (obsadzujú 3 miesta vedľa seba za stolom v poradí tak, že B je medzi A a C), musí platiť že (A + C) je deliteľné B+1. Je možné s touto podmienkou rozdeliť čísla?
Vzorové riešenie
Pozrime sa na číslo B. V číslach od 1 po 420 sú zaručene nejaké nepárne čísla, takže určite vieme nájsť číslo B, ktoré bude nepárne. B+1 bude párne. A+C bude teda musieť byť násobok párneho čísla a ten bude vždy párny. Párny súčet dostaneme len sčítaním dvoch čísel s rovnakou paritou, teda p + p alebo n + n. Každé nepárne číslo teda musí mať oboch susedov rovnakej parity.
Ak obkolesíme prvé nepárne číslo dvomi nepárnymi, teda máme nnn, číslo naľavo aj napravo už má jedného suseda - nepárne číslo. Ich druhý sused musí taktiež byť nepárny. Týmto spôsobom by sme dostali reťazec iba nepárnych čísel, lenže v číslach od 1 po 420 sú aj párne čísla. Žiadne nepárne číslo teda nebude obkolesené nepárnymi.
Nepárne čísla teda určite musíme obkolesiť párnymi. Keďže máme rovnako veľa párnych aj nepárnych čísel, musia sa nam v reťazci striedať (pnpnpn).
Teraz si zoberme číslo 420 ako číslo B, čiže B+1=421. 420 je párne, bude teda obkolesené dvomi nepárnymi. Dve nepárne čísla budú mať určite párny súčet, teda budú musieť byť párnym násobkom 421. Taký najmenší je 842 (421\times2), lenže aj dve najväčšie nepárne čísla, 419 a 417, majú súčet len 836. To je žiaľ primálo.
Odpoveď: Čísla nevieme zoradiť bez porušenia podmienky v zadaní.
9. príklad
Zadanie
V špeciálnej hre o mincu hodíme mincou 100 krát. Prvý hod je určite hlava, a druhý hod je určite znak. Každý nasledujúci hod funguje nasledovne. Ak sme už doteraz hodili A hláv a B znakov, tak pravdepodobnosť, že v tomto hode hodíme hlavu je \frac{A}{A+B}. Naopak, šanca že hodíme znak je \frac{B}{A+B}. Aká je pravdepodobnosť, že zo 100 hodov padne v práve 50 hlava?
Vzorové riešenie
Keďže mincu hádžeme opakovane, tak pravdepodobnosti jednotlivých hodov budeme násobiť. Poďme sa pozrieť ako bude vyzerať pravdepodobnosť na hodenie 4 hláv z 5 hodov.
Prvý hod je určite hlava (pravdepodobnosť je 1), druhý hod je určite znak (pravdepodobnosť je 1), tretí hod je hlava s pravdepodobnosťou \frac{1}{2}, štvrtý hod je hlava s pravdepodobnosťou \frac{2}{3} a piaty hod je hlava s pravdepodobnosťou \frac{3}{4}. Výsledná pravdepodobnosť je 1 \cdot 1 \cdot \frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} = \frac{1 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 4} = \frac{1}{4}.
Môžeme si všimnúť 3 veci. Prvá dva hody sú dané, takže neovplyvnia výslednú pravdepodobnosť (po zvyšok riešenia ich nebudem písať). V menovateli sa objavia všetky čísla medzi 2 a \text{počet hodov} - 1, inak povedané (\text{počet hodov}-1)!. V čitateli sa objavia všetky čísla medzi 1 a \text{počet hláv}-1 a medzi 1 a \text{počet znakov}-1, inak povedané (\text{počet hláv}-1)! a (\text{počet znakov}-1)!.
Poďme teraz vypočítať pravdepodobnosť, že padne hlava, znak, 49 hláv a 49 znakov v tomto poradí. Podľa odseku vyššie bude vyzerať nasledovne: \dfrac{49!\cdot49!}{99!}.
Teraz si treba uvedomiť, že toto je pravdepodobnosť pre toto konkrétne poradie a zároveň všetky ostatné možnosti ako mohlo tých 98 hodov dopadnúť. Teraz nám ostáva túto pravdepodobnosť vynásobiť počtom možností ako hodiť 49 hláv a 49 znakov. Môžeme si všimnúť, že každá možnosť je určená tým, na ktorých miestach sa nachádzajú hlavy. Takže chceme počet možností ako vybrať 49miest z 98. To vieme vypočítať ako kombinačné číslo \dbinom{98}{49}=\dfrac{98!}{49!\cdot(98-49)!}=\dfrac{98!}{49!\cdot49!}.
Nakoniec už iba vynásobíme \dfrac{49!\cdot49!}{99!}\cdot\dfrac{98!}{49!\cdot49!}=\dfrac{98!}{99!}=\dfrac{1}{99}.
Odpoveď: Pravdepodobnosť, že zo 100 hodov padne 50 hláv je \dfrac{1}{99}.
10. príklad
Zadanie
Chlapci chcú zvnútra vystužiť kocku pomocou kovových trámov. Kocka má rozmery 1000\times1000\times1000, teda vnútro sa skladá z 1000^3 prázdnych kociek vzduchu. Trám má rozmery 1000\times1\times1, a do kocky ho vieme vložiť iba celý tak, aby zaberal presne 1000 kociek vzduchu. Pre správne vystuženú kocku musia platiť nasledovné podmienky:
- Každá stena trámu musí susediť buď so stenou veľkej kocky, alebo s iným trámom. Inými slovami, nemôže existovať taká stena trámu, ktorá celá susedí so vzduchom
- Do kocky musíme vložiť aspoň jeden trám
- Trámy sa nemôžu ohýbať ani prekrývať
Koľko najmenej trámov je potrebných na správne vystuženú kocku?
Vzorové riešenie
Skúsme ukladať trámy tak, aby vyhovovali podmienke. Dobrý začiatok môže byť uložiť trám do rohu. Potom môžeme oň oprieť kolmo otočený trám. Ešte ho treba podoprieť z jednej strany, tak spravme dva v jednom a oprime jednu stranu prvého aj druhého trámu tretím, kolmým na oba: 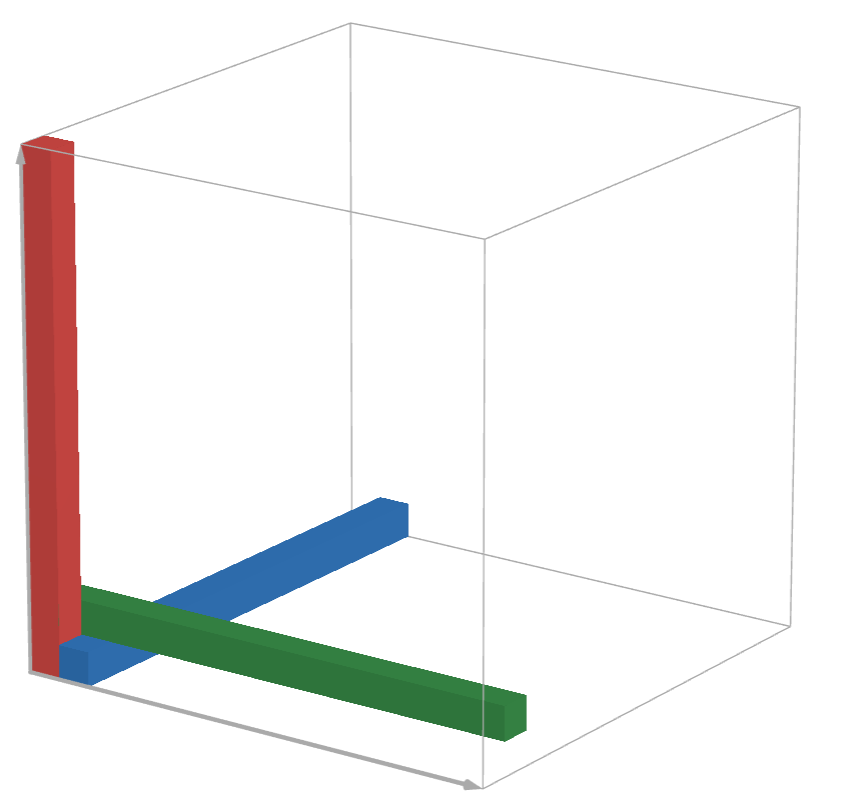 Môžeme pokračovať v ukladaní trámov vždy tak, aby sme tým podopreli dva ďalšie trámy (chceme predsa všetky podoprieť, tak znie ako dobrý nápad skúsiť ich vždy podoprieť čo najviac naraz). Postupne tak dostaneme takéto vystuženie:
Môžeme pokračovať v ukladaní trámov vždy tak, aby sme tým podopreli dva ďalšie trámy (chceme predsa všetky podoprieť, tak znie ako dobrý nápad skúsiť ich vždy podoprieť čo najviac naraz). Postupne tak dostaneme takéto vystuženie:
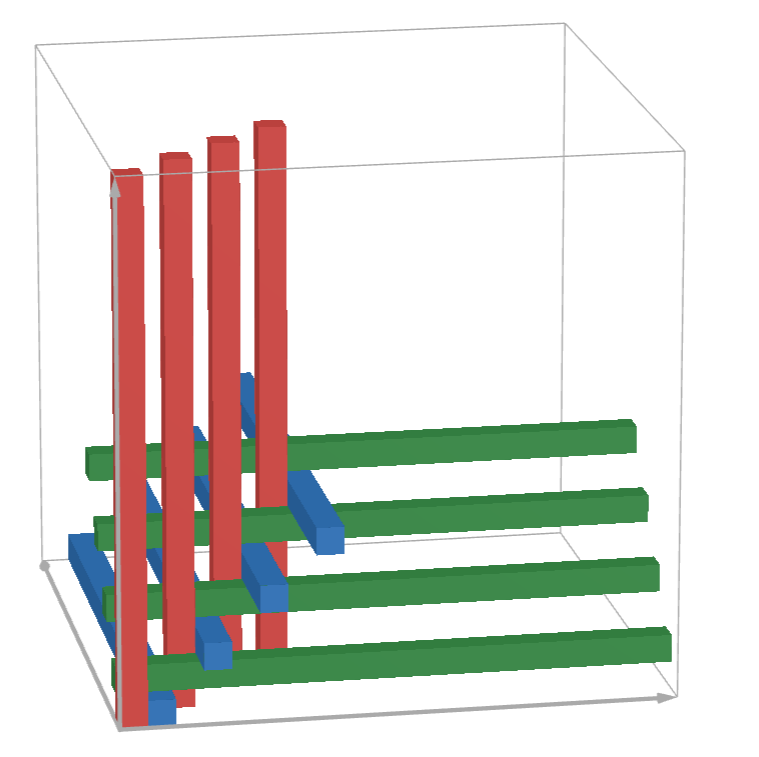
 Toto vystuženie využíva 500 trámov v každom z troch smerov, teda dokopy 1\ 500 trámov.
Toto vystuženie využíva 500 trámov v každom z troch smerov, teda dokopy 1\ 500 trámov.Poďme sa teraz zamyslieť nad tým, či môže existovať lepšie vystuženie kocky. Ukáže sa, že neexistuje. Vo vašich riešeniach ste to ukazovali rôznymi správnymi spôsobmi, tu uvediem jeden, ktorý sa mi zdal veľmi pekný:
Môžeme si všimnúť, že v tomto rozložení trámov je v každej vrstve kocky (1\ 000 \times 1\ 000 \times 1 reze hociktorým z hlavných smerov) jeden trám. Skúsme teda dokázať, že to tak musí byť vždy. Budeme to dokazovať sporom.
Pre spor teda predpokladajme, že existuje vrstva, v ktorej žiadny trám nie je (môže ju nejaký pretínať, ale nie je celý v nej). Potom ani vo vedľajšej vrstve nemôže byť žiadny trám, lebo by ho zo strany, ktorá susedí s predošlou vrstvou, nemalo čo podopierať. Takisto potom nemôže byť žiadny trám ani v nasledujúcej vrstve, ani v tej potom... ani v žiadnej vrstve rovnobežnej s tou pôvodnou.
To znamená, že v kocke môžu byť len trámy kolmé na pôvodnú vrstvu. Každý iný trám totiž leží v nejakej rovnobežnej vrstve.
Ale jediný spôsob ako vystužiť kocku iba takými trámami je, že nimi bude celá vyplnená. Na to ale treba veľmi veľa (1\ 000 \times 1\ 000 = 1\ 000\ 000) trámov a teda to nebude dobré vystuženie.
Ukázali sme teda, že každé rozumné vystuženie bude mať v každej vrstve nejaký trám. Kocka má 1\ 000 vrstiev v každom z troch smerov, teda dokopy 3\ 000 vrstiev. Každý trám je v dvoch vrstvách kolmých na seba. Preto musí byť najmenej \frac{3\ 000}{2} = 1\ 500 trámov (každý "naplní" dve vrstvy a treba ich naplniť 3\ 000).
Preto naše vystuženie je najlepšie.
