Zadania 1. letného kola - Ahojte Rieškari, je začiatok februára a práve sa nám na stránke zjavilo prvé letné kolo. Ak si predtým ešte neriešil Riešky a zaujíma ťa ako na príklady, tak určite mrkni … Prejsť na článok
×5. príklad - Vzorové riešenie
Zadanie
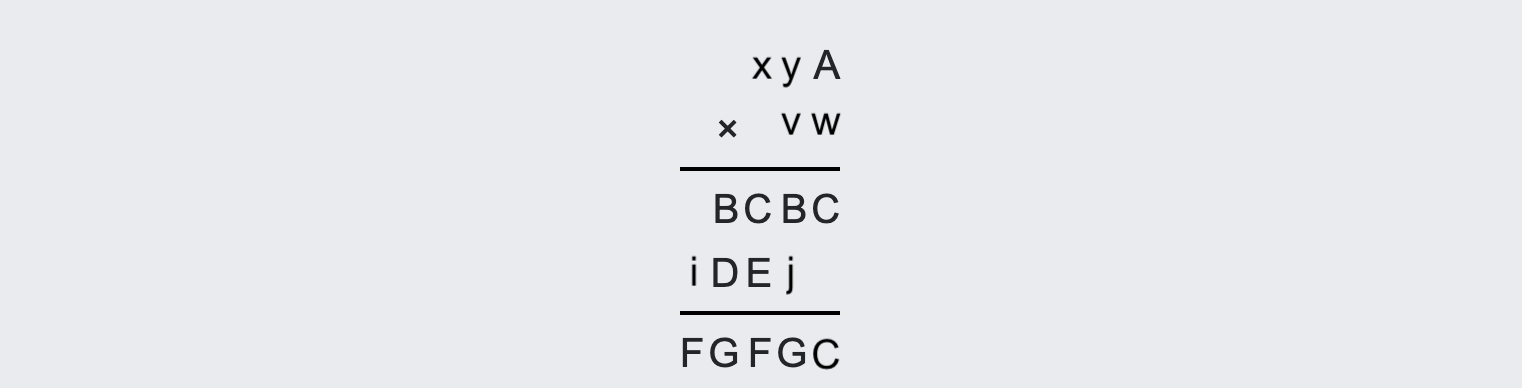
Obrazec na stene zobrazoval násobenie pod seba. Písmenká sú rôzne cifry.
| ? | ? | A | |||
| × | ? | ? | |||
| B | C | B | C | ||
| ? | D | E | ? | ||
| F | G | F | G | ? | |
Nájdite číslo ABCDEFG.
Vzorové riešenie
Najprv si označme zvyšné neznáme aby sa nám prehľadnejšie pracovalo. Budeme ich označovať malými písmenami aby sme rozlíšili, že tieto nie sú nutne rôzne od ostatných číslic. Všimnime si, že posledná cifra výsledku musí byť C keďže v tom stĺpci sčítavame len túto jednu cifru.
Ešte pre jednoznačnosť, keď napíšeme \overline{OPQ} tak tým myslíme číslo s ciframi O \ P\ Q a podobne pre iné množstvá cifier.
Všimnime, že keďže násobíme pod seba, tak \overline{xyA} \times w=\overline{BCBC} a \overline{xyA} \times v = \overline{iDEj}
Pozrime sa najprv na ten prvý súčin.
\overline{BCBC}=(100+1)\times \overline{BC} =101\times \overline{BC} =\overline{xyA} \times\overline{w}
Po predelení 101 dostávame
\overline{BC}=\frac{\overline{xyA} \times w}{101}
Keďže obe strany musia byť celé čísla a 101 je prvočíslo, tak 101 delí aspoň jedno z w, \overline{xyA}
Ale w je len jednociferné a teda nemôže byť deliteľné 101, preto delí \overline{xyA}
Všimnime si, že všetky trojciferné násobky 101 sú 101, 202, 303, \dots,909, ktoré sú všetky tvaru \overline{A0A} a teda x=A, y=0
Teraz sa pozrime na to druhé násobenie. Vieme niečo povedať o tom ako bude vyzerať niektorý z členov? Vedeli by sme napríklad povedať čomu sa môžu rovnať i,j? Pozrime sa na to druhé násobenie.
\overline{A0A} \times v = \overline{iDEj} \\
101 \times A \times v= \overline{iDEj} \\
Tu si môžeme uvedomiť, že vlastne A,v sú jednociferné čísla a teda ich súčin bude najviac dvojciferný. Povedzme, že ich súčin sa rovná A \times v = \overline{kl}. My síce zatiaľ nevieme, čo to môže byť, ale pozrime sa späť na predchádzajúcu rovnicu.
101 \times A \times v= \overline{iDEj} \\ (100+1) \times \overline{kl}= \overline{iDEj} \\ 100\times \overline{kl} + \overline{kl}= \overline{iDEj} \\ \overline{kl00} + \overline{kl}=\overline{klkl}=\overline{iDEj}
Takto ale môžeme si všimnúť, že máme rovnosť dvoch štvorciferných čísiel, a v jednom sa niektoré cifry rovnajú. Teda konkrétne k=i=E,l=j=D.
Z tohto si ale môžeme všimnúť, že \overline{iDEj}=\overline{EDED}
A teraz sa môžeme konečne pozrieť na sčítanie pod seba.
\overline{BCBC} + 10 \cdot \overline{EFEF}=
\overline{FGFGC} \\
101\cdot \overline{BC} + 101 \times 10 \cdot \overline{EF}=101\cdot\overline{FG}+C
Po predelení 101 a preusporiadaní členov dostaneme:
\overline{BC}+ 10 \cdot \overline{ED} - \overline{FG}=\frac{C}{101}
Teraz si všimnime ale, že ľavá strana je celé číslo, a teda potom aj pravá. No a jediná cifra deliteľná 101 je 0, teda C=0.
Teda \overline{A0A} \times w je číslo končiace 0. Aké máme na to možnosti? No, buď nám končí niektoré z tých čísiel 0, alebo jedno končí 5 a druhé je párne.
Za prvé A \neq 0 lebo vieme zo zadania, že A \neq C a C=0
Za druhé, ak by w=0, tak potom \overline{A0A} \times w=0=\overline{B0B0}, ale 4-ciferné číslo nemôže byť rovné nule. Teda táto možnosť tiež nevyhovuje.
Za tretie ak by A=5 a w bolo párne, tak si stačí uvedomiť, že ľubovoľný násobok 5 končí buď 0 alebo 5, teda v tomto prípade aj \overline{EDED}. Ale už máme že A=5, C=0 a teda sa D nemôže rovnať ani jednej z týchto číslic.
Zostáva teda jediná možnosť, a to w=5, A je párne, z čoho si môžeme uvedomiť, že i D je párne.
Zároveň si môžeme uvedomiť nasledovné:
\overline{A0A} \times 5=0=\overline{B0B0} \\ 505 \times A = 1010 \times B \\ A=2B
Teraz si môžeme spomenúť, že E a F sú zo zadania rôzne cifry. Čo nám to ale hovorí? No všimnime si, že pri sčítaní pod seba nad F máme 0+E, teda jediná možnosť ako môže byť E rôzne od F je, že sme mali prechod cez desiatku. Teda B+D >10 (Rovnosť nastať nemôže lebo potom by sa G=0 ale G má byť rozne od C) a môžeme si napísať, že F=E+1, Zároveň si môžeme uvedomiť, že z tohto vyplýva, že práve jedno z E,F je párne.
Koľko už ale máme tých párnych cifier ktoré majú byť od seba rôzne?, lebo dokopy ich môže byť najviac 5. Máme A,C,D a jedno z E,F. No ale čo ak by bolo i B párne? No potom keďže súčet párnych čísiel je párny, a B,D by boli obe párne tak potom i G. Teraz by sme už ale mali trochu priveľa párnych cifier A,B,C,D,G a jedno z E,F. Teda sporom vieme že B je nepárne.
Keďže B je nepárne a A=2B tak jediné možnosti sú, že A=2, B=1 alebo A=6, B=3
Ak by B=1 ta si všimnime že nemožeme splniť že B+D >10, lebo D je najviac 8
Teda nutne A=6, B=3
Teraz keďže B+D >10, 3+D>10, D>7 a D je párne, tak nutne D=8
B+D=3+8=11 a teda môžeme povedať že G=1
No a teraz sa ešte pozrime späť na súčin 606 \times v= \overline{E8E8}
606 \times v= \overline{E8E8}=101 \times \overline{E8} \\
6 \times v=\overline{E8}
V prvom prípade by sme dostali že E=1, ale to nemôže byť keďže G=1
Zostáva teda v=8, E=4, F=5
A naozaj môžeme si overiť, že toto riešenie už funguje.
606 \times 85=51510
Teda odpoveď je 6308451
