Zverejnili sme 3. kolo - Milí riešitelia, Na stránke sme už zverejnili posledné kolo tejto série, jeho zadania môžete nájsť aj na tomto odkaze. Termín odovzdania je 4.12., tak hor sa na to, a držíme … Prejsť na článok
×10. príklad - Vzorové riešenie
Zadanie
Chlapci chcú zvnútra vystužiť kocku pomocou kovových trámov. Kocka má rozmery 1000\times1000\times1000, teda vnútro sa skladá z 1000^3 prázdnych kociek vzduchu. Trám má rozmery 1000\times1\times1, a do kocky ho vieme vložiť iba celý tak, aby zaberal presne 1000 kociek vzduchu. Pre správne vystuženú kocku musia platiť nasledovné podmienky:
- Každá stena trámu musí susediť buď so stenou veľkej kocky, alebo s iným trámom. Inými slovami, nemôže existovať taká stena trámu, ktorá celá susedí so vzduchom
- Do kocky musíme vložiť aspoň jeden trám
- Trámy sa nemôžu ohýbať ani prekrývať
Koľko najmenej trámov je potrebných na správne vystuženú kocku?
Vzorové riešenie
Skúsme ukladať trámy tak, aby vyhovovali podmienke. Dobrý začiatok môže byť uložiť trám do rohu. Potom môžeme oň oprieť kolmo otočený trám. Ešte ho treba podoprieť z jednej strany, tak spravme dva v jednom a oprime jednu stranu prvého aj druhého trámu tretím, kolmým na oba: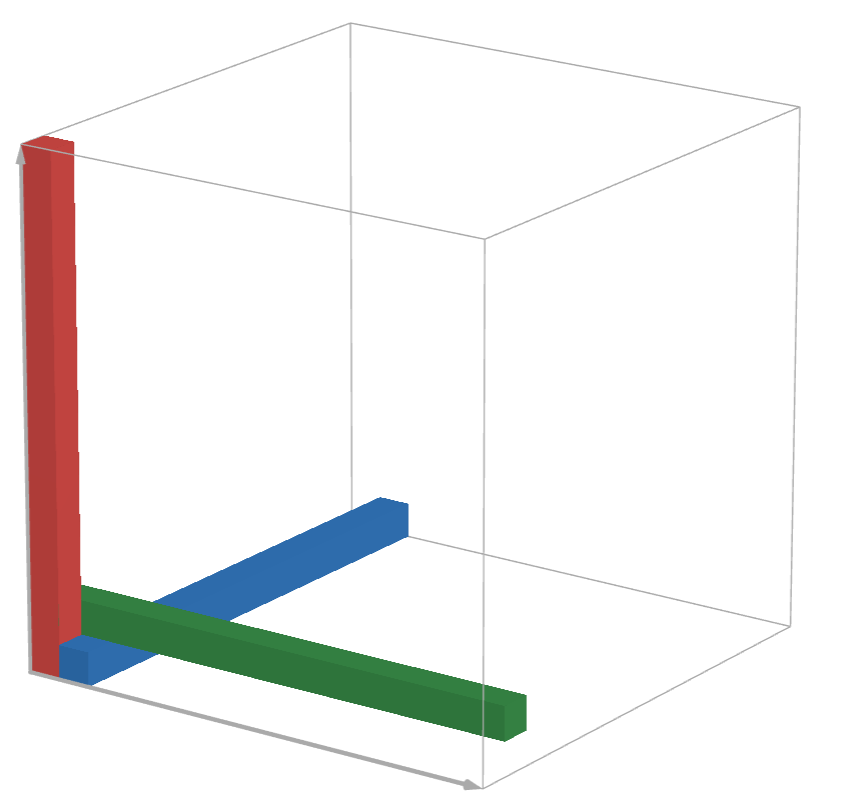 
Môžeme pokračovať v ukladaní trámov vždy tak, aby sme tým podopreli dva ďalšie trámy (chceme predsa všetky podoprieť, tak znie ako dobrý nápad skúsiť ich vždy podoprieť čo najviac naraz). Postupne tak dostaneme takéto vystuženie:
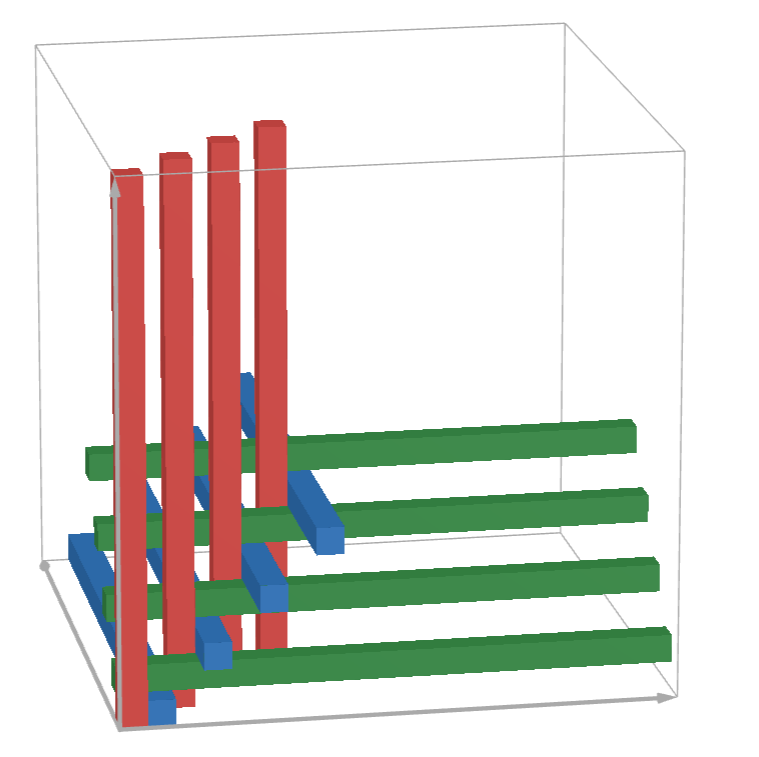
Toto vystuženie využíva 500 trámov v každom z troch smerov, teda dokopy 1\ 500 trámov.Poďme sa teraz zamyslieť nad tým, či môže existovať lepšie vystuženie kocky. Ukáže sa, že neexistuje. Vo vašich riešeniach ste to ukazovali rôznymi správnymi spôsobmi, tu uvediem jeden, ktorý sa mi zdal veľmi pekný:
Môžeme si všimnúť, že v tomto rozložení trámov je v každej vrstve kocky (1\ 000 \times 1\ 000 \times 1 reze hociktorým z hlavných smerov) jeden trám. Skúsme teda dokázať, že to tak musí byť vždy. Budeme to dokazovať sporom.
Pre spor teda predpokladajme, že existuje vrstva, v ktorej žiadny trám nie je (môže ju nejaký pretínať, ale nie je celý v nej). Potom ani vo vedľajšej vrstve nemôže byť žiadny trám, lebo by ho zo strany, ktorá susedí s predošlou vrstvou, nemalo čo podopierať. Takisto potom nemôže byť žiadny trám ani v nasledujúcej vrstve, ani v tej potom... ani v žiadnej vrstve rovnobežnej s tou pôvodnou.
To znamená, že v kocke môžu byť len trámy kolmé na pôvodnú vrstvu. Každý iný trám totiž leží v nejakej rovnobežnej vrstve.
Ale jediný spôsob ako vystužiť kocku iba takými trámami je, že nimi bude celá vyplnená. Na to ale treba veľmi veľa (1\ 000 \times 1\ 000 = 1\ 000\ 000) trámov a teda to nebude dobré vystuženie.
Ukázali sme teda, že každé rozumné vystuženie bude mať v každej vrstve nejaký trám. Kocka má 1\ 000 vrstiev v každom z troch smerov, teda dokopy 3\ 000 vrstiev. Každý trám je v dvoch vrstvách kolmých na seba. Preto musí byť najmenej \frac{3\ 000}{2} = 1\ 500 trámov (každý "naplní" dve vrstvy a treba ich naplniť 3\ 000).
Preto naše vystuženie je najlepšie.