Vzorové riešenia 1. kola

Ak by veľký aj malý motor v jeden deň spotrebovali najviac paliva ako môžu, dokopy by spotrebovali 10 bandasiek paliva (malý motor by spotreboval 3 bandasky a veľký 7 bandasiek). Ak by malý aj veľký motor v jeden deň spotrebovali najmenej paliva ako môžu, dokopy by spotrebovali 5 bandasiek paliva (malý motor by spotreboval 1 bandasku a veľký 4 bandasky).

Vďaka tomuto vieme povedať, že spolu mohli spotrebovať iba také počty bandasiek, ktoré sú aspoň najmenšia spotreba a najviac najväčšia spotreba - teda dokopy mohli spotrebovať 4, 5, 6, 7, 8, 9, 10 bandasiek paliva. 

Vidíme, že mohli spotrebovať spolu najviac 6 rôznych počtov bandasiek. Dní v týždni je však 7, čo je o jeden viac ako možností počtov spotrebovaných bandasiek. Prvých 6 dní v týždni sa teda mohli spotrebovať rôzne počty bandasiek, no siedmy deň sa musel znova spotrebovať rovnaký počet bandasiek ako v nejaký predošlý deň.

Najprv nájdime najväčšie vzdialenosti, ktoré môžu mať dva body, ktoré sa nachádzajú na tom istom útvare z reťaze.

Ak je útvarom:

• kružnica: Najväčšia vzdialenosť 2 bodov na nej je priemer a ten je dvojnásobkom polomeru, takže 2m.
• pravidelný šesťuholník: Pravidelný šesťuholník si vieme rozdeliť na 6 rovnostranných trojuholníkov. Ďalej mu opíšme kružnicu. Keďže pravidelný šesťuholník je symetrický, tak jej stred bude ležať v bode S. Dané trojuholníky sú rovnostranné, takže táto kružnica má polomer 1m. Celý šesťuholník leží vo vnútri tejto kružnice. Preto najväčšia vzdialenosť medzi dvoma bodmi v šesťuholníku je najviac toľko, čo najväčšia vzdialenosť v kružnici, ktorá je 2m. Túto vzdialenosť vieme dosiahnuť napríklad voľbou dvoch protiľahlých vrcholov.

• rovnostranný trojuholník: V rovnostrannom trojuholníku je najväčšia vzdialenosť dvoch bodov dĺžka hrany tohoto trojuholníka a teda 1m.

Rozdelme si našu reťaz na strednú časť E a 4 prívesky A,B,C a D. Zrátajme si ich dĺžky:

• A: Ide o trojuholník, takže dĺžka je 1m.
• B: Ide o kružnicu, takže dĺžka je 2m.
• C: Ide o kružnicu, ktorú vieme predĺžiť ešte o trojuholník, takže dĺžka je 2m+1m=3m
• D: Mohlo by nás lákať povedať, že ide o 4 trojuholníky, ale všimnime si, že trojuholník 9 vie mať najvzdialenejší bod od šesťuholníka 5 vzdialený iba o 2m, lebo je k nemu pripojený trojuholníkom 8. Rovnako pre trojuholník 10. Trojuholníky 8 a 11 môžu byť od seba vzdialenejšie, ale je jasné, že nebudú oba súčasťou najdlšieho predĺženia kotevnej reťaze. Dĺžka je teda 2m.
• E: Predĺženie 2 šesťuholníkov a kružnice je maximálne 2m+2m+2m=6m.

Nakoniec si musíme rozmyslieť ktoré z príveskov a útvarov strednej časti budú v najväčšom predĺžení. Keď sa chvíľku zamyslíme nad možnosťami, tak uvidíme, že najväčšie predĺženie dosiahneme, ak v ňom bude stredná časť a prívesky B a C. Dokopy predĺženie bude 2m + 6m +3m =11m. Natiahnutá reťaz bude vyzerať napr. ako na obrázku.

Odpoveď: Reťaz držiaca kotvu vie mať najviac 11m

Komentár:

Príklad väčšina z vás pekne vyriešila. Stačilo to zdôvodniť menej formálne ako vo vzorovom riešení, ktoré tiež necháva niektoré otázky otvorené. Hlavným cieľom bolo aby ste sa pohrali s priestorovou predstavivosťou a to sa podarilo. K častým problémom patrilo, že ste si neuvedomili, že v ľavej časti reťaze má kružnica väčší priemer, ako je dĺžka strany trojuholníka, poprípade ste nevysvetlili, prečo je vpravo vhodnejšie zvoliť do najdlhšieho rozmeru prívesok C a nie D.

Aby sa nám v riešení rozumne vyjadrovalo, označme si riadky od 1 do 6 zhora dole a stĺpce od A do H zľava doprava. Pričom v stĺpci A a H sú vždy len dva štvorčeky, tie v riadkoch 3 a 4.

Budovy rôznych typov (čísel) sa navzájom neovplyvňujú. (Samozrejme s výnimkou toho, že nemôžu byť na rovnakom políčku.) Oplatí sa teda ísť postupne po typoch budov a zapisovať si, kde môžeme uložiť ďalšie budovy tohto typu. Ktorými budovami však chceme začať? Jednotkovými? Šestkovými? Skúsme sa nad tým trošku zamyslieť, aby sme hlbšie pochopili ako to s tými vzdialenosťami vlastne funguje.

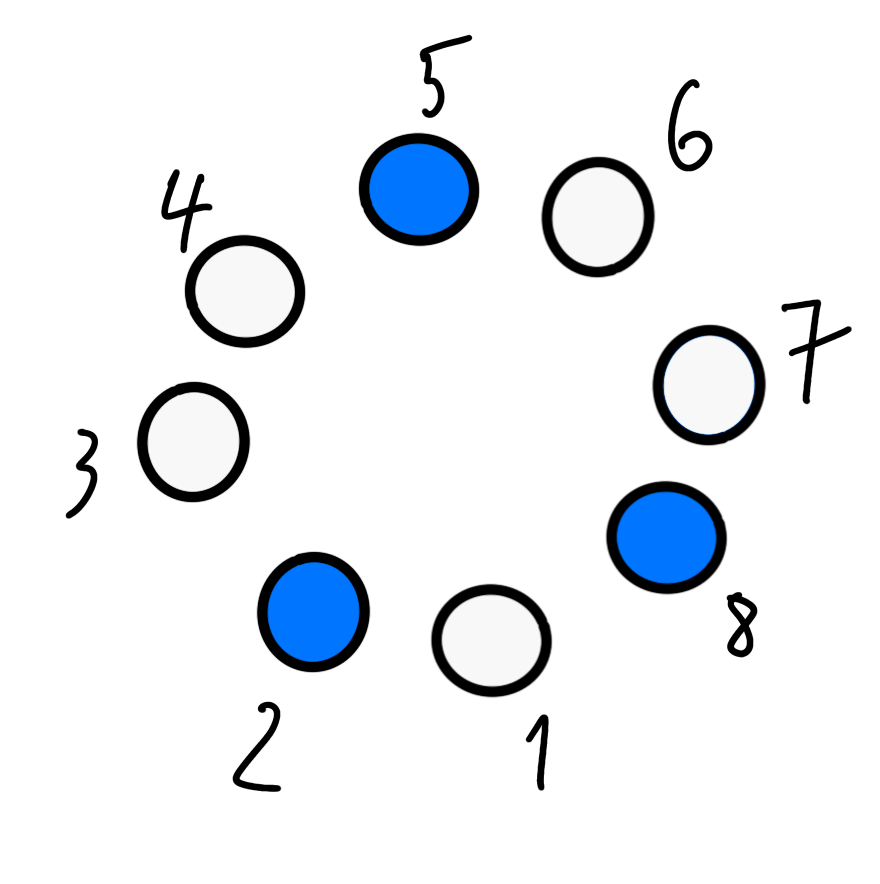
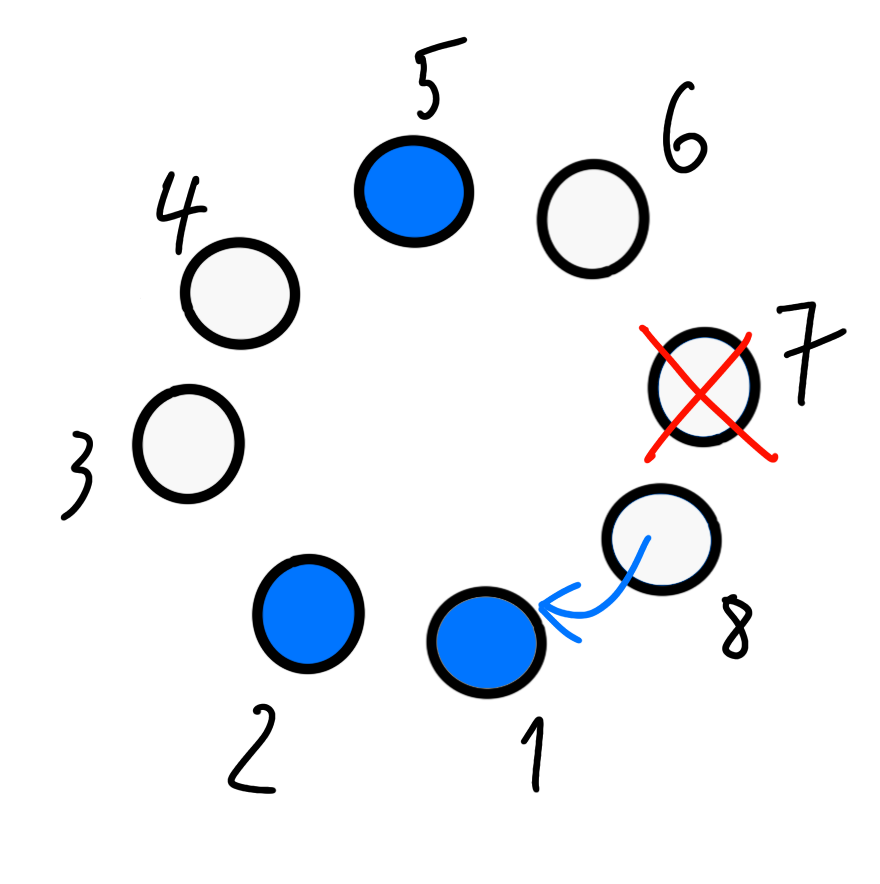
Pozrime sa kde všade by mohli byť budovy rovnakého typu ak už je nejaká budova položená na plániku. Modrou si vždy označíme budovu, ktorá na plániku už položená je. Žltou budú budovy, ktoré k nej môžeme pridať, lebo sú od nej na vzdialenosť N.

Takto to bude vyzerať pre jednotku. Aspoň 2 z tých štyroch žltých budov tam nutne musia byť, aby platilo, že sú od nej vzdialené 1.

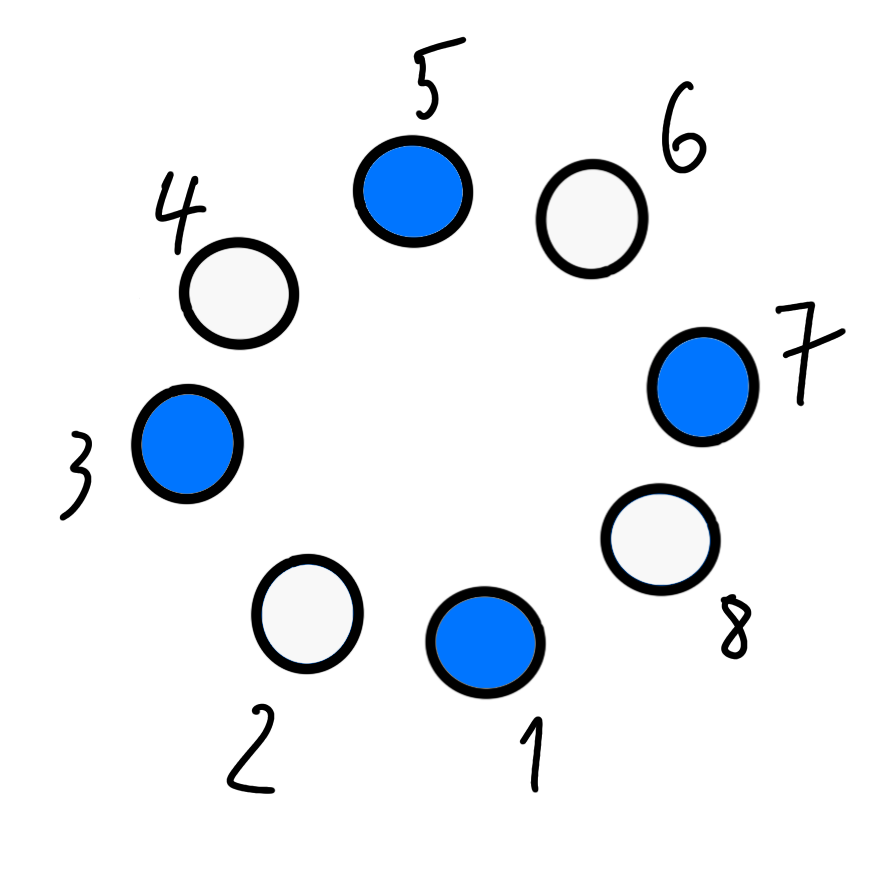
Pre dvojkovú budovu si zase musíme vybrať dve z týchto budov (označených žltou). 

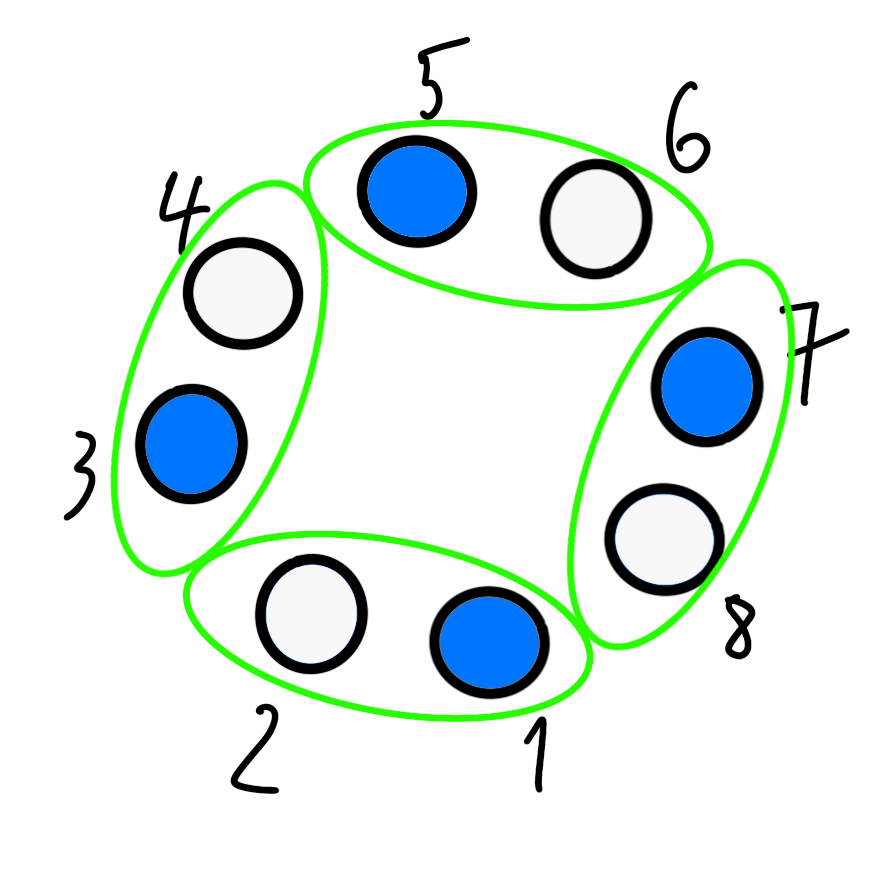
A pre trojky to bude vyzerať takto:

Môžete vidieť, že pre každú z budov sú jej možní parťáci na obvode takého žltého diagonálneho štvorca.

Pre veľké čísla bude veľká časť tohto štvorca ležať mimo tabuľky. Takže napriek tomu, že tých políčok na vyskúšanie je dokopy viac (kedže štvorec je väčší), iba pár z nich sa nám zmestí do tabuľky. Preto nám v skutočnosti bude stačiť vyskúšať menej políčok, na ktorých by mohli byť susedné budovy. To znamená že sa oplatí začať s veľkými číslami. Tak začnime so šestkou.

Od tejto šestkovej budovy na políčku F5 si vyznačme modrou políčka na ktorých môžu byť ďalšie šestkové budovy. A to tak, že bude splnená podmienka, že sú od nej vzdialené N (teda 6). Tieto možnosti sú len tri. (Tu vidíme že sa oplatilo začať šestkou ;).) Na tieto políčka treba položiť dve budovy.

Predstavme si, že dáme šestkovú budovu na 3B. Poďme sa pozrieť na ďalšie políčka kam môžeme dať druhú šestkovú budovu.

Všimnime si, že tieto políčka sú od našej novej budovy vzdialené o menej ako 6. A teda nevieme umiestniť druhú šestkovú budovu pre F5. Zostávajú nám preto tieto dve políčka na naše dve budovy.

Teraz poďme na päťkové budovy. Začnime tou vpravo dole, na políčku G5. Opäť si označme políčka, ktoré sú od päťkovej budovy na mriežke vzdialené 5.

Teraz z nich dajme preč tie políčka, ktoré sú k druhej päťkovej budove na políčku 2B bližšie ako 5. Sú to políčka E2 a C4, zafarbíme si ich na bledočerveno.

Zostali nám dve políčka na dve budovy, čo je presne počet, ktorý potrebujeme.

Zároveň si všimnime, že nám zostali iba políčka vzdialené o 5 od oboch päťkových budov. Teda máme štyri päťkové budovy, a každá má dvoch susedov vzdialených 5. 

Tým máme päťky vyriešené.

Poďme na štvorkové budovy. Začnime štvorkovou budovou na políčku H4. Vyfarbime si políčka, ktoré sú o 4 vzdialené od tejto budovy.

Dajme preč políčka ktoré sú bližšie ako 4 k nejakej ďalšej štvorkovej budove. Konkrétne je také políčko jedno, a to políčko E5.

Ak by budova bola na jednom z troch bledozelených políčok označených nižšie, tak by bola vzdialená 4 od troch štvorkových budov. Konkrétne budov na C1, F6 a H4. Preto na nich budova 4 byť nemôže.

Zostalo nám jedno políčko pre jednu štvorkovú budovu, čo je presne to, čo k budove na H4 potrebujeme.

Teraz si zafarbime políčka vzdialené 4 od budovy na F6. Všimnime si, že tri z nich sme už vylúčili vyššie a na jedno sme už budovu uložili. Máme na teda výber dve políčka: B6 a C5.

Skúsme položiť budovu na políčko B6.

Štvorková budova na B6 potrebuje ešte jednu budovu vzdialenú 4. Vyfarbime políčka vo vzdialenosti 4 od B6.

Políčko E5 je bližšie ku inej štvorke ako 4. Na políčku D4 by bola budova vzdialená N políčok od až 3 budov, čo nám nespĺňa podmienku 2. Políčko C3 je blízko štvorky na C1.

To znamená že na políčku B6 štvorková budova byť nemôže.

Štvorková budova teda musí byť na C5.

Týmto je zároveň splnená podmienka aj pre budovu na C1.

Pokračujme s trojkovými budovami. Pre A3 existujú len dve neobsadené políčka, ktoré sú od nej vzdialené 3. Tak tam určite musia byť trojkové budovy.

B1, ktorú sme práve doplnili, je spojená s jednou budovou na A3 takže pre ňu musíme nájsť ešte jednu budovu. Ak by sme položili budovu na C3 alebo B4 tak by táto budova bola príliš blízko iných trojkových budov. Od políčka D2 existujú až tri trojkové budovy, ktoré od neho majú vzdialenosť 3, čo je v rozpore so zadaním. Preto trojková budova musí byť na políčku E1.

Teraz sa pozrime na G2. K budove na tomto políčku treba nájsť ešte jednu. Z možných políčok, D2 a E3 sú príliš blízko k trojke na E1. Teda jediné možné políčko je F4.

Všetky trojkové budovy majú práve dvoch susedov vzdialených 3 a zároveň sa už nedá umiestniť žiadna ďalšia trojková budova.

Pokračujme s dvojkami. Pre B5 existujú len dve políčka vzdialené o 2. Teda dvojky na týchto políčkach sú jednoznačne dané. 

Dvojka na políčku D5 potrebuje ešte jednu dvojku, a políčko E6 je jediná možnosť.

Dvojka na políčku E5 však tiež potrebuje jednu dvojku. Ak sa pozrieme na políčka, ktoré sú od nej vzdialené o 2, jediná možnosť je políčko E6.

Od dvojky na E6 treba ešte určite dať dvojku aj na G4.

Lenže pri dvojke na G4 máme dve možnosti.

Poďme sa teda radšej presunúť na budovu na C2, niekedy sa oplatí ísť na takéto prípady akosi "z druhého konca" ;). C2 potrebuje ešte jednu dvojku. Jediná možnosť je na E2. Dáme ju teda tam.

Dvojka na E2 potrebuje druhú dvojku. Jediná možnosť je na F3. Tým sme si mimochodom vyriešili aj dvojku na G4.

Takže dvojky by sme mali.

Poďme sa pozrieť na jednotky.

Začnime tou na E4. Máme tri možnosti, kam umiestniť jednotky tak, že od nej budú vzdialené 1, a to políčka E3, D4 a E5. V prípade, že by sme dali jednotku na E5, nevieme tejto jednotke už dať ďalšiu dvojičku.

Takže jednotky musia byť v políčkach E3 a D4, čím máme splnené všetky podmienky pre všetky budovy.

 Odpoveď:

Takže jediné riešenie úlohy je toto:

Začnime tým, že si doplníme označenie pre zvyšné 2 políčka.

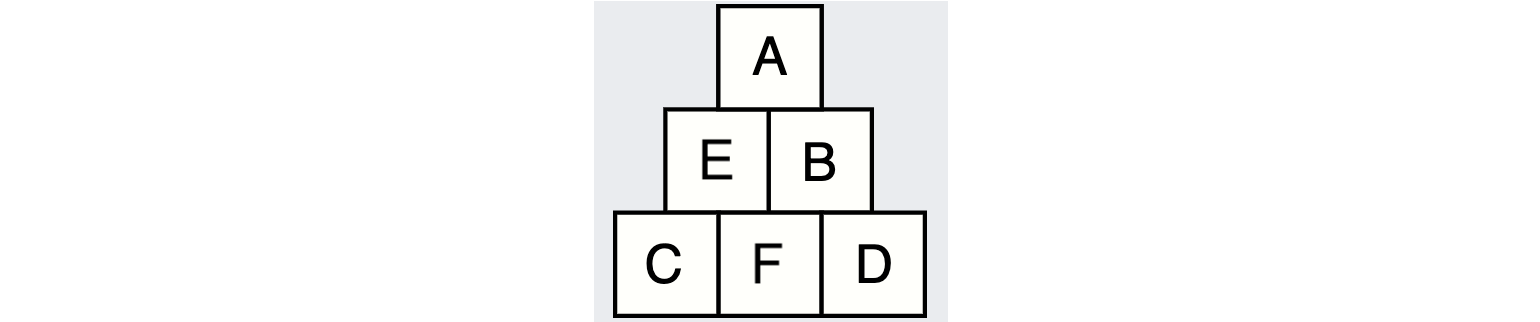
Teraz si potrebujeme uvedomiť dve veci ohľadom zadania:

Po prvé, všetky čísla v pyramíde sú kladné celé. To znamená, že pod každým číslom je len konečne veľa kombinácií, ktorých súčet dáva to číslo. Napríklad: 4=1+3=2+2=3+1
Taktiež to hovorí, že C,F,D sú aspoň 1, z čoho vyplýva, že E,B sú aspoň 2 a A je aspoň 4

Je dôležité si ale uvedomiť, že ak poznáme číslo, nehovorí nám to veľa o číslach nad ním.
Kebyže napríklad B=5, tak jediné čo vieme, je že A ktoré sa rovná E+B, je viac alebo rovné, ako 2+5 (keďže E je aspoň 2). To nám ale nedáva žiadne horné ohraničenie, teda A môže byť hocičo väčšie ako 6, čo už nie je konečne veľa možností.

Po druhé, musíme správne pochopiť výrok Agenta OP. Rozdeľme si ho na jeho dve časti:

Najprv povedal, že nevie akú silu majú všetci agenti.
Keďže pozná sily B a C, tak jediné čo nám to hovorí, je že B\neq2 , pretože kebyže B=2, tak vieme, že F=D=1, a potom vie dopočítať všetky hodnoty. Kebyže je ale B väčšie, tak nemá ako povedať ktorá z možností to bude, lebo C samo o sebe už žiadnu podstatnú informáciu o ostatných nedáva.

Podruhé povedal, že nevie, či to vie Agentka XY dopočítať bez toho aby počula tú vetu.
Toto vie byť veľmi ťažké na spracovanie, preto sa na to pozrime poriadnejšie.

Môžeme sa pozrieť na opak tohto výroku aby sme vedeli ako veci určite nie sú.
Opak by bol: Viem že to nevieš dopočítať bez toho aby si počula túto vetu.

Čo by toto znamenalo? Spomeňme si, že veľkosť čísla obmedzuje veľkosť čísiel pod ním a teda to zužuje na konečné množstvo kombinácií.

Agentka XY pozná A, D. Vieme ale keďže sa jedná o súčkovú pyramídu, tak:

A=E+B=(C+F)+(F+D) \\ A=C+2F+D \\ A-D=C+2F

Keďže C,F\ge1 tak A-D\ge3
Všimnime si, že agentka XY, pozná hodnotu A-D, a že agent OP vie že ju pozná.

Naďalej si všimnime, že keď A-D\leq4, tak v kladných celých číslach, je len jedna možnosť pre hodnoty C,F. 

Konkrétne keď A-D=3 tak C=1, F=1 a keď A-D=4 tak C=2, F=1
Naopak, keď A-D\ge5, tak je už viacero možností na hodnoty C,F. Všimnime si, že kebyže Agent OP vie, že A-D\ge5, tak vie, že Agentka XY nemá ako zistiť všetky čísla sama od seba.

Keďže Agent OP vie C, tak ak by C\ge3 tak, vie, že A-D=C+2F\ge5 a teda vie, že Agentka XY nemá ako zistiť sama od seba čísla. Keďže ale povedal, že nevie či to vie, tak C\le2.

Teda Agentka XY vie, že C\le2 Ako ale zistí, či je to 1 alebo 2?
Pozrime sa znova na rovnicu A-D=C+2F

Keďže 2F je vždy párne, takk by A-D bolo nepárne, tak vie, že C musí byť nepárne.
Podobne, ak by bolo A-D párne, tak i C musí byť párne.

Keďže Agentka XY pozná A-D a teraz už vie, že C je 1 alebo 2, tak už si vie dorátať, ktorá z tých dvoch hodnôt to je.

Teraz už Agentka XY pozná A,C,D a zvyšné už vie dopočítať nasledovne:

A-D=C+2F \ /-C \\ A-C-D=2F \ /:2 \\ F=\frac{A-C-D}{2} \\ E=C+F \\ B=F+D

Zo začiatku je užitočné si obrázok nakresliť:

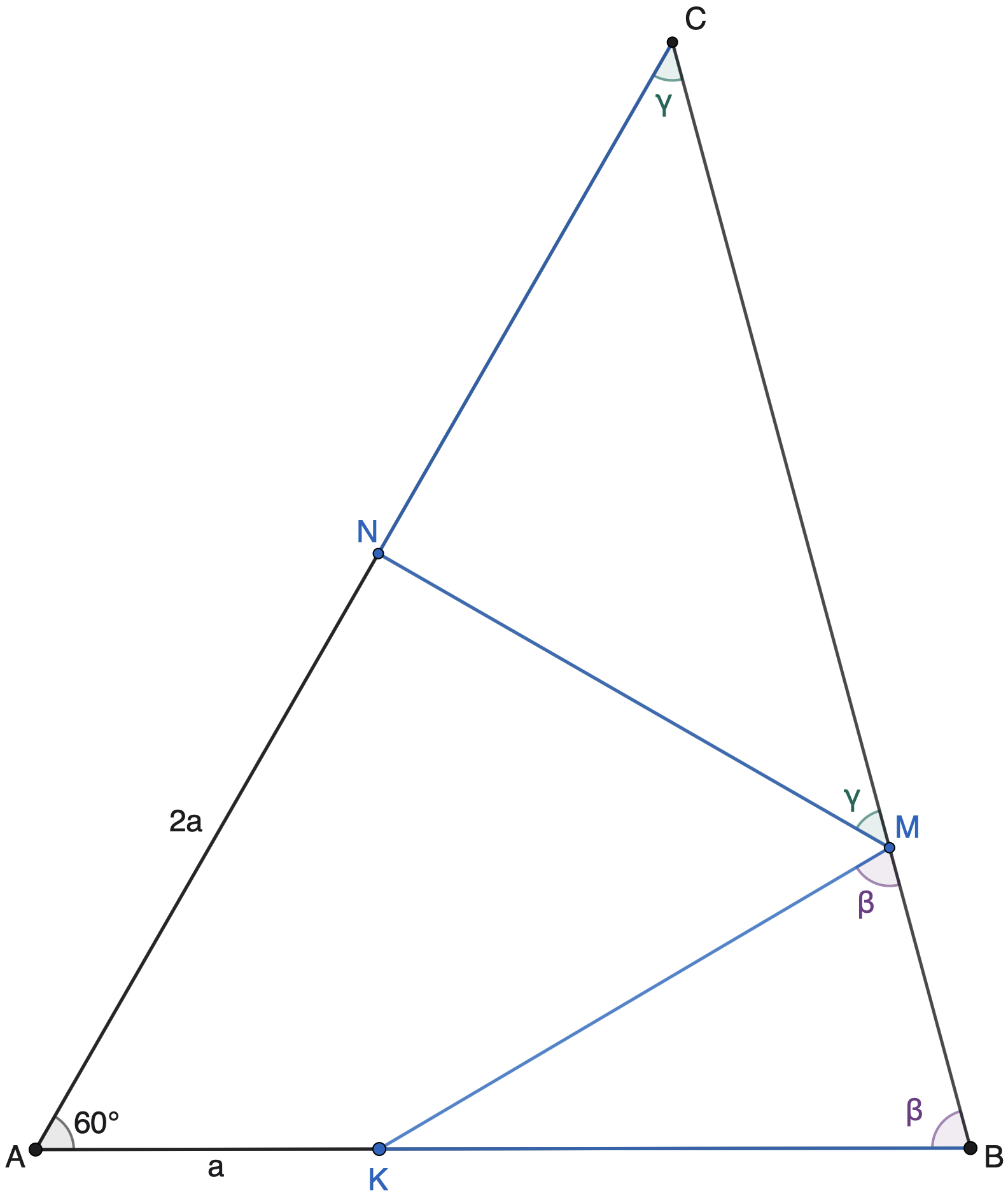
Označíme si veľkosť uhlov v trojuholníku ABC ako \left|\angle ABC \right| = \beta a \left|\angle ACB \right| = \gamma. Všimnime si, že môžeme tiež povedať \left|\angle NMC \right| = \gamma a \left|\angle KMB \right| = \beta, keďže vieme, že \left| BK\right| = \left| KM\right| a \left| MN\right| = \left| NC\right|, teda trojuholníky KBM a NMC sú rovnoramenné, a teda ich uhly pri základniach sú rovnaké.

Pozrime sa teraz na trojuholník AKN. Vieme, že \left|AK\right| je polovica z \left|AN\right|. Môžeme si teraz zvoliť taký bod X na priamke AB, ktorý je od A vzdialený rovnako ako N, alebo teda od bodu K vzdialený rovnako ako bod A, len na opačnej polpriamke. V potstate si chceme "dokresliť" trojuholník AKN na rovnoramenný.

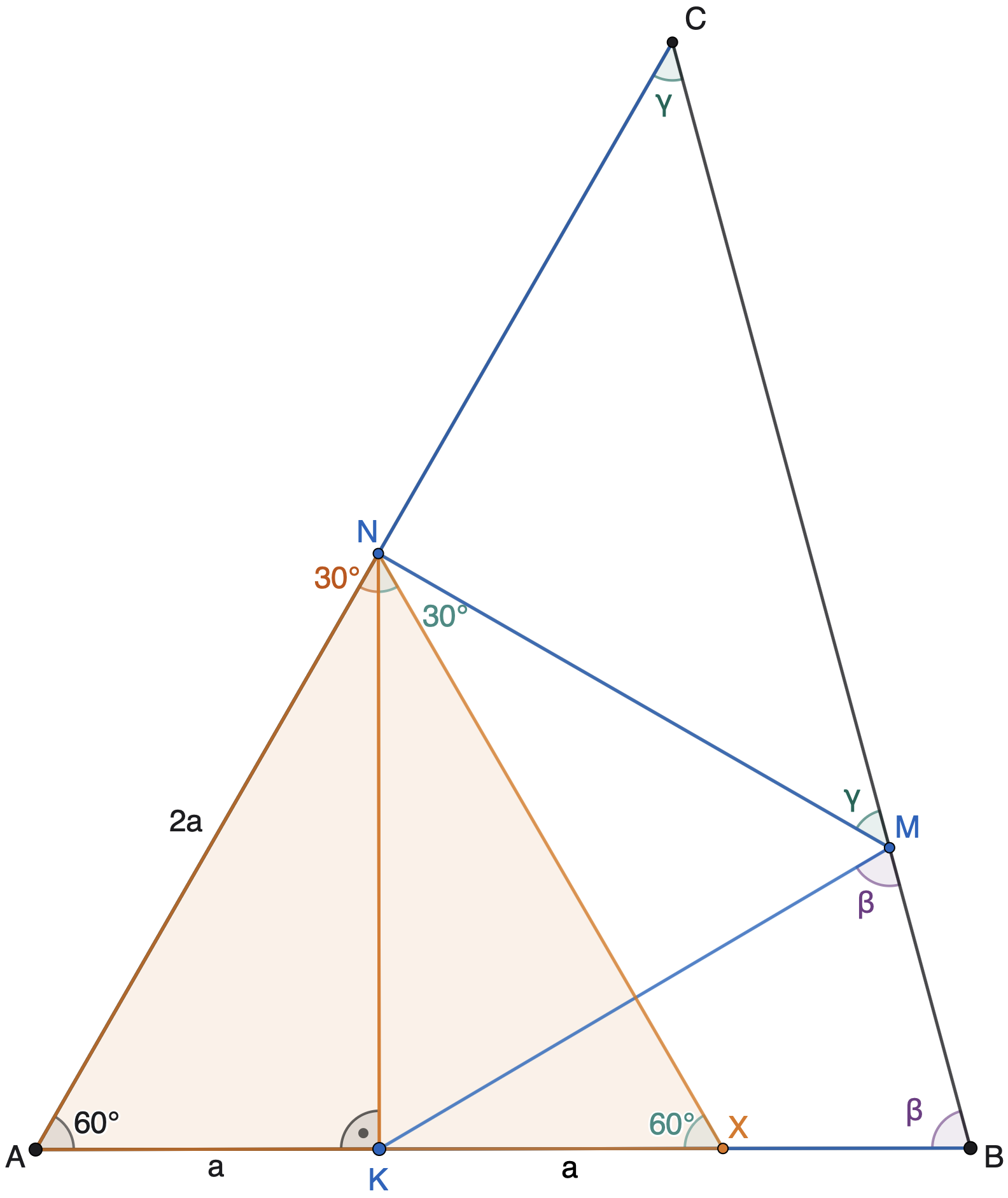
Trojuholník AXN je takto rovnoramenný, keďže \left| AX\right| = \left| AN\right|. Zo zadania však vieme, že \left|\angle BAC \right| = 60^\circ. Keď v rovnoramennom trojuholníku máme jeden uhol veľkosti 60^\circ, tak musia byť aj všetky ostatné uhly rovnakej veľkosti 60^\circ, a teda je tento trojuholník rovnostranný. Tým pádom je úsečka KN výška trojuholníku AXN na stranu AX, a teda \left|\angle AKN \right| = 90^\circ. Keďže v rovnostrannom trojuholníku každá výška delí uhol pri jej vrchole na polovicu, tak vieme, že \left|\angle ANK \right| = 30^\circ.

Teraz si poďme trochu zauhliť. Vieme už, že trojuholníky KBM a NMC sú rovnoramenné a platí, že súčet uhlov v trojholníku je 180^\circ, a teda vieme dopočítať uhly \left|\angle BKM \right| = 180^\circ - 2\beta a \left|\angle MNC \right| = 180^\circ - 2\gamma.

Všimnime si, že \left|\angle BKM \right| + \left|\angle NKM \right| + \left|\angle AKN \right| = 180^\circ, a teda keď už poznáme veľkosti uhlov \angle BKM a \angle AKN, vedeli by sme dopočítať uhol \angle NKM. Tak poďme na to! Vieme, že \left| \angle BKM \right| = 180^\circ - 2\beta a \left|\angle AKN \right| = 90^\circ, tak to môžeme dosadiť do rovnice a upravovať:

∣∠BKM∣+∣∠NKM∣+∣∠AKN∣=180^\circ

180 ^∘ −2β+∣∠NKM∣+90 ^∘ =180 ^∘

∣∠NKM∣=2β−90^\circ

Podobne si môžeme všimnúť, že ∣∠MNC∣+∣∠KNM∣+∣∠ANK∣=180^\circ, a teda vieme dopočítať uhol \angle KNM. Vieme, že \left| \angle MNC \right| = 180^\circ - 2\gamma a tiež \left| \angle ANK \right| = 30^\circ. Tak si to dosaďme do rovnice:

∣∠MNC∣+∣∠KNM∣+∣∠ANK∣=180^∘

180 ^∘ −2γ+∣∠KNM∣+30 ^∘ =180 ^∘

∣∠KNM∣+=2γ−30 ^∘

Oba tieto uhly čo sme si teraz vyjadrili sa nachádzjú v trojuholníku KMN, takže by sme sa naň mohli pozrieť trochu bližšie.

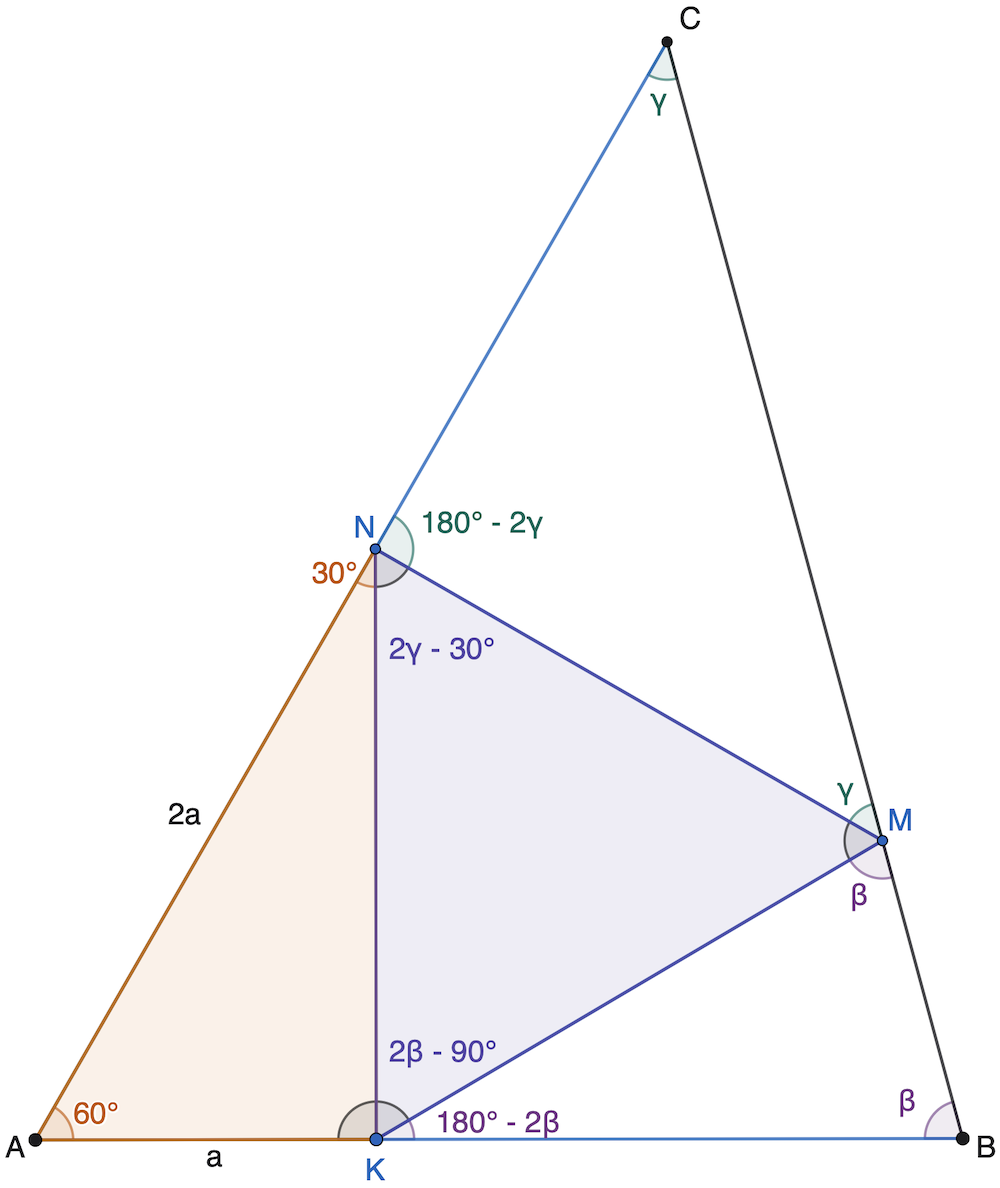
Zo zadania už vieme, že \left|KM \right| = \left| MN \right|. To znamená, že trojuholník KMN je rovnoramenný s základňou KN. Velkosti uhlov pri nej sa teda musia rovnať. Takže \left| \angle NKM \right| =\left| \angle KNM \right|. My sme však teraz vypočítali, že \left| \angle NKM \right| = 2β−90^∘ a \left| \angle KNM \right| = 2γ−30 ^∘. Teda dostávame rovnicu:

2β−90^∘=2γ−30 ^∘

Čo si vieme upraviť:

2β=2γ+60^∘β=γ+30^∘

Teraz sa vráťme späť k trojuholníku ABC. Všetky uhly v ňom majú dávať dokopy 180^\circ, teda:

60^\circ + \beta + \gamma = 180^\circ

My však vieme, že β=γ+30^\circ, čo vieme dosadiť do tejto rovnice:

60^\circ + \gamma + 30^\circ + \gamma = 180^\circ

2\gamma = 90^\circ

\gamma = 45^\circ

Takže sme zistili \left| \angle ACB \right| = 45^\circ. Teraz iba dopočítame:\left| \angle ABC \right| = 180^\circ - 60^\circ - 45^\circ = 75^\circ

Odpoveď: Veľkosť uhlu \angle ABC je 75^\circ a veľkosť uhlu \angle ACB je 45^\circ

Ako prvé si potrebujeme zadanie prepísať do nejakej rovnice, s ktorou budeme môcť pracovať - upravovať ju. Ak umiestnime znamienko krát medzi stovky a desiatky čísla, dostaneme súčin, označme si ho A\times B. Naše pôvodné číslo teda vyzerá ako \overline{aaabb} (kde ľubovoľný počet a-čok reprezentuje cifry čísla A, a \overline{bb} reprezentuje cifry čísla b), alebo inak povedané n=100\times A+B (\overline{aaa00}+\overline{bb}). Potom teda zadanie hovorí, že:

A\times B=\frac{100A+B}2

Z tejto rovnice si skúsime vyjadriť B úpravami:

2AB=100A+B

2AB-B=100A

B(2A-1)=100A

B=\frac{100A}{2A-1}

Vieme, že A aj B sú celé čísla. Neostáva teda príliš veľa možností, ako rovnicu vyriešiť. 2A-1 musí byť deliteľom 100A. Zároveň vieme, že 2A-1 je nesúdeliteľné s A, pretože všetky delitele A sú aj deliteľmi 2A, a číslo o 1 menšie isto deliť nebudú (okrem triviálneho deliteľa - jednotky). Takže 2A-1 musí byť deliteľom čisto 100-ky. Zároveň vieme že je to nepárne číslo, a nepárne delitele čísla 100=5\times 5\times 2\times 2 sú iba mocniny 5: 1, 5 a 25.

Z každého dostaneme konkrétnu hodnotu A (pripočítame 1 a vydelíme dvomi): 1, 3 a 13, a to už je dostatočne málo riešení na to, aby sme ich mohli len vyskúšať. Vieme, že žiadne iné riešenia nemôžu byť, pretože potom v akomkoľvek inom prípade by B nevychádzalo celé číslo.

Ak A=1:

B=\frac{100}1=100

To je viac ako 99, čo je najväčšie možné B, keďže je tvorené dvomi ciframi

Ak A=3:

B=\frac{100\times 3}{5}=60

n=360

vložíme krát:

3 \times 60=180=\frac{360}2

sedí, máme prvú odpoveď 360

Ak A=13:

B=\frac{100\times 13}{25}=52

n=1352

vložíme krát:

13\times 52=676=\frac{1352}2

sedí, druhá odpoveď je 1352

Odpoveď: 360; 1352

Pozrime sa na rozdiel hodnôt s(p\cdot q+800) a s(p\cdot q+799)

Ak posledná cifra p \cdot q nie je 0, rozdiel hodnôt bude 1, lebo p\cdot q+800 a p\cdot q+799 sa budú odlišovať iba na mieste jednotiek. 

Ak je posledná cifra p\cdot q  nula, aj posledná cifra p⋅q+800  bude 0. Ak od tohto čísla odčítame 1 aby sme dostali p\cdot q + 799, budeme musieť prechádzať cez desiatku, a teda rozdiel nebude 1.

Nech

  s(p\cdot q+800)- s(p\cdot q+799)=1

Pôvodná rovnica sa nám teda upraví na 1+s(p)\cdot s(q+1)=s(2p), pričom s(2p) bude najviac 2\cdot s(p), a to vtedy, keď neprechádzame cez desiatku. 

Rovnicu si teda vieme upraviť na

s(p)\cdot s(q+1)+1<=2\cdot s(p)

Z toho vidíme, že s(q+1) je najviac 1. Na to ale q musí byť buď 0 alebo mať iba cifry 9 (napríklad 9999). Pri oboch týchto možnostiach však q nie je prvočíslo (číslo zo samých 9 má ciferný súčet deliteľný 9, teda je deliteľné 3aj 9), a preto táto možnosť nefunguje.

Pozrime sa teraz na druhú možnosť, kedy posledná cifra p\cdot q je 0. p\cdot q potom musí byť deliteľné 10, a keďže p aj q sú prvočísla, jediná možnosť je, že jedno z nich je 2 a druhé 5, lebo 10=5\cdot 2.

Ak p=5, q=2:

 s(2\cdot 5+800)+s(5)\cdot s(2+1)=s(2\cdot 5+799)+s(2\cdot 5)

s(810)+s(5)\cdot s(3)=s(809)+s(10)

9+15=17+1

24\neq18

Táto možnosť teda nefunguje.

Ak p=2,q=5:

s(2\cdot5+800)+s(2)\cdot s(5+1)=s(2\cdot 5+799)+s(2\cdot2)

s(810)+s(2)\cdot s(6)=s(809)+s(4)

9+12=17+4

21=21

Jediné riešenie je teda p=2, q=5

Rozdelíme si úlohu na dva prípady podľa toho, či je N párne. Ak je totiž N nepárne, výhru si vie Lukáš zaručiť jednoducho:

Lukáš bude začínajúci hráč a pridá jednu kostičku. Tým bude na kôpke nepárny počet kostičiek. Či už pútnik pridá jednu kostičku alebo vynásobí počet kostičiek dvomi, po jeho ťahu bude na kôpke párny počet kostičiek. To platí pre akýkoľvek nepárny počet kostičiek na kôpke. Potom Lukáš zase pridá 1 kostičku, čím vytvorí nepárne číslo. Takto sa budú striedať, až kým Lukáš nepoloží N-tú kostičku. Položí ju on, lebo pútnik nemá ako zabrániť tomu, aby po Lukášovom ťahu bol na kôpke nepárny počet, lebo vždy dostane nepárny počet z neho musí urobiť párny.

Ak je N párne, už nevidíme takú priamočiaru stratégiu, preto sa budeme musieť na hru pozrieť viac systematicky. Budeme sa pozerať na to, ktoré pozície sú vyhrávajúce a ktoré prehrávajúce (pozíciou sa myslí stav hry, teda to, aký počet kostičiek je na kôpke, keď ideme urobiť ťah).

Prvá prehrávajúca pozícia je, keď je na kôpke N kostičiek. Vtedy už nemôžeme urobiť ťah. Pozícia s N-1 kostičkami je zase vyhrávajúca, lebo vieme súpera dostať do prehrávajúcej tým, že pridáme 1 kostičku. Podobne aj pozícia s \frac{N}2 kostičkami, lebo vieme zdvojnásobiť počet kostičiek a súper opäť prehráva. Všeobecne platí, že ak sa vieme z pozície dostať ťahom na prehrávajúcu, je vyhrávajúca. Ak však nevieme súpera dostať do situácie kedy zaručene prehrá, teda sa vieme dostať iba na vyhrávajúce, tak je prehrávajúca. 

Takúto úvahu má zmysel robiť, pretože hra je "priamočiara" - nemôžeme sa vrátiť späť do nejakej minulej pozície. Preto sa dá určiť, či je každá pozícia vyhrávajúca alebo nie tým, že pôjdeme od konca. Ak poznáme stav všetkých pozícií, na ktoré sa vieme dostať, použijeme na určenie vyššie opísané pravidlo.

Pre počty medzi \frac{N}2 a N vieme tiež jasne určiť, či hráč na ťahu vyhrá, teda či sú vyhrávajúce alebo prehrávajúce. Hráči totiž už nemôžu násobiť dvomi, musia iba pridávať 1 kostičku. Hráč, ktorý je v pozícii s hocijakým párnym počtom kostičiek väčším ako \frac{N}2 sa už nevie dostať do pozície s nepárnym počtom kostičiek, pretože pridaním 1 kostičky vytvorí nepárne číslo a jeho súper potom zasa párne. Teda to bude práve jeho súper, ktorý na konci dosiahne N. Všetky párne pozície väčšie ako \frac{N}2 sú teda prehrávajúce (a všetky nepárne vyhrávajúce).

Ale čo ak na ťahu máme menej kostičiek? Kedy vieme dostať súpera do prehrávajúcej pozície? Vieme už, že všetky párne pozície väčšie ako \frac{N}2 sú prehrávajúce. Takže ak dostaneme hocijaké číslo väčšie ako \frac{N}4, ale nanajvýš \frac{N}2, môžeme ho zdvojnásobiť. Tým vytvoríme súperovi jednu z prehrávajúcich pozícií a on nakoniec prehrá.

Máme teda "vyhrávajúce pásmo" ktoré obsahuje všetky pozície nad \frac{N}4 do \frac{N}2. Toto pásmo je zaujímavé tým, že sa nedá preskočiť - vždy aspoň jeden hráč musí vytvoriť takúto pozíciu. Aj keby na ťahu mal najväčšie menšie číslo a zdvojnásobil by ho, nad toto pásmo sa nedostane. Hráč ktorý toto urobí zároveň aj prehrá, lebo dostane súpera do vyhrávajúcej pozície. Tým že hráči nesmú presiahnuť \frac{N}4, môžeme si povedať, že pôvodná hra s N je ekvivalentná tomu, akoby hráči hrali iba s maximom M=\lfloor \frac{N}4 \rfloor (zápis znamená zaokrúhlenie nadol, číslo \frac{N}4 nemusí existovať, ale hľadáme najväčšie, ktoré nie je väčšie). Nemajú síce zakázané robiť ťahy ktoré toto číslo presiahnu, ale zaručia si tým prehru.

Ak je M nepárne, Lukáš dokáže vyhrať stratégiou, ktorá je opísaná v prvej časti riešenia. Ak je číslo párne, musíme zopakovať úvahu o stratégii pre párne N. Zistíme teda, že pozícia \lfloor \frac{M}4 \rfloor je prehrávajúca a pozrieme sa, ako na ňu vie Lukáš dostať pútnika. Teda v prípade potreby zase úvahu opakujeme.

Ak v tomto procese narazíme na nepárne číslo, môžeme poradiť Lukášovi, že má začínať, aby naň vedel dostať súpera neustálym pričítavaním 1. Po dosiahnutí tohto nepárneho čísla (alebo keď ho pútnik presiahne) už pokračuje tak, aby vždy išiel na prehrávajúce pozície tak, ako sme ich opísali. 

Môže sa ale stať, že budú všetky čísla párne? Pri operácii delenia kladného čísla 4 a prípadnom zaokrúhlení sa číslo vždy musí zmenšiť, a teda jediná možnosť, ako by sme mohli mať samé párne čísla je, že sa eventuálne dostaneme na 0. To nám hovorí, že byť na ťahu s 0 kostičkami na kôpke je prehrávajúce, a teda Lukáš by nemal začínať.

Odpoveď: Lukáš by mal začínať, ak je N nepárne alebo ak sa opakovaným delením N štyrmi a zaokrúhľovaním nadol dostaneme na nepárne číslo. Lukáš vie na dané nepárne číslo súpera dostať tak, že vždy bude iba pridávať 1 kostičku. Potom zdvojnásobuje iba vtedy, ak jeho súper v predošlom ťahu práve presiahol jedno z čísel ktoré opakovaným delením vzniklo.

Označíme si A_B, A_C, B', C' postupne A preklopené cez CI, A preklopené cez BI, B preklopené cez CI a C preklopené cez BI. Potom priamka AB preklopená cez CI je priamka A_BB'. Podobne priamka AC preklopená cez BI je priamka A_CC'. Teda bod X je priesečník priamok A_BB' a A_CC'. Nakoniec si označme E = BI \cap AC a F = CI \cap AB.

Bod A_B leží na priamke BC, keďže |\sphericalangle A_BCI| = |\sphericalangle ACI| = |\sphericalangle ICB|, kde prvú rovnosť máme z definície bodu A_B a druhú rovnosť máme z toho že I je stred kružnice vpísanej ABC, teda CI je os uhla \sphericalangle BCA. Rovnakým argumentom môžeme dostať, že A_C leží na priamke BC, C'B' leží na priamke AC a C' leží na priamke AB.

Keďže A_B je A preklopené cez CI a keďže F \in CI, tak |\sphericalangle A_BFC| = |\sphericalangle CFA|. Ďalej už vieme, že |\sphericalangle A_BCF| = |\sphericalangle FCA| a taktiež |CF| = |CF|. To znamená, že trojuholníky A_BCF a ACF sú zhodné. Z toho dostávame, že |\sphericalangle BAC| = |\sphericalangle CA_BB'|. Analogicky vieme dostať, že trojuholiky ABE a A_CBE sú zhodné, teda |\sphericalangle BAC| = |\sphericalangle EA_CC|. Spojením rovností dostávame, že |\sphericalangle EA_CC| = |\sphericalangle CA_BB'|, teda trojuholník A_BA_CX je rovnoramenný so základňou A_BA_C.

Nech \omega je kružnica vpísaná trojuholníku ABC. Preklopenie \omega cez priamku BI je zase \omega, keďže BI prechádza jej stredom I. To znamená, že keď AC sa dotýkalo \omega, tak potom aj preklopenie AC, priamka A_CC', sa dotýka \omega. Analogicky sa A_BB' dotýka \omega. Keďže sa však aj BC dotýka \omega, tak sme dostali, že \omega je kružnica vpísaná trojuholníku A_BA_CX. To však ale znamená, že XI  je os uhlu \sphericalangle A_BXA_C. Avšak keďže A_BA_CX je rovnoramenný, tak os uhlu a výška oproti základni splývajú, teda XI je tiež výška v trojuholníku A_BA_CX, teda XI \perp BC.