Vzorové riešenia 2. kola

V zadaní nám bolo naraz daných pomerne veľa informácii. Dôležité je si v nich spraviť poriadok.
To, čo zistíme si budeme prehľadne spisovať napríklad do takejto tabuľky:

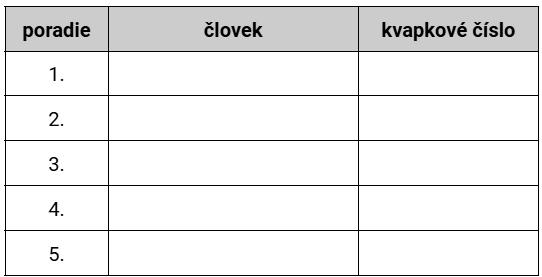
Začneme treťou podmienkou (Prvá prišla Zuzka Š. alebo Kai.). Na prvom mieste máme teda dve možnosti, Zuzka Š. a Kai. V tabuľke v tomto prípade použijeme slovíčko “alebo”.

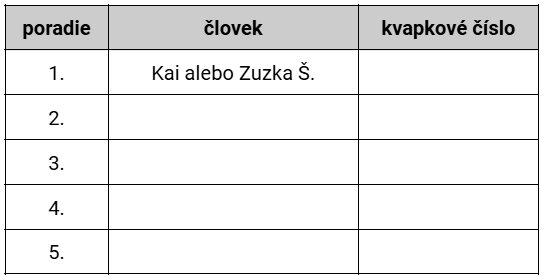
Pokračovať budeme štvrtou podmienkou (Súčin kvapkových čísel tretieho a štvrtého človeka je 56​.). Vieme, že 7\cdot8=56​. 7 je prvočíslo a 8=2\cdot2\cdot2​, ale my 2​ medzi kvapkovými číslami nemáme. To znamená, že na tretej a štvrtej pozícii musia byť práve čísla 7​ a 8​. Keďže máme opäť viac možností, použijeme “alebo” a jednotlivé možnosti si vyfarbíme.
Ak na treťom mieste bude 7​, na štvrtom bude automaticky 8​ (modrá možnosť). Ak bude na treťom 8​, na štvrtom musí byť 7​ (červená možnosť).
Tabuľka teda vyzerá takto:

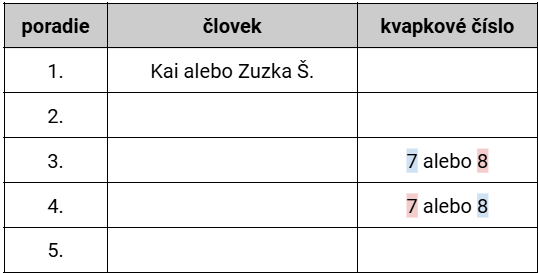
Poďme sa teraz pozrieť na prvú podmienku (Súčet kvapkových čísel ľudí, ktorí prišli skôr ako Sebik, je menej ako 7​.). Pred Sebikom, teda nemôže byť vedúci, ktoré má kvapkové číslo 7​ alebo 8​. To znamená, že Sebik musí byť aspoň tretí (aby mohli byť vedúci s týmito číslami za ním). Ak by pred ním bol vedúci s kvapkovým číslom 6​, nemohol by byť pred Sebikom nikto iný, iba tento vedúci (zelená možnosť). Ešte vedia byť pred Sebikom vedúci s kvapkovým číslom 3​, buď jeden (žltá možnosť), alebo dvaja (fialová možnosť), stále bude podmienka splnená. Zapíšeme si to, pričom rôzne scenáre opäť farebne odlíšime, ako uvádzame v zátvorkách:

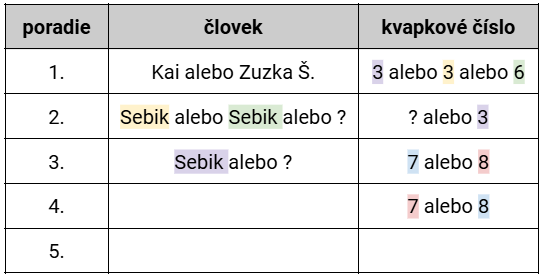
Teraz sa pozrieme na piatu podmienku (Prutky ako jediný prišiel medzi Zuzkou Š. a Majkom.). Ak by bola Zuzka Š. prvá, potom by druhý musel byť Prutky a tretí Majko. Takže Sebikovi by nezostalo miesto. To znamená, že prvý bude Kai:

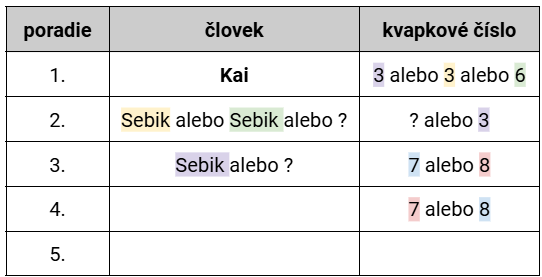
Vieme, že Zuzka Š., Prutky a Majko prišli tesne za sebou v nejakom poradí. Ak by Sebik bol tretí, nemáme tri neobsadené po sebe idúce miesta. Sebik teda bude druhý a títo traja budú na treťom, štvrtom a piatom mieste. Prutky bude uprostred (je medzi Majkom a Zuzkou Š.), čiže na štvrtom mieste. Pre Zuzku Š. a Majka máme dve alternatívy (oranžovú a fialovú).

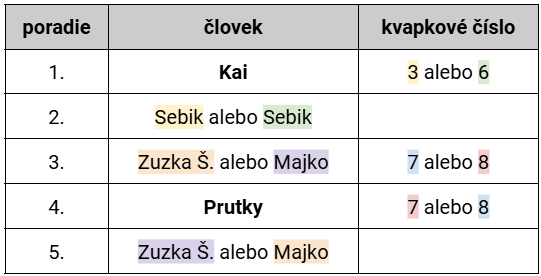
Zostala druhá podmienka (Majko, Sebik a Prutky majú nepárny súčin kvapkových čísel.). Hovorí sa tam o nepárnom súčine kvapkových čísel. Ako taký súčin docieliť? Tu si treba uvedomiť, že nepárny súčin nesmie obsahovať ani jedno párne číslo. To znamená, že Majko, Sebik a Prutky musia mať len nepárne kvapkové čísla. Keďže takéto čísla sú práve tri, vieme, že Majko, Sebik a Prutky budú mať v nejakom (zatiaľ neznámom) poradí kvapkové čísla 3​, 3​, a 7​. Zuzke Š. a Kaiovi teda zostanú čísla 6​ a 8​.
Ak sa pozrieme do tabuľky, pri Prutkym máme na výber buď 7​ alebo 8​. Dáme mu teda číslo 7​. To znamená, že pre Majka a Sebika zostali čísla 3​. Zároveň to znamená, že vedúci na treťom mieste má číslo 8​. Bude to teda Zuzka Š., keďže Majko má mať 3​.
Pri Kaiovi máme na výber 3​ alebo 6​, dostane teda 6 (čo je číslo, ktoré aj zostalo, takže všetko vychádza).

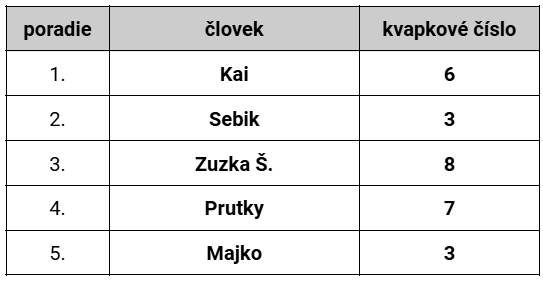
Možno ste si pri čítaní vzorového riešenia kládli jednu z týchto otázok:

• Prečo sme tie podmienky rozoberali práve v tomto poradí?
• Odkiaľ som mal/-a vedieť, že si potrebujem spraviť práve takúto tabuľku? Prečo sme priraďovali mená a kvapkové čísla k poradiu? Nemohli sme poradie a kvapkové čísla priraďovať k menám? Alebo poradie a mená priraďovať ku kvapkovým číslam?

Nuž, ani na poradí, ani na tabuľke nezáleží. Riešenie vyjde vždy rovnaké. Môžete si skúsiť sami ako cvičenie rozobrať podmienky v inom poradí a s inými tabuľkami a overiť si to 🙂.
My sme vo vzorovom riešení zvolili túto tabuľku a takéto poradie, keďže nám to prišlo najjednoduchšie na pochopenie.

Zadanie nám o tabuľke ponúka veľa informácii. Aby sme zistili, aké čísla vedia byť v tabuľke, treba týmito informáciami nejako štrukturovane postupne prechádzať a skúsiť z nich vyťažiť čo najviac.

Prvým takým zaujímavým pozorovaním je, že horný riadok má dve čísla. Súčet najväčších dvoch cifier bude teda 13 a súčet najmenších dvoch bude 5. Keďže máme v riadku ale len tri cifry, znamená to, že jedna z nich (tá stredne veľká) bude v oboch týchto súčtoch.

To isté platí aj pre pravý stĺpec, keďže tam máme hore 11 a dole 9.

Ďalej sa v zadaní spomína, že tabuľku vypĺňame ciframi od 1 do 9 a každú použijeme práve raz. To znamená, že najväčší možný súčet vie vzniknúť súčtom dvoch najväčších cifier 9 + 8 = 17. Čo si môžeme všimnúť je číslo 16 pre prostredný stĺpec. Je len o 1 menšie od 17, takže možnosti ako dostať 16 sú 8 + 8 = 16 (to sme akoby znížili o 1 cifru 9 v súčte 9 + 8 = 17) a 9 + 7 = 16 (to sme akoby znížili o 1 cifru 8 v súčte 9 + 8 = 17). Keďže sú ale cifry v tabuľke rôzne, určite sa využije druhá možnosť. Takže v prostrednom stĺpci budú cifry 9 a 7. Zatiaľ ale ešte nevieme, kde presne môžu byť.

Teraz sa pozrime na napríklad na 13 v hornom riadku. Súčet 13 vieme získať ako 9 + 4, 8 + 5 alebo 7 + 6. Všimnime si ale, že v rovnakom riadku je aj 5, ktorú vieme získať len ako 1 + 4 alebo 2 + 3.

My už ale vieme, že jedno číslo musia mať tieto súčty spoločné. Teda pre 13 nám zostáva len možnosť 9 + 4 a pre 5 nám zostáva možnosť 1 + 4, keďže toto je jediná dvojica súčtov, ktorá má spoločné jedno číslo, konkrétne 4. V hornom riadku musia byť čísla 1, 4, 9.

My sme ale už prišli na to, že 9 potrebujeme aj v prostrednom stĺpci. To znamená, že vieme jej finálnu polohu.

Pozrime sa teraz späť na prostredný stĺpec. Vieme, že v ňom musí byť 7 a máme už 9 v hornom políčku, teda 7 môže byť buď v strede alebo dole. V prostrednom riadku máme zadaný súčet 14. Ak by v tomto riadku bola 7, tak nemôže byť súčasťou súčtu 14, lebo druhé číslo tohto súčtu by tiež muselo byť 7, aby platilo 7 + 7 = 14, a potom by sa nám cifry opakovali.

To by ale znamenalo, že zvyšné 2 cifry sú buď obe menšie, alebo obe väčšie a dávajú súčet 14. Ak sú ale obe väčšie (menšie) ako 7, tak aj ich súčet bude väčší (menši) ako 2 \cdot 7 = 14. Teda ak chceme splniť súčet 14, tak 7 nemôže byť v strede a bude v spodnom políčku.

Teraz sa pozrime na pravý stĺpec. V tomto stĺpci máme zadané dva súčty (11​ a 9​) a už vieme, že v hornom políčku musí byť buď 1 alebo 4. Poďme zistiť, ktorá z týchto dvoch cifier tam môže byť.

Súčet dvoch najmenších cifier v tomto stĺpci je 9. Ak by 1 bola jednou z nich, tá druhá by musela byť 8. Lenže aby sme mali splnený aj súčet 11, posledná cifra v tomto stĺpci by musela byť 3. Potom by ale súčet dvoch najmenších cifier nebol 1 + 8 = 9, ale 1 + 3 = 4. Z toho teda vyplýva, že 1 v hornom políčku byť nemôže. To znamená, že 4 bude vpravo hore a 1 vľavo hore.

Teraz sa pozrime na pravý a ľavý stĺpec. V každom sú ešte dve prázdne políčka, ktorých súčet má byť 11. (Cifry 1 a 4, ktoré tam už sú, na tento súčet nevieme využiť, keďže k 1 by sme potrebovali 10, čo nie je cifra a k 4 by sme potrebovali 7, ktorú sme už použili). Súčet 11 vieme získať ako 9 + 2, 8 + 3, 7 + 4 a 6 + 5. Cifry 9 a 7 sme už ale použili v prostrednom stĺpci, takže zostávajú možnosti 8 + 3 a 6 + 5.

Ak by v pravom stĺpci boli čísla 3, 4 a 8, tak súčet najväčších 2 cifier je 4+8=12 a najmenších dvoch 3+4=7. Teda táto možnosť nesedí. Ale ak by tam boli čísla 4, 5 a 6 tak súčet najmenších dvoch je 4+5=9 a najväčších dvoch je 5+6=11.

Teda v pravom stĺpci sú čísla 4, 5, 6 a v ľavom 1, 3, 8.

Zostávajúce číslo 2 bude v prostrednom stĺpci.

Teraz sa nám už stačí pozrieť na prostredný riadok. Tam je číslo 14, ktoré vieme dostať ako 9+5, 8+6 alebo 7+7. Keďže cifru 9 sme už použili v hornom riadku a pri súčte 7+7 sa cifry opakujú, v prostrednom riadku budú cifry 8 a 6.

Tabuľka je týmto kompletne vyplnená:

Skúsme si najprv spočítať, koľko má takáto mriežka hrán. V každom riadku a stĺpci máme po 5​ hrán a riadkov aj stĺpcov tam je 6. Dokopy je to teda 6\cdot2\cdot5=60​. Máme 6​ hadov dĺžky 10​, teda 60​ kusov hada. Počty teda sedia, z tohto pohľadu by pokrytie všetkých hrán mohlo byť možné.

Ak sa však pokúsime kobry rozmiestňovať, nepodarí sa nám zadanie splniť. Možno si aj všimneme, že niektoré hrany sa nám pokrývajú nejako ťažšie (tie pri krajoch) a možno to súvisí aj s mrežovými bodmi (vrcholmi). Práve na tie sa skúsime zamerať.

Všimnime si, že keď cez vrchol mriežky prechádza had, musí vojsť cez jednu hranu a vyjsť cez druhú. Pri svojom prechode teda zaberie dve hrany. Bežným vrcholom, z ktorého vychádzajú 4 hrany teda prejdú dva hady. Na okraji mriežky ale máme vrcholy, z ktorých vychádzajú tri hrany. V týchto vrcholoch musí nejaký had začínať alebo končiť. Prechádzajúci had totiž zaberie dve z troch hrán, poslednú vyplní had už len tak, že príde a nemá kam ďalej ísť, alebo tam naopak začne.  

Vrcholy, z ktorých vychádzajú tri hrany, sú na každej strane mriežky štyri, takže dokopy máme 4\cdot4=16​ takýchto vrcholov. V každom z nich musí začínať alebo končiť had, inak nejaká hrana pri ňom isto ostane nezaplnená. K dispozícii máme šesť hadov a každý má dva konce, teda 12​ koncov hada. Vidíme, že mriežka sa nedá vyplniť, lebo nemáme dosť koncov hada.

​Najprv si napíšme zadanie v tvare rovníc, nech kúsok lepšie vidíme, čo sa tam deje:

​A\cdot C=B+2

B \cdot D=A+1

Ešte predtým ako sa pozrieme na tento príklad, tak sa pozrime na podobný vírazne jednoduchší príklad a to:

​A\cdot C=B

B \cdot D=A

Uvedomme si, že C je aspoň 1, keďže všetko to sú prirodzené čísla, tak prvá rovnica nám dáva, že A\leq B. Podobne z druhej rovnice dostávame, že B \geq A, čo jednoducho vedie k tomu, že A=B a C=D=1.

S podobnou myšlienkou vieme pristúpiť k pôvodnej dvojici rovníc. Číslo C je aspoň 1, takže ak A\cdot C=B+2, tak A\leq B+2. Z druhej rovnice rovnako dostávame, že B\leq A+1. Keď odčítame 1, tak máme B-1\leq A. To si vieme napísať ako sériu nerovností:

​B-1\leq A \leq B+2​​

Máme teda 4 možnosti, pričom jednu možnosť A=B nám priamo zakazuje zadanie.

Ostávajú nám 3 možnosti, ktoré postupne preveríme:

1. A=B-1, respektíve B=A+1​

Dosaďme B=A+1, do prvej rovnice a dostávame:

​A\cdot C=A+3​
Prehoďme A na ľavú stranu a vyberme pred zátvorku:

​A\cdot C-A=3

A\cdot( C-1)=3​​

Vidíme, že súčin dvoch prirodzených čísel je 3, avšak nie je moc prirodzených čísel, ktoré majú súčin 3, konkrétne 3=3\cdot 1. Máme teraz 2 možnosti:

Buďto A=3 a C-1=1. V tom prípade si ľahko priamim dosadením do pôvodných rovníc dorátame, že C=2, B=4 a D=1, alebo A=1​ a C-1=3. V tom prípade dostávame, že C=4, B=2 a D=2.

2. A=B+1​, respektíve B=A-1

Dosaďme B=A-1, do prvej rovnice a dostávame:

​A\cdot C=A+1​
Podobne ako v minulom prípade, jednoducho upravíme do tvaru :

A\cdot( C-1)=1

Aby súčin 2 prirodzených čísel bol 1, tak obe čísla potrebujú byť 1. Čím dostávame:

A=1 a C-1=1. Avšak ak A=1, tak B=A-1=1-1=0, čo však nie je prirodzené číslo a tento prípad nevedie k žiadnemu riešeniu.

3. Posledné čo nám ostáva je poriešiť prípad A=B+2. Všimnime si však, že keď tento víraz dosadíme do druhej rovnice, tak dostaneme:

​B\cdot D=B+3, ide o rovnakú rovnosť ako v prvom prípade. Takže úplne rovnakým postupom dostávame:

Buďto B=3 a D-1=1. Potom D=2, A=5 a C=1, alebo B=1​ a D-1=3. Priame dosadenie vedie k výsledkom D=4, A=3 a C=1​.

Existuje veľa možností, ako mohli zápasy prebehnúť, a ako hráči mohli nazbierať svojich 8, 7​, 4​ a 4​ bodov. Skúsme sa preto najprv zamerať iba na to, koľko bodov dokopy hráči môžu a potrebujú získať.

Celkový počet bodov sa zisťuje jednoducho aj preto, že v každom zápase sa udelia presne 2​ body. V prípade výhry jedného hráča dostane on všetky 2​ a v prípade remízy dostanú obaja po jednom, v súčte znova 2​. Preto ak zistíme, koľko zápasov sa odohralo, budeme aj vedieť celkový počet získaných bodov.

Počet hráčov zatiaľ nepoznáme, označme si ho teda neznámou n. Vieme, že každý z n hráčov hral n-1 zápasov (nemôže hrať sám so sebou). Vynásobením n \cdot (n-1) však zarátame každý zápas z pohľadu oboch hráčov, preto ​pre n hráčov bude \cfrac {n(n−1)}{2} zápasov.

Teda udelených bodov celkovo bude \cfrac {n(n−1)}{2}\cdot2=n(n−1)​

Keď poznáme tento jednoduchý vzorec na výpočet získaných bodov, môžeme sa postupne pozrieť na prípady s konkrétnym počtom hráčov. Pôjdeme od najmenšieho postupne smerom nahor.

​4​ hráči, ktorí sú spomenutí v zadaní, sú minimálny počet. V takom prípade je ich celkový počet bodov 8+7+4+4=23. Podľa nášho vzorca ale získajú dokopy iba 4 \cdot 3= 12 a to nie je dosť, aby každý získal svoje body. Musí ich teda byť iný počet.

Pre 5 hráčov máme podľa vzorca 5 \cdot4=20 bodov, čo stále nie je dosť ani pre prvých štyroch hráčov, ktorí získali spolu 23 bodov (alebo by piaty musel získať záporný počet bodov, čo nemôže, lebo sa dajú získavať len nezáporné počty bodov).

Pre 6 hráčov zo vzorca vychádza, že budú mať polu 6 \cdot 5=30 bodov. To by mohlo fungovať, keďže prví štyria majú 23 bodov, a zvyšní dvaja teda musia mať spolu 30-23=7 bodov. Zároveň však vieme, že ani jeden z nich nemôže mať viac ako 4 body, lebo inak by predbehli 4.​ miesto. Nemôžu mať obaja ani menej ako 4 body, lebo by získali najviac 3+3=6 bodov. Teda jeden z nich musí mať 4 body, a potom druhý musí mať 7-4=3 body.

Teraz musíme ešte nájsť riešenie, lebo to nie nutne musí existovať. Zatiaľ sme iba ukázali, aké počty bodov dosiahnu, ak existuje riešenie pre 6​ hráčov (napríklad rozloženie 10,9,5,3,2,1 nevieme dosiahnuť napriek tomu, že má správny súčet). V tomto prípade sa nám ho podarí nájsť. V tabuľke je opísané tak, že každý hráč má riadok so svojimi bodmi v stĺpci hráča, s ktorým ich získal.

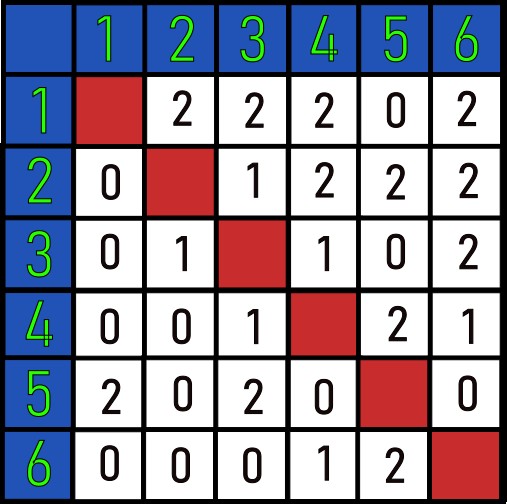
Tu však nekončíme, potrebujeme sa pozrieť, čo s možnosťami väčšími než 6​.

Pre 7 hráčov máme 6\cdot7=42​ bodov, a 3 ľudí s neznámym počtom bodov. Tí si musia rozdeliť zvyšných 42-23=19  bodov, ale každý z nich môže mať (ako sme už spomínali), len 4  body. Spolu môžu mať maximálne 3\cdot 4=12 bodov, teda to nebude vychádzať, bodov bude naopak príliš veľa.

Aj pri väčších počtoch sa nám stane, že bodov bude príliš veľa. Poďme to teda nejak dokázať, aby sme mali istotu. Pre každý o 1​ vyšší počet sa nám zväčší počet bodov, ktoré mohli získať o 4(pribudne nový hráč, ktorý môže mať maximálne 4​ bodoy). Počet bodov, ktoré si musia rozdeliť sa ale zväčší o 2\cdot n, kde n je počet hráčov bez neho (to preto, lebo on zahrá nové zápasy so všetkými hráčmi, ktoré by sa bez neho nehrali, a zápas udelí 2 body).

2n je však pre náš počet určite viac ako 4, lebo najnižšie n​ čo dosadzujeme je 7.

Teda sme dokázali, že už teraz privysoký počet bodov na rozdelenia sa vždy zvýši viac, ako sa zvýsi počet ktorí vedia získať. 

Jediný počet hráčov, pre ktorý existuje riešenie je 6, a jediná možnosť na rozdelenie bodov zvyšným hráčom je 4 a 3.​

Na začiatok sa zamyslime nad tým, či vieme nejako donútiť súpera, aby prehral. Každé kladné celé číslo k je deliteľné číslom 1 a číslom k.Ak sú tieto dve čísla rôzne (k \neq 1), tak máme vždy aspoň dve možnosti, ako spraviť náš ťah. Číslo k môže mať aj ďalších deliteľov, no tie nás zatiaľ nezaujímajú. Aby súper prehral, potrebujeme, aby odčítal k. Nemôžeme sa však spoliehať na to, že to spraví len tak sám od seba. Ak bude mať na výber, tak odčíta iné číslo, takže jediný spôsob, ako zaručiť súperovu porážku, je dostať pred neho číslo 1.

Číslo 1 je takzvaná prehrávajúca pozícia, teda hráč z nej nevie vyhrať bez chyby súpera. Naopak, číslo 2 je vyhrávajúca pozícia, lebo odčítaním 2-1 = 1 dostaneme súpera do prehrávajúcej pozície, čím si zaistíme víťazstvo (ak nespravíme chybu). To, ktorý hráč má víťaznú stratégiu pre dané n, záleží od toho, či je n vyhrávajúca alebo prehrávajúca pozícia. V prvom prípade vie začínajúci hráč zariadiť svoje víťazstvo, v opačnom prípade to dokáže druhý hráč.

Teraz by sme sa vedeli pozrieť zaradom na čísla 3, 4, 5, \ldots a zisťovať, či z nich vieme dostať súpera do prehrávajúcej pozície. Ak áno, dané číslo zodpovedá vyhrávajúcej pozícii, ak nie, tak je to pozícia prehrávajúca. Napríklad z čísla 3 vieme buď odčítaním 1 dostať súpera do vyhrávajúcej pozície (2) alebo rovno prehrať odčítaním čísla 3. Takže 3 je prehrávajúca pozícia.

Tento postup nám síce čo-to naznačí pre menšie čísla, no my skrátka nevieme vyskúšať všetky prirodzené čísla. Musíme prísť teda s nejakými všeobecnými pozorovaniami.

Napríklad na začiatku sme si všimli, že v každom ťahu vieme odčítať číslo 1. Ak teda máme prehrávajúcu pozíciu pre nejaké n, tak z čísla n+1 vieme odčítaním 1 dostať súpera do prehrávajúcej pozície.Napríklad n=3 je prehrávajúca pozícia, takže ak sa dostaneme do situácie, že je pred nami číslo 4, tak vieme zabezpečiť, aby súper získal 4 - 1 = 3, čím ho vieme donútiť prehrať. Avšak dokázať, že niečo je prehrávajúca stratégia je ťažšie. Na to musia všetky delitele čísla n viesť do vyhrávajúcej pozície, inak si súper môže vybrať takú cestu, ktorou sa prehre vyhne.

Skúsme sa teda zamyslieť nad tým, ktoré čísla by mohli byť ktoré. Zatiaľ vieme, že 1 a 3 sú prehrávajúca pozície, kým 2 a 4 sú vyhrávajúce.Z toho sa dá odvodiť viacero záverov, no ľahko si vieme vyskúšať ďalšie čísla. To by nás malo presvedčiť, že párne čísla budú vyhrávajúce a nepárne prehrávajúce. Otázkou ostáva, prečo?

Je jasné, že z párneho čísla vieme spraviť nepárne tým, že odčítame číslo 1.Aké máme možnosti pri nepárnom čísle? Keďže nepárne číslo nie je deliteľné 2, tak nie je deliteľné ani násobkami 2. Všetky jeho delitele sú teda nepárne. A keďže odčítaním nepárneho čísla od nepárneho dostaneme párne číslo, tak je jasné, že ľubovoľný ťah ponúkne súperovi párne číslo. Súper odčíta 1 a opäť budeme v rovnakej situácii s nepárnym číslom.

To znamená, že hráč s párnym číslom vie zabezpečiť, aby pred jeho nasledujúcim ťahom opäť dostal párne číslo (alebo to súper "vzdá" a rovno skočí na 0). Postupne budú čísla menšie a menšie, až hráč dostane číslo 2, o ktorom už vieme, že je víťazná pozícia.

Odpoveď: Ak je n párne, tak vyhrá začínajúci hráč. Ak je n nepárne, tak vyhrá druhý hráč.

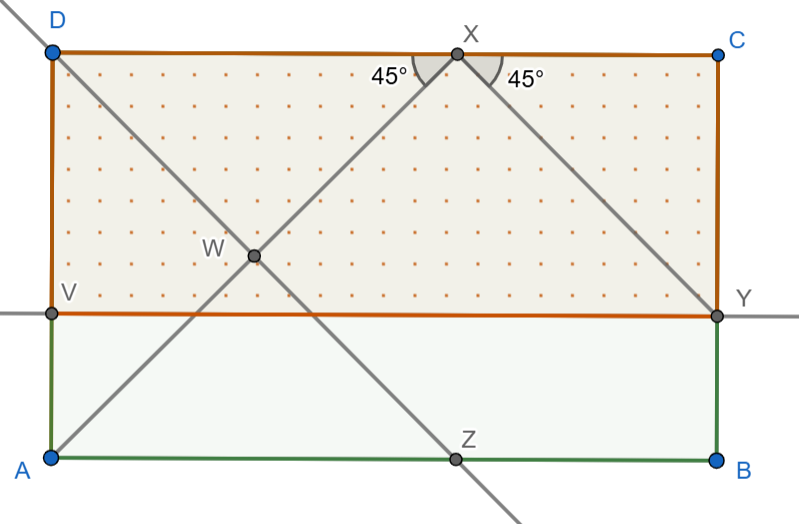
Vieme, že ABCD​ je obdĺžnik a teda všetky uhly má pravé. Týmito pravými uhlami sú aj ∡BCD​ a ∡CDA. To sú zároveň aj uhly trojuholníkov ΔYCX​ a ΔADX​, ktoré sú teda pravouhlé. Zo zadania poznáme ešte jeden ich uhol, a to ∡AXD, respektíve ∡CXY, ktoré majú 45°. Vieme si dopočítať tretí - posledný uhol trojuholníkov - keďže vieme, že súčet vnútorných uhlov v trojuholníku je 180°​. ∡XYC​ a ∡DAX​ majú teda 180°-90°-45°=45°​. Trojuholníky majú dva rovnaké 45​-stupňové uhly a preto sú rovnoramenné. Môžeme si dĺžky ich ramien označiť ako a​ a b​.

∡AXY​ tvorí spolu s ∡AXD​ a ∡CXY 180°,  keďže sú na jednej priamke, čiže ∡AXY=180°-90°-45°=90°​. Zo zadania vieme, že úsečky \overlinesegment{XY}​ a \overlinesegment{WZ}​ sú rovnobežné, čiže uhly medzi nimi a úsečkou \overlinesegment{AX} sú súhlasné, a teda zhodné. Keďže už vieme ∡AXY​ (90°)​, vieme že ∡AWZ​ je tiež 90°​. 

    Keďže ∡DAX=45°​, tak ∡XAB​ bude 90°-45°=45°​. ∡WAZ​ má teda 180°-90°-45°=45°​. Vidíme, že aj ΔWAZ​ je rovnoramenný.

\overlinesegment{AX}​ je preponou pravouhlého trojuholníka ΔAXD​. Vieme si označiť jej veľkosť ako c. Úsečku \overlinesegment{AX}​ delí bod W​ na dve polovice a \overlinesegment{AW}=\overlinesegment{WX}=\cfrac{\overlinesegment{AX}}{2}=\cfrac{c}{2}​. Nakoľko vieme, že Δ​WAZ​ je rovnoramenný, vieme že aj \overlinesegment{WZ}=c/2​. Zo zadania vieme, že \overlinesegment{WZ}=\overlinesegment{XY}​, čiže aj \overlinesegment{XY}=\cfrac{c}{2}.

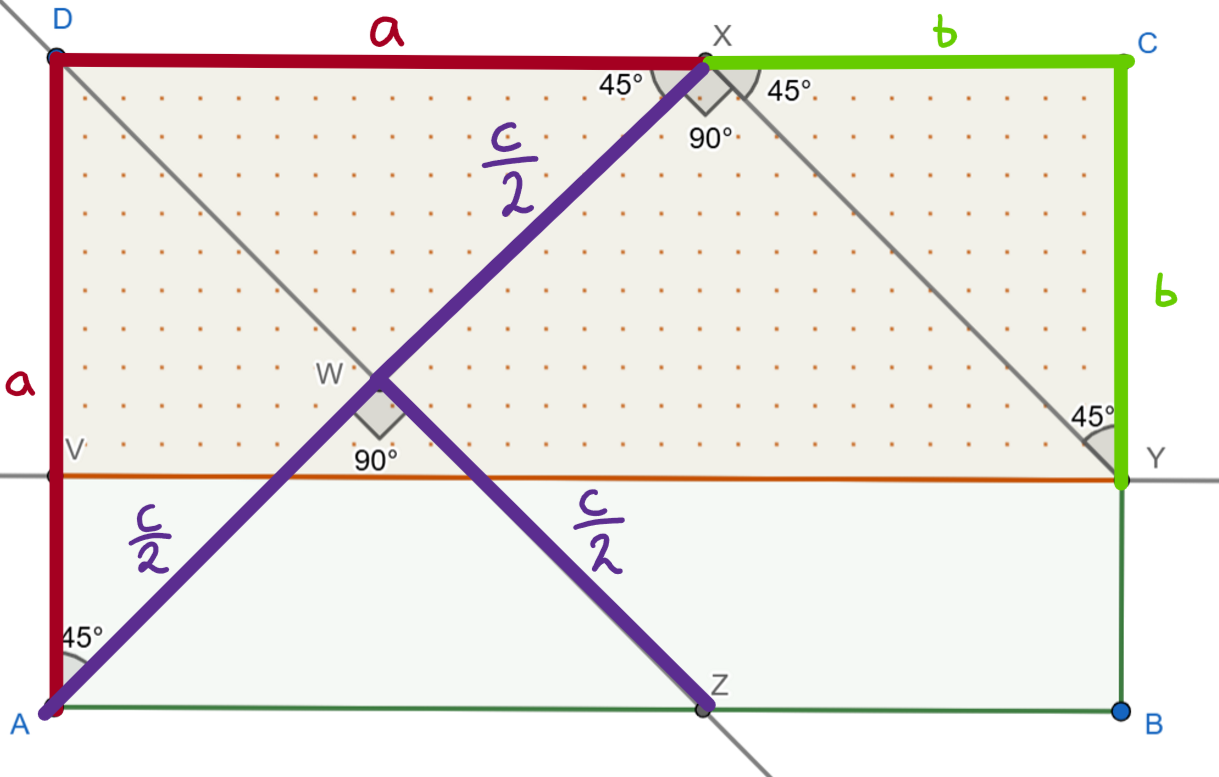
\overlinesegment{XY}​ je preponou pravouhlého trojuholníka ΔCXY​, ktorý je podľa vety uuu​ podobný Δ​ DAX​ (oba trojuholníky majú všetky uhly rovnaké). Nakoľko vieme, že prepona Δ​DAX,  \overlinesegment{AX}, je c​ a prepona
ΔCXY,  \overlinesegment{XY}, je \cfrac{c}{2}​, vieme, že koeficient podobnosti týchto trojuholníkov je 2. To znamená, že
ΔCXY bude mať všetky strany polovičné v porovnaní s Δ​DAX​. To znamená, že \cfrac{a}{2}=b​, respektíve a=2b​.

    Ako je aj z náčrtu vidieť, obsah obdĺžnika ABCD​ si vieme zapísať ako a×(a+b)​ a obsah obdĺžnika VYCD​ ako b×(a+b)​. Keď si nahradíme za všetky a​ hodnotu 2b​, zistíme, že pomer obsahov trojuholníkov je
S_{ABCD} : S_{VYCD} = 2b×(2b+b) : b×(2b+b) = 6b^2 : 3b^2 = 6 : 3 = 2 : 1​.

Obsah ABCD​ je dvakrát vačší ako obsah VYCD​.

Obrázky sú len ilustračné a nemusia nutne spĺňať všetky podmienky zadania.

Komentár

Veľa riešiteľov si nakreslilo obrázok tak, že priamo z neho vizeralo, že body V,W a Y ležia na jednej priamke. Nanešťastie zadanie hovorí iba to, že úsečka VY je rovnobežná so stranou AB. To, že na úsečke VY​ leží aj bod W bolo treba dokázať. Riešeniam, ktoré použili, že body V,W a Y sú na jednej priamke sme dávali maximálne 3 body, keďže s touto vedomosťou sa dalo už jednoducho ukázať, že pomer obsahov je 1:2. Skutočne bod W je stred úsečky AX, takže ak ním vedia úsečka VY, tak už rozdeluje obdĺžnik ABCD na polovice.​

Najprv si trošku ssprehľadníe zápis riešenia. Vytvorme si označenie MAX. Takto budeme označovať "najvyššiu početnosť nejakého znaku karty v balíčku". Teda, koľko najviac kariet rovnakého znaku sa nachádza v balíčku. Všimnime si, že keďže odoberáme karty iba po jednej, tak sa nám MAX môže meniť iba tak, že sa zníži o jedna, lebo nevieme z tohto počtu odobrať naraz viac ako jednu kartu.

Pre naše riešenie sú kľúčové dve pozorovania:

1. Ak sa nám zníži MAX​, tak v predošlom ťahu musela byť nejaká karta ostro viac početná ako ostatné.
Vieme si rozmyslieť, že toto platí, pretože karty odoberáme iba po jednom. Teda nikdy sa nemôže stať, že máme dva druhy rovnako (a najviac) početné, a potom jedným odobraním karty sa početnosti oboch z nich znížia.

2. Vždy, keď sa nám MAX zníži, tak sme uhádli znak karty.
Viem, že keď sa MAX zníži, tak to je práve vtedy, keď je jeden znak ostro viac početný ako ostatné, a teda podľa zadania hádame ju. Ak teda vytiahneme znak ktorý sme hádali, tak sme uhádli a MAX sa zníži. Ak ho nevytiahneme a neuhádli sme, tak MAX sa nezmení.

Teda, už stačí iba spojiť spojiť tieto dve pozorovania. Keďže MAX je na začiatku 13 a na konci 0​, tak sa musel 13​-krát znížiť o jedna. A teda sme určite 13​-krát uhádli.

Všimnime si, že 6-ciferné číslo môžeme zapísať ako 100000a+10000b+1000c+100d+10e+f.

Teraz sa pozrime na zvyšky tohto čísla po delení 37:

​\left(37\cdot2702 + 26\right)a+\left(37\cdot270 + 1\right)b+\left(37\cdot27 + 1\right)c+\left(37\cdot2 + 26\right)d+\left(37\cdot 2 + 10\right)e+\left(37\cdot0 + 1\right)f = 37\cdot k

Keď dáme preč všetky násobky 37​, musí byť ľavá strana stále deliteľná číslom 37​, preto dostávame:

​​26a+10b+c+26d+10e+f = 37\cdot x

A teraz keď prenásobíme túto rovnicu 26, dostaneme nasledujúci súčet:

​676a+260b+26c+676d+260e+26f = 37\cdot k \cdot26

Znovu keď sa pozrieme na zvyšky týchto čísel po delení 37 dostaneme:

26f+10a+b+26c+10d+e = 37\cdot n

Teraz k obom stranám rovnice pripočítame ten istý, šikovne zvolený násobok 37​:

​\left(37\cdot2702\cdot f+37\cdot270\cdot a+37\cdot27\cdot b+37\cdot2\cdot c+37\cdot 2 \cdot d+37\cdot0\cdot e\right)+​​

​+26f+10a+b+26c+10d+e = 37\cdot n+

+\left(37\cdot2702\cdot f+37\cdot270\cdot a+37\cdot27\cdot b+37\cdot2\cdot c+37\cdot 2 \cdot d+37\cdot0\cdot e\right)​​​

Po priamočiarej úprave dostávame:

​100000f+10000a+1000b+100c+10d+e=​​

​=37\cdot \left(n+2702\cdot f+270\cdot a+27\cdot b+2\cdot c+2 \cdot d+0\cdot e\right)​​

Všimnime si, že toto je vlastne naša pôvodná rovnica, len všetky koeficienty sú posunuté o jednu pozíciu doprava. Takto to môžeme zopakovať 6​-krát a dostaneme sa cez všetky posunutia. 

V riešení budeme používať známy fakt, že ťažnice trojuholníka sa pretínajú v jednom bode. Ďalej si označíme E a F postupne stredy strán AC a AB.

Najprv ukážeme, že body C, X, F ležia na jednej priamke. Pozrime sa na trojuholník ABC, všimnime si, že AM je jedna z ťažníc. Ďalej si všimnime, že priamka BD je tiež ťažnica, keďže uhlopriečky rovnobežníka sa rozpoľujú. Ich priesečník X je teda ťažisko ABC. Preto priamka CX prechádza stredom AB, čo je bod F.

Keďže ABCD a AYBD sú rovnobežníky, tak BC \parallel AD \parallel BY. Keďže rovnobežky BC a BY zdieľajú bod B, tak sa jedná o jednu priamku. Ďalej zo spomínaných rovnobežníkov dostávame |BC| = |AD| = |BY|, teda bod B je stred úsečky YC.

Pozrime sa na trojuholník CYD. Všimnime si, že DB je jeho ťažnica. Všimnime si, že F je stred uhlopriečky AB v rovnobežníku ABDY a teda je aj stredom druhej uhlopriečky DY. Teda CY je taktiež ťažnica v CDY. Nakoniec si spomeňme, že C,X,F ležia na priamke a teda ťažisko CDY je AM \cap CF = X. Preto aj priamka YX prechádza stredom CD, čo je N.