5. príklad - Vzorové riešenie

Existuje veľa možností, ako mohli zápasy prebehnúť, a ako hráči mohli nazbierať svojich 8, 7​, 4​ a 4​ bodov. Skúsme sa preto najprv zamerať iba na to, koľko bodov dokopy hráči môžu a potrebujú získať.

Celkový počet bodov sa zisťuje jednoducho aj preto, že v každom zápase sa udelia presne 2​ body. V prípade výhry jedného hráča dostane on všetky 2​ a v prípade remízy dostanú obaja po jednom, v súčte znova 2​. Preto ak zistíme, koľko zápasov sa odohralo, budeme aj vedieť celkový počet získaných bodov.

Počet hráčov zatiaľ nepoznáme, označme si ho teda neznámou n. Vieme, že každý z n hráčov hral n-1 zápasov (nemôže hrať sám so sebou). Vynásobením n \cdot (n-1) však zarátame každý zápas z pohľadu oboch hráčov, preto ​pre n hráčov bude \cfrac {n(n−1)}{2} zápasov.

Teda udelených bodov celkovo bude \cfrac {n(n−1)}{2}\cdot2=n(n−1)​

Keď poznáme tento jednoduchý vzorec na výpočet získaných bodov, môžeme sa postupne pozrieť na prípady s konkrétnym počtom hráčov. Pôjdeme od najmenšieho postupne smerom nahor.

​4​ hráči, ktorí sú spomenutí v zadaní, sú minimálny počet. V takom prípade je ich celkový počet bodov 8+7+4+4=23. Podľa nášho vzorca ale získajú dokopy iba 4 \cdot 3= 12 a to nie je dosť, aby každý získal svoje body. Musí ich teda byť iný počet.

Pre 5 hráčov máme podľa vzorca 5 \cdot4=20 bodov, čo stále nie je dosť ani pre prvých štyroch hráčov, ktorí získali spolu 23 bodov (alebo by piaty musel získať záporný počet bodov, čo nemôže, lebo sa dajú získavať len nezáporné počty bodov).

Pre 6 hráčov zo vzorca vychádza, že budú mať polu 6 \cdot 5=30 bodov. To by mohlo fungovať, keďže prví štyria majú 23 bodov, a zvyšní dvaja teda musia mať spolu 30-23=7 bodov. Zároveň však vieme, že ani jeden z nich nemôže mať viac ako 4 body, lebo inak by predbehli 4.​ miesto. Nemôžu mať obaja ani menej ako 4 body, lebo by získali najviac 3+3=6 bodov. Teda jeden z nich musí mať 4 body, a potom druhý musí mať 7-4=3 body.

Teraz musíme ešte nájsť riešenie, lebo to nie nutne musí existovať. Zatiaľ sme iba ukázali, aké počty bodov dosiahnu, ak existuje riešenie pre 6​ hráčov (napríklad rozloženie 10,9,5,3,2,1 nevieme dosiahnuť napriek tomu, že má správny súčet). V tomto prípade sa nám ho podarí nájsť. V tabuľke je opísané tak, že každý hráč má riadok so svojimi bodmi v stĺpci hráča, s ktorým ich získal.

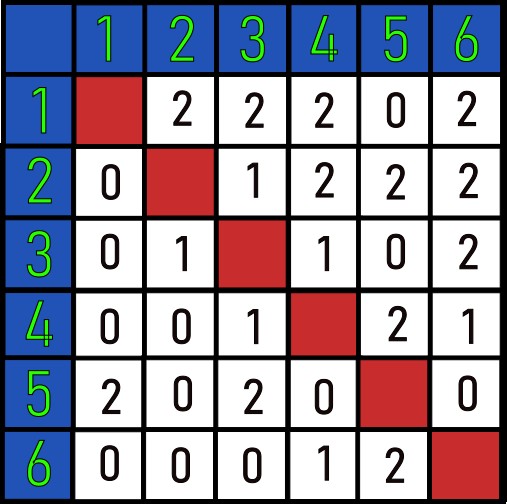
Tu však nekončíme, potrebujeme sa pozrieť, čo s možnosťami väčšími než 6​.

Pre 7 hráčov máme 6\cdot7=42​ bodov, a 3 ľudí s neznámym počtom bodov. Tí si musia rozdeliť zvyšných 42-23=19  bodov, ale každý z nich môže mať (ako sme už spomínali), len 4  body. Spolu môžu mať maximálne 3\cdot 4=12 bodov, teda to nebude vychádzať, bodov bude naopak príliš veľa.

Aj pri väčších počtoch sa nám stane, že bodov bude príliš veľa. Poďme to teda nejak dokázať, aby sme mali istotu. Pre každý o 1​ vyšší počet sa nám zväčší počet bodov, ktoré mohli získať o 4(pribudne nový hráč, ktorý môže mať maximálne 4​ bodoy). Počet bodov, ktoré si musia rozdeliť sa ale zväčší o 2\cdot n, kde n je počet hráčov bez neho (to preto, lebo on zahrá nové zápasy so všetkými hráčmi, ktoré by sa bez neho nehrali, a zápas udelí 2 body).

2n je však pre náš počet určite viac ako 4, lebo najnižšie n​ čo dosadzujeme je 7.

Teda sme dokázali, že už teraz privysoký počet bodov na rozdelenia sa vždy zvýši viac, ako sa zvýsi počet ktorí vedia získať. 

Jediný počet hráčov, pre ktorý existuje riešenie je 6, a jediná možnosť na rozdelenie bodov zvyšným hráčom je 4 a 3.​