Vzorové riešenia 1. kola

Pri takýchto úlohách je často užitočné pozrieť sa, ako si vieme inak povedať zadanie, aby nám to pomohlo v riešení.

Najprv sa zamyslime nad tým, či vieme nejak konkrétnejšie opísať situácie, keď získa Danko body:

Danko získa body keď je súčet čísiel na dvoch kockách párny. My vieme, že súčet dvoch párnych čísiel je vždy párny, súčet dvoch nepárnych čísiel je tiež párny, ale súčet párneho a nepárneho je vždy  nepárny. Vieme teda povedať, že Danko získa bod práve keď sú obe kocky párne, alebo obe nepárne.

Teraz sa pozrime na Merlina:

Merlin získa bod, keď je aspoň jedna kocka nepárna, keďže ale máme dve kocky, tak to znamená, že buď sú obe nepárne, alebo je jedna párna a jedna nepárna.

A teraz sa pozrime na Mackera:

Macker získa bod, ak je súčin párny. To sa ale nestane, ak by boli obe čísla nepárne, vtedy je súčin nepárny. Naopak, pokiaľ aspoň jedno z čísiel je párne, tak aj ich súčin je párny. Teda buď sú obe párne alebo je jedno párne a jedno nepárne.

Teraz si môžeme všimnúť, že sme každú možnosť získania bodov prepísali do podoby, kde sa len pozeráme na počty párnych a nepárnych kociek. Stačí sa nám pozerať na počty párnych, pretože tých bude 0, 1​ alebo 2​ a všetky ostatné sú nepárne (2, 1​ alebo 0​ v takom poradí). Danko získa bod, keď je 0​ alebo 2​ párnych kociek, Macker keď sú 1​ alebo 2​ párne a Merlin keď je 0​ alebo 1​ párna.

Môžeme si všimnúť, že pri každej možnosti získajú bod práve dvaja z hráčov (0​ párnych - Danko a Merlin, 1​ - Merlin a Macker, 2​ - Danko a Macker).

Ak v každom kole získajú dvaja ľudia bod, celkový súčet po 300​ kolách musí byť:
300\times2=600

Keďže teda súčet bodov Danka, Mackera a Merlina je 600​ a poznáme počet bodov Danka a Mackera, tak vieme ľahko dorátať koľko bodov má Merlin:

​600-147-226=227

Odpoveď: Merlin má 227​ bodov

Zo zadania vieme, že súčet žiadnych po sebe idúcich čísel (kľudne aj viacerých ako dvoch) nie je 3. Z toho vyplýva, že v hľadanom čísle nemôžeme mať takéto cifry:

• Tri jednotky za sebou
• Jednotku a dvojku, v tomto poradí aj naopak
• Zadanie zakazuje aj cifru 0

Zadanie hovorí, že súčet žiadnych po sebe idúcich čísel nemôže byť 3. Keď v matematike hovoríme o "nejakom počte", počet môže byť rovný aj jednej (Dokonca nevylučuje ani 0​, ani keď pri opise vecí použijeme množné číslo. Táto formulácia je však problematická, viď. komentár.). Zároveň súčet (narozdiel od sčítania) môžeme urobiť nie len viac ako dvoch, ale aj jedného čísla. Teda nemôžeme použiť ani samotnú cifru 3 - je to jedna cifra, ktorá má súčet 3. (viac na konci komentára)

Všetky ostatné čísla môžeme používať ľubovoľne, z čísel väčších ako 3 súčet 3 nedostaneme, ani z cifry 2 a inej cifry ako 1.

a)

Ak by sme použili 11 cifier 2, dostali by sme súčet čísel 11\times2=22, čo je menej ako potrebných 23. Preto tam musí byť aspoň jedna cifra väčšia ako 2.

Najmenšiu cifru väčšiu ako 2 môžem mať cifru 4 (3 nemôžeme použiť. Súčet zvyšných 10 cifier musí byť tým pádom 23-4=19. To môžeme docieliť napríklad súčtom 9 dvojok a 1 jednotky (9×2+1=19).

Teraz nám už iba stačí usporiadať 9 dvojok, 1 jednotku a 1 štvorku. Cifry 1 a 2 nesmú byť vedľa seba, aby nemali súčet 3. Bude medzi nimi štvorka - jediná iná cifra ktorú máme. Máme k dispozícii iba 1 štvorku, takže z druhej strany cifry 1 už nemôže byť nič iné ako okraj (koniec alebo začiatok) čísla. Konečné usporiadanie po dodržaní všetkých podmienok môže byť v našom prípade napríklad 14222222222.

V tejto podúlohe je viacero možností, ako mohlo číslo vyzerať, no stačí nám nájsť jednu možnosť, aby sme mohli odpovedať, že číslo mohlo mať 11 cifier.

b)

Ak by sme v tejto podúlohe skúšali nájsť číslo podobne ako v tej predošlej, rýchlo by sme zistili, že je ťažké dodržať podmienky zo zadania bez toho, aby malo číslo vyšší súčet ako 23. Preto sa môžeme zamyslieť, či to vôbec pôjde, a ak nie, tak ako by sme to vedeli dokázať. Namiesto celého 12-ciferného čísla sa najprv môžeme pozrieť na menšiu časť, a zistiť, aký najmenší súčet bude musieť mať.

Poďme dokázať, že súčet troch po sebe idúcich cifier v hľadanom čísle musí byť najmenej 6, a to tak, že vylúčime všetky menšie možnosti.

Súčet 3: Tento súčet by mohol byť najmenší možný, pretože každá cifra je aspoň 1 (1+1+1=3). Presne súčet 3 je ale zakázaný zadaním.

Súčet 4: Ak by sme chceli dostať súčet o jedna vyšší, teda 4, tak musíme jednu z cifier zvýšiť, boli by to teda 2, 1, 1. Nech ich ale ľubovoľne usporiadame, vždy bude cifra 2 vedľa aspoň jednej z cifier 1 a znova dostaneme súčet 3.

Súčet 5: Ak by bol súčet 3 po sebe idúcich cifier 5, tak bez použitia cifry 3 sa tento súčet dá vytvoriť iba ako 2+2+1. Tieto cifry tiež nevieme usporiadať bez toho, aby boli cifry 1 a 2 vedľa seba.

Súčet 6 sa už dá vytvoriť tak, aby neporušoval podmienku zo zadania a to ciframi 1+1+4=6.

Hľadané 12-ciferné číslo si vieme rozdeliť na 4 trojice po sebe idúcich cifier. Vieme, že každá táto trojica má súčet aspoň 6, inak by určite porušovala zadanie. Súčet cifier vo všetkých štyroch trojiciach teda musí byť určite aspoň 4×6=24. Tým sme dokázali, že nemôže existovať 12-ciferné číslo autobusu, ktoré má súčet cifier 23 a spĺňa zvyšné podmienky zo zadania.

Odpoveď: Číslo autobusu mohlo mať 11 cifier, ale nemohlo mať 12 cifier.

Komentár

Ospravedlňujeme sa za nie úplne jasnú formuláciu zadania ohľadom používania jednej po sebe idúcej cifry 3, a jej súčtu.Všetkým riešiteľom, ktorí správne vyriešili úlohu s používaním cifry 3, sme pôvodne udelili menší počet bodov, pretože sa tak príklad riešil výrazne ľahšie.

Táto formulácia je však problematická a myslíme si, že nemôžeme od riešiteľov vyžadovať, aby z nej správne porozumeli zadaniu. Upresnenie sme napísali do komentára, ktorý si však neprečítali všetci. Tí čo si ho prečítali však riešili náročnejšie zadanie, a nie vždy sa im podarilo ho doriešiť. Preto nakoniec všetci riešitelia dostávajú za túto úlohu 10 bodov, ak zvládli prísť k niečomu, čo je porovnateľné so správnym riešením vo verzii, kde môžeme využívať cifru 3.

Čo sa týka samotného používania spomínaných formulácií v matematike, ponúkame ešte jednu ilustráciu na príklade. Ten je omnoho jasnejší ako to, čo vzniklo v našom príklade, no ukazuje, že takúto možnosť je dobré si uvedomovať.

Pokiaľ dopredu nevieme koľko čísel budeme sčítavať, tak sa oplatí mať definované, čo znamená súčet jedného, alebo nula čísel. Často sa teda súčet nula čísel definuje ako 0 a súčet jedného čísla ako to číslo, ktoré sčítavame. Predstavme si, že čakáme kamarátov, ktorí nám prídu na oslavu a každý nám donesie niekoľko koláčov. Tak nakoniec počet koláčov bude súčet počtov, ktoré doniesli, jednotliví kamaráti. Ale čo ak nepríde žiaden kamarát? Tak ten súčet bude 0. Ak príde jeden, tak ten súčet bude toľko, koľko koláčov prinesie. Preto si treba dať pozor, čo presne súčtom myslíme.
Podobne v matematike je bežné, že ak pracujeme s množným číslom, napríklad “Nájdi všetky riešenia,” tak sa to nevylučuje s tým, že je riešenie iba jedno, alebo dokonca žiadne.

Ako prvú časť postupu si zistíme, koľko môže byť oblastí. V prvom rade si všimnime, že ak vynásobíme počet oblastí hodnotou každej oblasti (keďže v každej je rovnaká hodnota), dostaneme číslo 25​. To však znamená, že počet oblastí aj hodnota v každej oblasti musia byť delitele čísla 25​.

Tak sa pozrime na delitele čísla 25​. Sú to: 1,5,25​.

Koľko môže byť teda oblastí? No, zo zadania vieme, že iba jedna oblasť nie je možnosť. Na obrázku máme iba 12 trojuholníkov, teda ani 25 oblastí neprichádza v úvahu. Teda ostáva iba možnosť 5 - a teda vieme, že oblastí bude 5​. Zároveň si však vieme všimnúť, že ak má byť v každej oblasti rovnako veľká hodnota, a oblastí je 5​, tak v každej oblasti bude teda 25:5=5.

Teraz sa poďme pozrieť na samotnú hviezdičku.

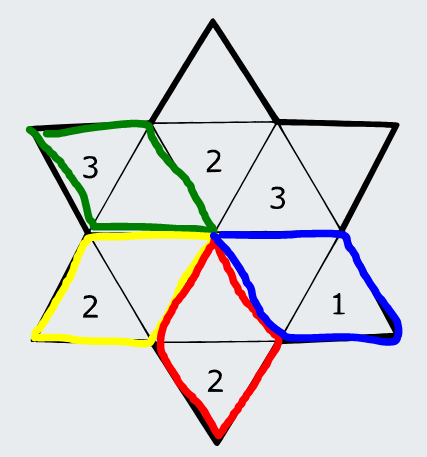
Vidíme, že ak by sme chceli hviezdičku deliť na oblasti s hodnotou päť, tieto dvojice trojuholníčkov musia určite byť spolu v nejakej oblasti. Je to preto, lebo trojuholníčky na okraji nemôžu byť v oblasti osamote, pretože by sami na súčet päť nestačili. Musíme každému z nich priradiť aspoň jeden iný trojuholník. To môže byť len jeden, ten s nimi susediaci.

Skúsme teraz pre niektoré tieto zóny zistiť, či v nejakom delení musia byť ako samotná oblasť.

Pozrime sa najprv na zelenú oblasť. V prázdnom trojuholníčku môže byť buď 1​, alebo 2​ (inak by spolu s 3-kou presiahol súčet päť). Ak by tam bola jednotka, potrebuje táto zóna ešte nejaký iný trojuholníček, aby sme ju mohli vyhlásiť za platnú oblasť pri delení. V tomto bode budeme už mať súčet 4​, teda trojhulník s dvojkou vnútri už pridať nemôžeme. Preto by sme museli pridať do tejto oblasti prázdny trojuholník zo žltej zóny, to však znamená, že by sme museli pridať žltú zónu celú. To však už nefunguje, pretože spolu s dvojkou by sme už presiahli maximálny súčet v oblasti. Teda v prázdnom trojuholníku v zelenej zóne bude určite dvojka, a vždy keď budeme podľa pravidiel deliť hviezdu na oblasti, zelená zóna na našom obrázku bude musieť byť jednou z oblastí.

Rovnaký trik vieme použiť aj na žltú zónu. Môže tu byť buď 1,2​ alebo 3​. Ak by tu bola jednotka alebo dvojka, museli by sme k tejto zóne pridať ešte nejaké trojuholníky, aby mala súčet päť. My však už vieme, že zelenej zóny sa chytať nemôžeme. Preto by sme museli zasiahnuť do červenej zóny, pridať ju celú, čím by sme už presiahli súčet päť, keďže v červenej aj v žltej zóne musí byť súčet minimálne tri. Teda v prázdnom políčku v červenej zóne bude trojka.

Tu máme teda upravenú hviezdičku:

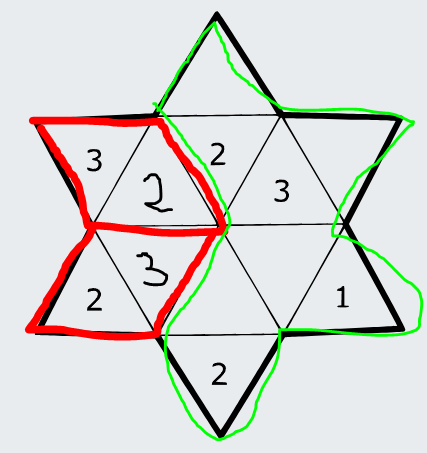
Pozrime sa teraz na zelenú zónu. Čo keby bolo nejaké políčko samotné v oblasti? To políčko by v sebe malo číslo 5​. Teda ako by potom vyzerala zelená zóna? Vieme, že v nej súčet je určite aspoň 1 +2+2+3+5=13. V prázdnych políčkach musí byť zároveň aspoň jednotka. Teda ostávajú nám ďalšie 3​ políčka, teda k súčtu 13 prirátame 3​, takže nám vyjde súčet aspoň 16​. Toto však nemôže byť, lebo v tejto zelenej zóne musíme vytvoriť práve 3​ oblasti, ktoré majú každá hodnotu 5​. My sme už však narátali súčet aspoň 16​, čo je spor. Teda nijaké políčko samostatné nebude.

Pozrime sa teraz na tieto trojuholníky:

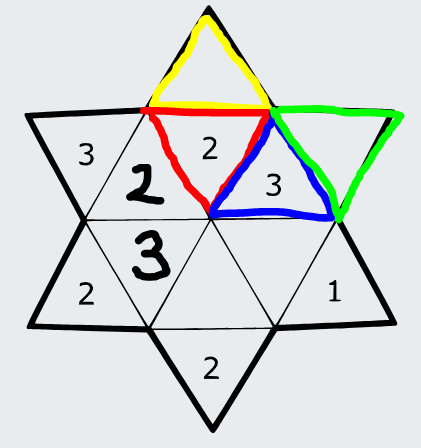
Môžeme si všimnúť, že keďže žltý trojuholník nemôže byť sám v oblasti, musí byť spolu s aspoň červeným. Nemôže však už byť aj s modrým, pretože červený a modrý dokopy by dali súčet 5​, a spolu so žltým by to presahovalo súčet 5​. Ďalšia oblasť teda bude pozostávať zo žltej a červenej zóny.

Pozrime sa teraz na zelenú zónu. Znova, vieme už, že nemôže byť v oblasti sama, teda musí byť v oblasti aspoň s modrou zónou. Z obrázka 1 jedna tak isto vieme, že ak by bola zelená zóna v oblasti aj s ďalším trojuholníkom, teda tým pod modrým, musí byť v tej istej zóne aj políčko s jednotkou. No, a to by už opäť prekročilo v súčte limit 5​, pretože by sme v tejto oblasti mali dve prázdne políčka (ktoré majú hodnotu aspoň 1​), a políčko s hodnotou 3​, a políčko s hodnotou 1​. To je 1+1+1+3 = 6, čo je viac ako povolených 5​. Teda oblasť bude pozostávať zo zeleného a modrého trojuholníka. Toto má na doplnenie iba jednu možnosť, a to, že v zelenom trojuholníku bude 2​. 

Nakoniec nám ostáva urobiť iba poslednú zónu zo zvyšných trojuholníkov. To má opät iba jednu možnosť, a to takú, že dáme do voľných trojuholníkov jednotky.

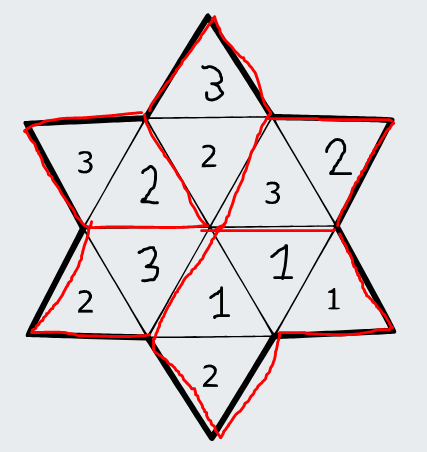
Všimnime si, že sme počas celého riešenia dopĺňali čísla, ktoré inú možnosť na doplenenie nemajú. Dokázali sme tak, že toto riešenie je jediné možné, a žiadne iné validné nie je. Toto je tiež dôležitá časť riešenia.

Experimentovaním s menšími tabuľkami (napríklad 5,7​) môžeme dostať nápad, že pre tabuľku so stranou dĺžky 2n+1​ je odpoveď n.

Túto úlohu môžeme vyriešiť tak, že ukážeme pre aké rozmery najväčšieho štvorca už úloha vyriešiť nejde. A potom nájdeme také riešnie, ktoré má štvorec len o 1​ menší. ​

Ako prvé ukážeme, že v tabuľke nemôže byť jednofarebný štvorec so stranou dĺžky väčšiou ako 1012​.

Ak by existoval červený štvorec so stranou dĺžky aspoň 1012, tak by muselo byť aspoň 1012​ stĺpcov, v ktorých je 1012 červených štvorčekov čo je väčšina. Potom by bolo najviac 2023-1012 = 1011 stĺpcov v ktorých je väčšina štvorčekov zelených, čo podľa zadania nemôže.

Ak by existoval zelený štvorec so stranou dĺžky aspoň 1012, tak by muselo byť aspoň 1012​ riadkov, v ktorých je väčšina štvorčekov zelených. Potom by bolo najviac 1011 riadkov v ktorých je väčšina štvorčekov červených, čo tiež podľa zadania byť nemôže.

Teraz ukážeme, že jednofarebný štvorec s dĺžkou strany 1011​ môže existovať. Nájdeme také ofarbenie, že v tabuľke existuje jednofarebný štvorec s dĺžkou strany 1011​.

Každému štvorčeku priradíme unikátnu dvojicu čísel i,j​, pričom i​ označuje číslo stĺpca (číslujeme zľava do prava) a j​ označuje číslo riadku (číslujeme zhora dole). Na zeleno ofarbíme práve tie políčka, pre ktoré platí jedno z nasledujúcich:

• ​​ i aj j​ sú 1012​​
• ​​ i aj j​ sú menšie ako 1012​​
• j je väčšie ako 1012​​

Takto dosiahneme, že v ľavom hornom rohu máme štvorec so stranou 1011, ktorý je celý zelený. Zároveň je v prvých 1011 riadkoch 1012 červených políčok a v strednom riadku 2022 červených políčok, takže pravidlo s riadkami sme splnili. A zas v prvých 1011 stĺpcoch máme 2022 zelených políčok a v prostrednom stĺpci máme 1012 zelených políčok, takže aj pravidlo so stĺpcami sme splnili.

Kedže tabuľka 2023 \cdot 2023 je príliš veľká aby sme ju vedeli dať do vzorového riešenia, tak na nasledujúcom obrázku je riešenie pre tabuľku so stranou 11. Veľmi ľaho si potom môžete predstaviť, že riešenie pre stranu 2023 bude vyzerať rovnako ale každý zo štvorcov v rohoch bude mať veľkost strany 1011 a stredný riadok a stĺpec budú vyzerať rovnako.​

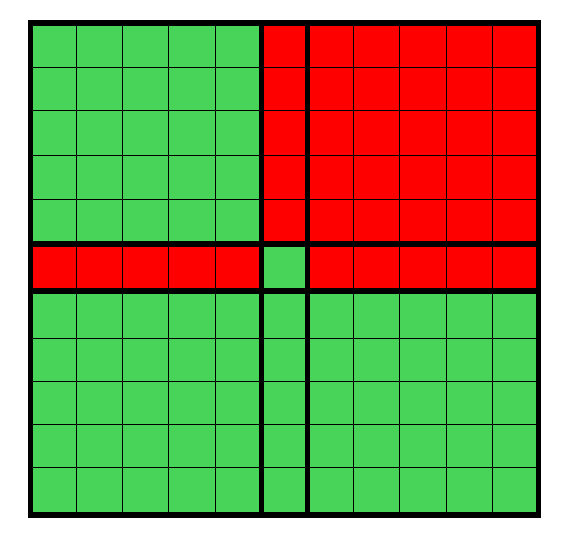
​Odpoveď: Najväčšia možná strana jednofarebného štvorca má dĺžku 1011​.

V tomto príklade v skutočnosti na veľkosti tabuľky vôbec nezáleží, ale často sa oplatí snažíť sa získať intuíciu na malých, konkrétnych prípadoch. 

Vedúci sa nevedia dostať na dve stranou susediace políčka. Je to kvôli dvom nasledujúcim faktom.

a. Nech vedúci pohnú ľubovoľnou svojou figúrkou ľubovoľným smerom, tak obchodník vie zabezpečiť, že po jeho ťahu sa figúrky budú nachádzať v uhlopriečnych vrcholoch obdĺžnika.

Všimnime si, že to na začiatku hry platí. Teraz predpokladajme, že sme v niekedy počas hry v danej pozícií a vedúci spravia ťah ľubovoľnou svojou figúrkou. Pokiaľ vedúci (modré figúrky) spravia ťah v pravo-ľavom smere. Tak obchodník sa posunie figúrkou ktorá je nad, poprípade pod vedúcim rovnakým smerom ako sa posunul vedúci. Znovu sme vytvorili obdĺžnik.

Podobne pokiaľ vedúci spravia ťah v horno-dolnom smere, tak obchodník sa posunie figúrkou ktorá je vpravo, poprípade vľavo od vedúceho, rovnakým smerom ako sa posunul vedúci.

Týmto spôsobom vieme zaručiť, že vždy keď vedúci bude na rade, tak figúrky budú tvoriť vrcholy obdĺžnika. Dokonca takého, že figúrky každej farby budú od seba uhlopriečne. 

b. Nech sú figúrky pred ťahom vedúcich vo vrcholoch dákeho obdĺžnika, tak ako vyššie. Potom vedúci nevedia spraviť krok, ktorý by im umožnil, aby sa ich figúrky stretli hranou.

Na to, aby sa jedna figúrka vedúcich dotkla hranou druhej, tak musí skončiť na rovnakom riadku, alebo stĺpci. Tým, že obchodník dopĺňa útvar do obdĺžnika, tak jedna obchodníkova figúrka blokuje vstup vedúcim do rovnakého riadka a druhá stĺpca. Takže nielen, že nebudú nikdy susediť figúrky vedúcich, dokonca sa nikdy nedostanú ani na spoločný riadok, alebo stĺpec.

Odpoveď:

Obchodník vie zaručiť, aby sa vedúci nedotkli hranou.

Ak má číslo deliteľ, existuje k tomuto deliteľu “dvojica”, s ktorou majú súčin rovný pôvodnému číslu. Zároveň čím väčší je jeden deliteľ z dvojice, tým menší je druhý, aby sme mali stále rovnaký súčin. Číslo d, ktoré povie obchodník, je najväčší deliteľ n. Teda existuje nejaké menšie (poprípade rovnaké) číslo p, pre ktoré platí:

n = d \cdot p

Vieme, že p je najmenší deliteľ n väčší ako 1 (ak p=1, tak d = n, čo podľa zadania nemôže). Pretože ak by sme namiesto p dokázali dať menšie číslo, jeho dvojička by bola väčšia ako d, ale také číslo nemáme.

Zo zadania vieme, že:

n + d = 10^{x}

Za n si dosadíme d \cdot p a rovnicu upravíme:

d \cdot p + d = 10^{x}

d \cdot (p + 1) = 10^{x}

Číslo 10^{x} si vieme prepísať ako 5^{x} \cdot 2^{x}. Čiže dostaneme:

d \cdot (p + 1) = 2^{x} \cdot 5^{x}

Keďže čísla 2 a 5 sa už nedajú rozložiť na súčin iných čísel (sú prvočísla), tak aj na ľavej strane rovnice bude musieť byť súčin x dvojok, x pätiek (kde x je kladné celé číslo alebo 0), a ničoho iného. Aj d bude preto nejakým súčinom týchto čísel.

Pozrime sa, čo by sa stalo, ak by bolo d rovné 1. Ľubovoľné n je deliteľné samým sebou a 1. Vieme teda povedať, že ak jeho najväčší deliteľ, menší ako samotné číslo, je 1, tak nemá žiadnych iných deliteľov ako seba a 1 (je prvočíslo). Dvojička k najväčšiemu deliteľovi menšiemu ako n (1), bude teda n, lebo ich súčin musí byť n. Keď toto dosadíme do rovnice, ktorú sme si odvodili:

n + 1 = 10^{x}

n = 10^{x} - 1

V tomto prípade 10^{x} - 1 musí byť prvočíslo. To avšak nikdy nemôže platiť, lebo každé takéto číslo bude deliteľné 9, keďže všetky takéto čísla sú tvaru 9999..., čo bude mať ciferný súčet 9 \cdot k pričom k je počet cifier, čo je určite deliteľné 9.

Ak d nie je rovné 1, vieme dokázať, že p musí byť menšie ako 6. Vieme totiž, že p je najmenší deliteľ n, ale aj všetky delitele d (vrátane aspoň jednej dvojky alebo päťky) sú tiež delitele n (deliteľ deliteľa je aj deliteľom pôvodného čísla). Preto aby p ostalo najmenšie, musí byť najviac 5.

Vyskúšajme teda všetky možnosti pre p: (2, 3, 4 a 5):

Ak p = 2, tak potom (p+1) = 3, teda súčin d \cdot (p+1) by bol deliteľný 3, čo mocnina desať byť nemôže.

Ak p = 3, tak potom (p+1) = 4, teda platí:

d \cdot 4 = 10^{x} = 2^{x} \cdot 5^{x}

Zároveň d nemôže byť deliteľné 2, keďže najmenšie prvočíslo v rozklade n je 3 a d je súčinom nejakej jeho časti. Z toho vyplýva, že jediná časť súčinu na pravej strane obsahujúca dvojky je 4. A teda platí 4 = 2^{x}. Teda x = 2. Dosadíme naspäť:

d \cdot 4 = 100

A teraz už vieme, že v tejto možnosti d = 25 a n = d \cdot p = 75, čo je zároveň vyhovujúce n.

Ak p=4, tak potom aj číslo 2 je deliteľ n, pretože 2 je deliteľom p. p by teda nebolo najmenším deliteľom n.

Ak p = 5, tak potom (p+1) = 6, teda súčin d \cdot (p+1) by bol deliteľný 3, čo mocnina desať byť nemôže.

Odpoveď:  n = 75

Keď obchodník zamieša karty, nevieme, ktorá je ktorá. Môžeme sa ale pozrieť na niektoré z nich znova a tým zistiť, ako ich zamiešal. Tie, na ktoré sa pozrieme síce potom zamieša znova a teda o nich veľa vedieť nebudeme, ale dozvieme sa, ktoré karty sú tie, na ktoré sme sa pozreli prvýkrát a nie druhýkrát.

Príklad

​n = 4;k = 3​​

Na začiatku napríklad otočíme tri karty takto:

Teraz ich obchodník nejako zamieša a vráti naspäť.

Teraz vieme, že prvé tri karty sú 1, 2​ a 3​, nevieme však, ktorá je ktorá. Otočíme ďalšie tri karty:

Teraz vieme, ako obchodník zamiešal prvé tri karty - trojku položil na druhé miesto, jednotku na prvé a teda dvojku musel položiť úplne vľavo.

Teraz obchodník karty 1, 3​ a 4​ zamiešal, takže nevieme, kde je tá štvorka, trojka a jednotka. Stále ale vieme, že karta najvac vľavo je dvojka.

Takto môžeme otočiť ďalšiu a ďalšiu trojicu až do poslednej. Tým budeme presne vedieť, čo je na prvých piatich kartách. Keďže máme iba čísla 1 - 4​, musí byť medzi nimi aspoň jedna dvojica rovnakých kariet. Potom môžeme proste otočiť tie dve (s ľubovoľnou ďalšou) a máme zaručene dvojicu rovnakých.

Pre všeobecné n, k​​

Na začiatku otočíme prvú až k-tu kartu, potom druhú až k+1-vú, ... až posledných k​. Budeme teda vedieť, aké číslo je na prvých 2n-k kartách. Pre k \lt n​ platí n-k \gt 0​ a teda 2n - k \gt n​. Teda vieme, aké číslo je na viac ako n kartách. Je ale iba n rôznych čísel a teda na aspoň dvoch z nich sú rovnaké čísla. Ukážeme teda na tie dve (a ešte hocijaké ďalšie) a vieme, že je tam dvojica rovnakých.

Jediný prípad, kedy toto nefunguje je pre n=k​. Vtedy totiž budeme mať informáciu iba o n​ kartách a teda medzi nimi nemusí byť žiadna dvojica. Pozrime sa teda na tento prípad podrobnejšie:

Pre k=n​​

Môžeme skúšať rôzne stratégie pre vedúcich, ale žiadna nevyzerá, že funguje. Tak poďme skúsiť dokázať, že ak obchodník namiešava karty správne, vedúci môžu otáčať donekonečna a nikdy sa im nepodarí otočiť dve rovnaké.

Keď k=n​, jediný spôsob ako môžu neotočiť dve rovnaké je otočiť jednu jednotku, jednu dvojku, ... až jedno n. Takže vlastne dokazujeme, že obchodník vždy vie namiešať karty tak, aby otočili jednu z každej.

Vedúci môžu postupne získavať nejaké informácie o niektorých kartách. Tak sa pozrime na ten príklad, keď majú najviac informácií, ako môžu mať - vedia, aké čísla sú na všetkých kartách okrem tých, ktoré otočili v poslednom ťahu (tie totiž obchodník mohol zamiešať a môžu byť hocijako). Keďže v poslednom ťahu museli otočiť jednu jednotku, jednu dvojku..., tak tie ostatné (o ktorých vedia) sú tiež jedna jednotka, jedna dvojka, ... Vyzerá to teda nejako takto:

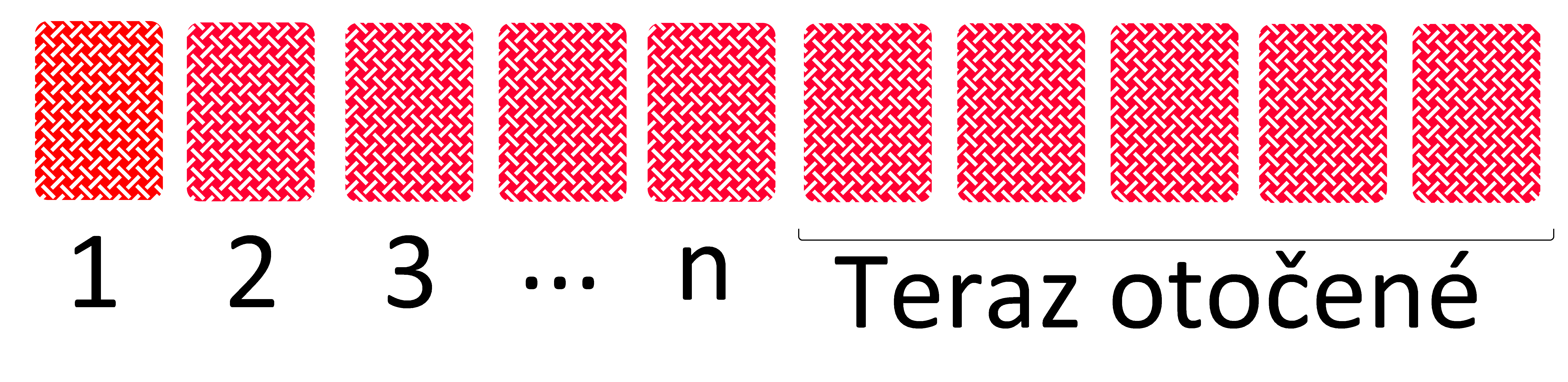
Vedúci teraz otočia niektoré z kariet, ktoré poznajú (ako si vyberú) a "naslepo" nejaké z tých, ktoré boli teraz otočené. Môže sa však stať, že z nich nešťastnou náhodou otočia práve tie, ktoré nevybrali z tých, ktoré poznajú (napríklad ak z tých, ktoré poznali vybrali jednotku a dvojku, tak sa im môže stať, že z tých ostatných vyberú práve 3, 4, ..., n​. Tým sa zasa dostanú do takej istej pozície (majú informácie najviac o n​ kartách) a toto isté sa môže zopakovať znova a znova. Vždy môžu mať smolu a otočiť presne jednu z každej karty. Teda pre k=n​ nevedia s istotou po žiadnom počte ťahov otočiť dve rovnaké.

Odpoveď:

Keď 2 \le k \lt n, vedia vedúci ukázať na dvojicu rovnakých. Keď k=n​, vie im obchodník zamiešavať karty tak, že dvojicu nikdy neotočia

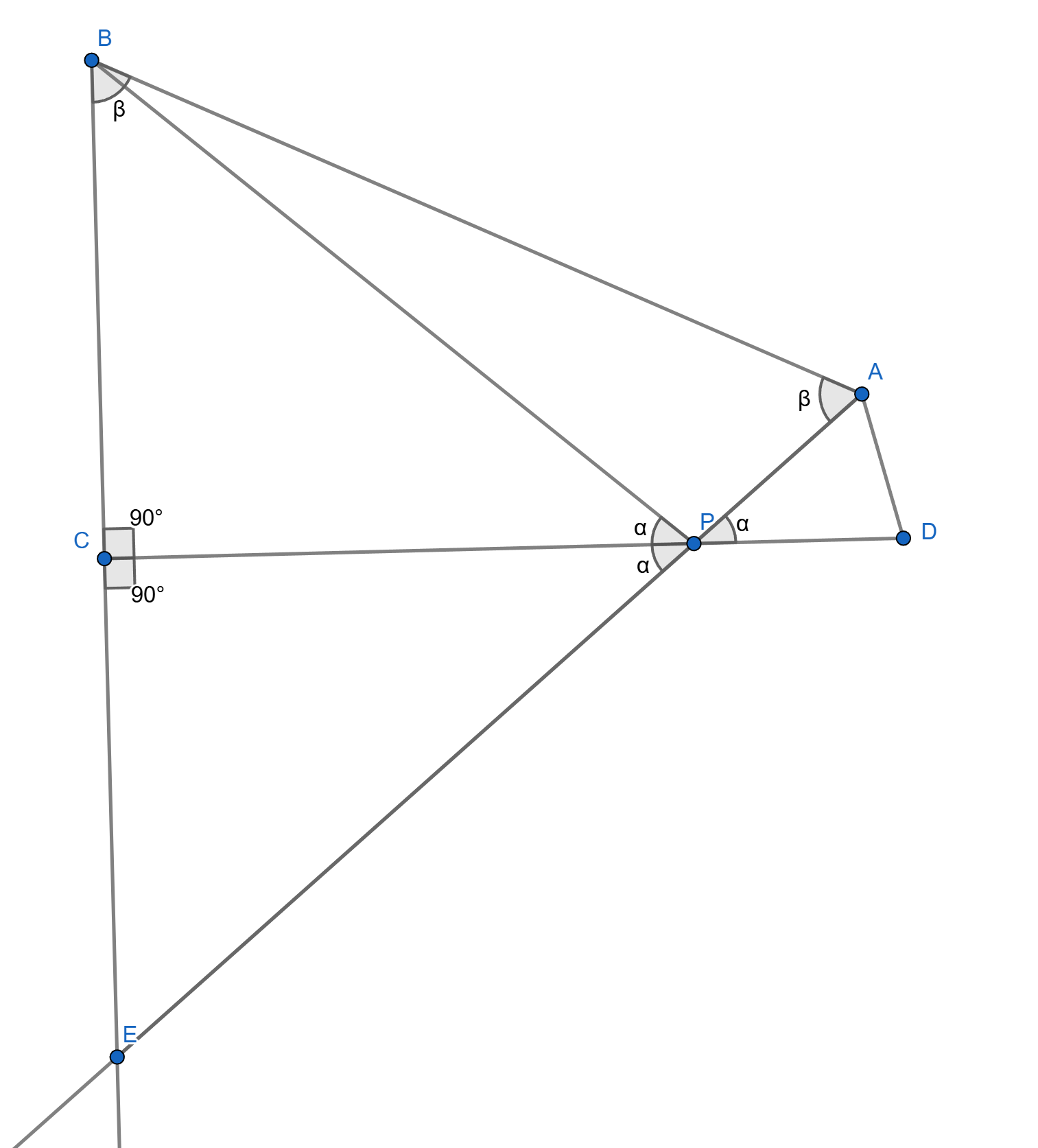
Táto úloha sa dala vyriešiť nasledovným spôsobom:
Označme si uhol \vert \measuredangle DPA \vert= \vert \measuredangle BPC \vert= \alpha, \vert \measuredangle ABC \vert= \vert \measuredangle PAB \vert= \beta. Najprv dokážme že musí platiť \beta \lt 90:

Pozrime sa na štvoruholník ABCP, vieme že súčet jeho vnútorných uhlov musí byť 360. Preto musí platiť:

​\vert \measuredangle CPA \vert+ \beta + \beta + 90 = 360

Vieme, že \vert \measuredangle CPD \vert= 180 keďže P​ leží na \overline{CD}​, a \vert \measuredangle DPA \vert= \alpha,  preto \vert \measuredangle CPA \vert= 180 - \alpha aby sa to dokopy rovnalo 180. Dosadíme:

\begin{aligned} 180-\alpha + 2\beta +90 &= 360 &&/ - 270 \\2\beta - \alpha &= 90 &&/ + \alpha - 90 \\2\beta - 90 &= \alpha \end{aligned}

Ak by bolo \beta \geq 90 tak platí 2\beta \geq 180, 2\beta - 90\geq 90 \implies \alpha \geq 90. To by znamenalo že 2\alpha \geq 180, a keď sa pozrieme na uhol \vert \measuredangle CPD \vert, všimneme si že to je 2\alpha + \vert \measuredangle APB \vert= 180 keďže ​​2\alpha \geq 180 tak to znamená že \vert \measuredangle APB \vert\leq 0, záporný uhol neexistuje, a keby to bolo 0​ tak by to znamenalo že ide o zdegenerovaný štvoruholník, ktorý nedovoľuje zadanie.

Takže \beta \lt 90, čo znamená že môžeme predĺžiť priamku \overleftrightarrow{BC} a \overleftrightarrow{AP}, a určite sa pretnú, a ich prienik označím E. ​

Podľa vrcholových uhlov platí \vert \measuredangle DPA \vert= \vert \measuredangle EPC \vert= \alpha, a keďže

\begin{aligned} \vert \measuredangle BCE \vert&= \vert \measuredangle BCP \vert+ \vert \measuredangle PCE \vert&&= 180 \\\vert \measuredangle BCE \vert&= 90 + \vert \measuredangle PCE \vert&&= 180 \\\vert \measuredangle PCE \vert&= 90 \end{aligned}

Podľa vety USU musí teda platiť zhodnosť trojuholníkov \triangle BPC \text{ a } \triangle CPE,  lebo majú rovnaký uhol pri P​, pri C​ a rovnako dlhú stranu medzi nimi(PC)

Keďže sú zhodné, tak sa \vert EP \vert = \vert PB \vert, čo znamená že \triangle BEP je rovnoramenný. Všimnime si, že \vert AE \vert = \vert AP \vert + \vert EP\vert , a \vert EP \vert = \vert PB \vert, znamená to že \vert AE \vert = \vert AP \vert + \vert PB \vert.

​ABE je rovnoramenný s ramenami \overline{AE} a \overline{BE}, keďže uhly pri A a B sú zo zadania rovnaké.

Z toho dostávame že \vert BE \vert = \vert AP \vert + \vert PB \vert. Keďže sú \triangle BCP \text{ a } \triangle PCE zhdoné, tak rozdeľujú \overline{BE} na polovicu, z čoho dostávame že \vert BC \vert = \vert CE \vert = \frac12\vert BE \vert, dosadíme:

​\vert BC \vert = \frac{\vert AP \vert + \vert BP \vert}{2}

A tým sme dokázali úlohu.

a)

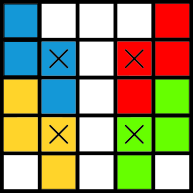
Keď sa snažíme dávať S tetrominá do tabuľky 5\times5​, nepodarí sa nám ich umiestniť viac ako 4. A to aj napriek tomu, že nám ešte ostali voľné políčka. Môžeme si všimnúť, že keď ľubovoľne umiestnime 4​ tetrominá, tak niektoré políčka budú vždy zabraté. Sú to tieto políčka:

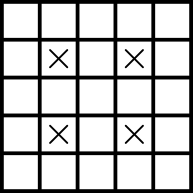
​A nebola to iba náhoda. Keby sme odstránili tieto políčka, do tabuľky by sa nezmestilo ani jedno tetromino. Inak povedané, každé tetromino musí obsahovať niektoré z týchto políčok. Keďže v tabuľke 5 \times 5​​ existujú 4​ takéto políčka, môžeme tam zmestiť najviac 4​ tetrominá. To sa nám aj podarí a tabuľka môže vyzerať napríklad takto:

c)

Rovnako ako v tabuľke 5\times5​, aj v tabuľke 7\times7​ chceme nájsť čo najmenej políčok bez ktorých nedokážeme umiestniť žiadne tetromino. Keď ich nájdeme n​ tak vieme, že tetromín sa tam zmestí najviacn​. V tabuľke 7\times7​ existuje 9​ takýchto políčok (označených x). Ale ako vieme, že sa tam naozaj zmestí až 9​ tetromín? Stačí, keď nájdeme príklad umiestnenia deviatich tetromín do tabuľky. Tabuľka 7\times7​ vyplnená 9​ tetrominami môže vyzerať napríklad takto:

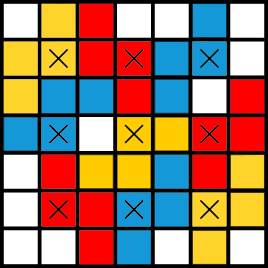
Vieme, že tetromín sa tam zmestí najviac 9​. Zároveň sa nám tam podarilo všetkých 9​ umiestniť. Odpoveď je teda 9​.

b)

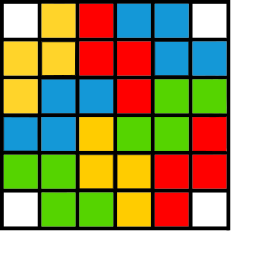
V tabuľke ​ je 36​ políčok. Teoreticky by sa tam teda zmestilo 36:4=9​ tetromín. To by ale znamenalo, že každé políčko v tabuľke musí byť využité. To znamená, že zabraté musí byť aj políčko v ľavom hornom rohu. Umiestnime tam teda zelené tetromino. Môžeme ho umiestniť tak, aby smerovalo doprava alebo nadol. Je to ale jedno, pretože nám vznikne rovnaká situácia, iba preklopená. Tak či tak nám vznikne jedno políčko pri kraji, na ktoré vieme tetromino umiestniť iba jedným spôsobom. V našom prípade to je modré tetromino ako na obrázku. Teraz ale na políčko označené krížikom nevieme umiestniť žiadne tetromino.

Týmto sme ukázali, že keď sa snažíme pokryť všetky políčka, určite sa nám to nepodarí. To znamená, že do tabuľky 6\times6​ sa nezmestí 9​ tetromín. Najviac teda vieme umiestniť 8​ tetromín, čo môže vyzerať napríklad takto:

​

Odpoveď:

a) Do tabuľky 5\times5​ sa zmestia najviac 4​ tetrominá.

b) Do tabuľky 6\times6​ sa zmestí najviac 8​ tetromín.

c) Do tabuľky 7\times7​ sa zmestí najviac 9​ tetromín.​​

Najprv si premyslime hornú hranicu, teda zistime, ktoré čísla v množine určite nebudú. Na "začiatku" v množine máme čísla ​0, m, n a m-n. Všimnime si, že všetko sú to čísla v tvare im+jn pre nejaké celé koeficienty i,j. No a takýto tvar budú mať aj všetky čísla, ktoré z nich vyskladáme povolenými pravidlami:

• ak sa v množine nachádza a, tak aj -a sa v nej nachádza, no a toto číslo očividne vieme vyjadriť v správnom tvare: ak a=im+jn, potom -a=(-i)m+(-j)n
• ak sa v množine nachádza a,b,a-b, potom je tam aj a+b, no a keďže a aj b vieme vyjadriť ako nejaké a=im+jn a b=km+ln, tak potom vieme vyjadriť aj a+b=(i+k)m+(j+l)n

Vidíme teda, že naozaj, v množine vieme mať iba čísla tvaru im+jn, teda súčet nejakých násobkov m a n.

Ihneď si môžeme položiť otázku: dajú sa skutočne vyskladať všetky takéto čísla? Odpoveď je taká, že áno. Spravíme to nasledovne:

• Samozrejme, máme čísla m, n, m-n a 0. Máme aj -m, -n a -(m-n)=n-m, a podľa švrtého pravidla vyskladáme aj m+n a jeho zápor -m-n.​
• vieme vyskladať všetky násobky m. Ako? Najprv využijeme fakt, že máme číslo m, a máme aj číslo m-m=0, teda vieme vyskladať číslo m+m=2m. Podobne vieme pokračovať k vyšším kladným násobkom: máme číslo 2m, m a 2m-m=m, teda vyskladáme 2m+m=3m. A tak ďalej, pre každé ďalšie x: už máme xm, m​ aj xm-m=(x-1)m, teda vieme spraviť aj xm+m=(x+1)m. Zároveň ku každému tomuto kladnému násobku v množine bude aj násobok záporný, a nulu máme už od začiatku. Teda máme všetky násobky m.
• teraz skúsme spraviť niečo podobné, ale pre čísla tvaru im+n, teda násobky m zvýšené o n. Už máme -m+n, n aj m+n, teda použime podobný postup ako naposledy: máme m+n, m aj (m+n)-m=n, teda zostrojili sme (m+n)+m=2m+n. A tak ďalej, máme xm+n, m​, (xm+n)-m=(x-1)m+n, teda získali sme (xm+n)+m=(x+1)m+n. No a záporné násobky tentokrát nemôžeme dostať tak jednoducho, pretože z n by sa stalo -n, vieme ale spraviť toto: máme -m+n, -m, (-m+n)-(-m)=n a teda dostaneme (-m+n)+(-m)=-2m+n, a tak ďalej, z -xm+n, -m, (-xm+n)-(-m)=-(x-1)m+n dostaneme (-xm+n)+(-m)=-(x+1)m+n...
• dobre, už máme všetky možné im+jn, pokiaľ j je 0 alebo 1. Ako vyskladáme všetky ostatné? Pre všetky i vieme spraviť toto: máme už im aj im+n, tak teda opäť opakujeme podobný postup, ako doteraz: máme im+n, n aj (im+n)-n=im, teda máme aj (im+n)+n=im+2n, a tak ďalej, z im+xn, n a (im+xn)-n=im+(x-1)n dostaneme (im+xn)+n=im+(x+1)n. A ako dostať im+jn kde j je záporné? Mohol by som takýto postup rozpísať ešte raz, ale nechce sa mi :) takže proste stačí povedať: máme všetky čísla tvaru im+jn kde j je nezáporné, tak ich proste znegujeme a dostaneme aj tie, kde j je záporné.​

Teda ukázali sme, že vieme dostať všetky čísla tvaru im+jn, a zároveň, že žiadne iné. Teda množina S musia byť práve tieto čísla a žiadne iné.

Ak chceme byť konkrétnejší, dá sa povedať, že sú to práve násobky najväčšieho spoločného deliteľa m,n. Naozaj - takzvaná Bézoutova identita hovorí, že NSD sa v takomto formáte vždy dá zapísať, no a to, že všetky jeho násobky (a žiadne iné čísla) sú v tvare im+jn je veľmi jednoduché ďalej dokázať :).

Poznámka k zadaniu:

Ospravedlňujeme sa, zadanie tejto úlohy bolo trochu nesprávne (ale našťastie ho všetky vaše riešenia pochopili správne). Hovorí sa tam, že treba nájsť všetky množiny S, ktoré spĺňajú dané podmienky. Týchto je omnoho viac než len táto jedna, ktorú sme my našli - napríklad aj množina všetkých celých čísel ich spĺňa (vyskúšajte si to)! Avšak zamýšľaným riešením je len táto jedna množina, kde sú len tie prvky, ktoré sa dajú týmito pravidlami z pôvodných štyroch vyskladať (to je niečo iné, než ľubovoľná množina, ktorá ich spĺňa...).