6. príklad - Vzorové riešenie

Túto úlohu niektorí z riešiteľov pochopili tak, že je 7 \times 7​ križovatiek a kraje sú od seba vzdialené 6 podchodov. Zamýšľané, bolo že je ​6\times6 križovatiek a kraje sú vzdialené 5 podchodov. Keďže zadanie v tomto nebolo úplne jasné a riešenie sa hľadalo rovnako v oboch veziách, obe sme nakoniec uznávali ako správne. Vo vzorovom riešení sa však pozrieme iba na tú prvú, postupne po podúlohách.

Podúloha a)

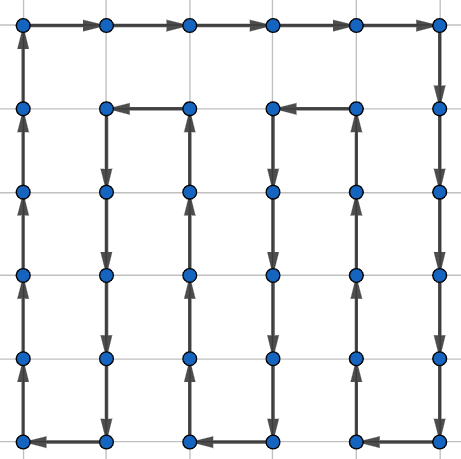
V tejto podúlohe môžme navrhnúť podchody napríklad tak ako na obrázku, že cez všetky križovatky pôjde slučka. Je jedno, ako nasmerujeme ostatné podchody, všade sa dá dostať ak pôjdeme po tejto slučke.

Podúloha b)

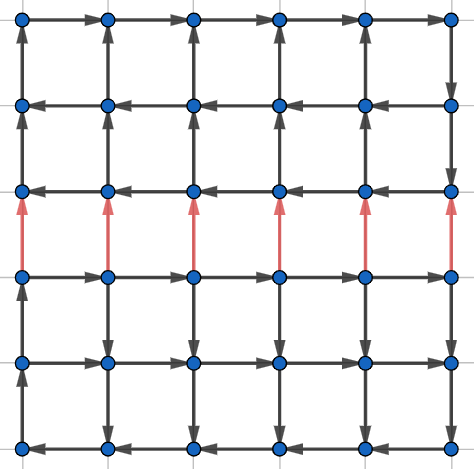
V tejto podúlohe išlo o to, či sa vždy, keď z každej križovatky vychádza aj vchádza podchod, dá dostať odvšadiaľ všade. Ak by teda existovalo rozmiestnenie, kde síce z každej križovatky vychádza aj do každej vchádza podchod, ale nedá sa dostať odvšadiaľ všade, odpoveď na b) bude nie. Jedno z takých rozmiestnení je to na obrázku. V tomto rozložení síce z každej križovatky vychádza podchod aj do každej vchádza, ale z hornej polovice obrázka sa do dolnej nedá dostať.

Podúloha c)

Na to, aby sme vždy prešli cez najviac dva zbytočné podchody je možné použiť napríklad rozloženie na obrázku. Bolo ale naozaj ťažké nájsť toto alebo iné správne riešenie a dokázať jeho správnosť bez manuálnej kontroly veľkého množstva ciest. Preto sme sa nakoniec rozhodli nedávať za túto podúlohu body a namiesto toho dať viac bodov za ostatné podúlohy.

Podúloha d)

Potrebujeme zistiť, či sa podchody dajú navrhnúť s podmienkou, že sa všade dá dostať na jeden zbytočný podchod. Najprv sa zamyslime, či nejakú časť rozmiestnenia nevieme určiť naisto, takú bez ktorej by rozmiestnenie isto nespĺňalo podmienku. Je jasné, že z rohu musí jeden podchod vychádzať a jeden doň prichádzať. Keby totiž oba vychádzali alebo vchádzali, nedalo by sa vojsť alebo vyjsť. Je jedno, ktorý z nich bude ktorý, lebo môžme tabuľku po uhlopriečke preklopiť a dostaneme tým tú druhú situáciu. Nakreslime si teda roh s týmito dvoma podchodmi. Zároveň si označme križovatky písmenami a číslami aby sa o nich ľahšie písalo.

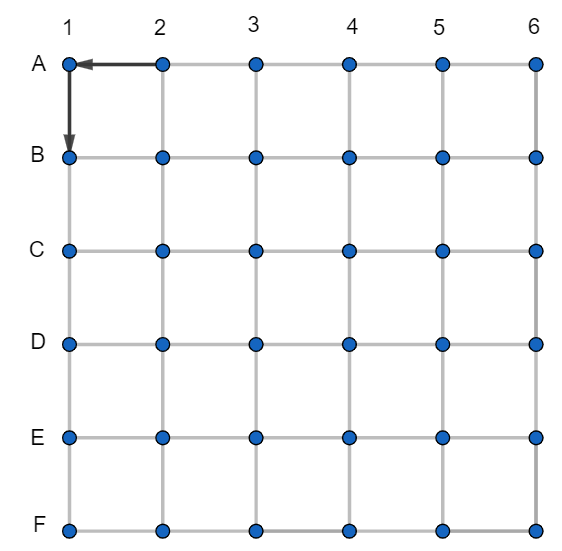
Teraz je len jedna trasa, ktorou sa dá dostať z B1 do A1 na najviac jeden zbytočný podchod - doprava, hore a doľava. Ak teda nechceme porušiť podmienku, musia tam byť podchody tak, ako na obrázku.

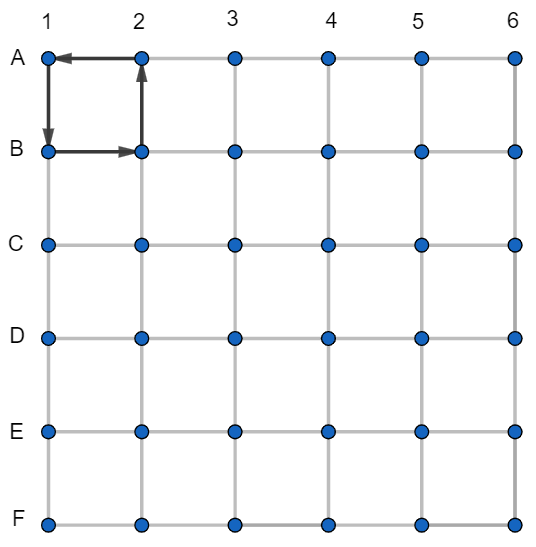
Ak by viedol podchod z B1 do C1, tak potom by sa naspäť, z C1 do B1, nedalo dostať kratšou cestou ako cez C2, B2, A2 a A1 - na dva zbytočné podchody. To by teda nebolo dobré rozloženie a tak musí viesť podchod naopak - z C1 do B1.

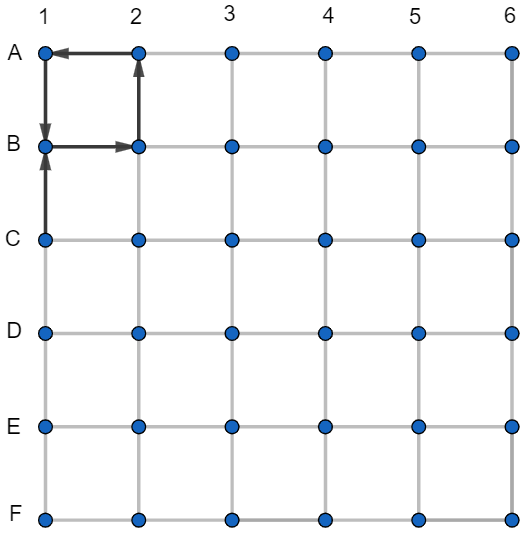
Podobne, ako pred chvíľou z B1 do A1, jediná možná cesta z B1 do C1 s najviac jedným zbytočným podchodom je cez B2 a C2, preto tam musia byť podchody ako na obrázku.

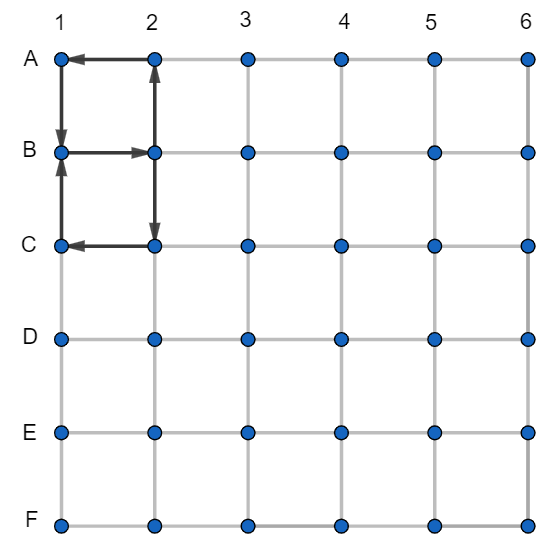
Ak by viedol podchod z D1 do C1, nedalo by sa prejsť na 1 zbytočný z C1 do D1. Preto pôjde podchod z C1 do D1.

A teraz, podobne ako už dvakrát predtým, aby sa dalo dostať z D1 do C1, musia viesť podchody takto:

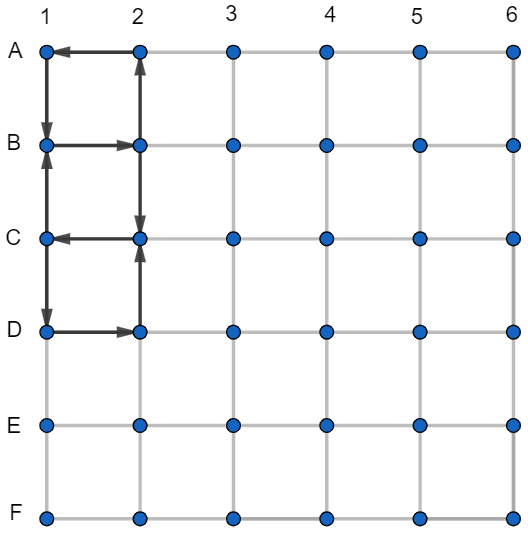
Ak by viedol podchod z D1 do E1, nedalo by sa dostať z E1 do D1 na najviac jeden zbytočný podchod. Preto musí viesť z E1 do D1.

Teraz si ale skúsme nájsť cestu z A1 do E1. V prvom kroku musíme ísť dole, v druhom doprava, čo je prvý zbytočný podchod. Ak teda chceme prejsť iba s jedným zbytočným podchodom, musíme sa odtiaľto už stále približovať. Ešte tri kroky sa nám to môže (práve jedným spôsobom) podariť - pôjdeme na C2, C1 a D1. Odtiaľ ale môžme ísť iba doprava, čím naberieme druhý zbytočný podchod.

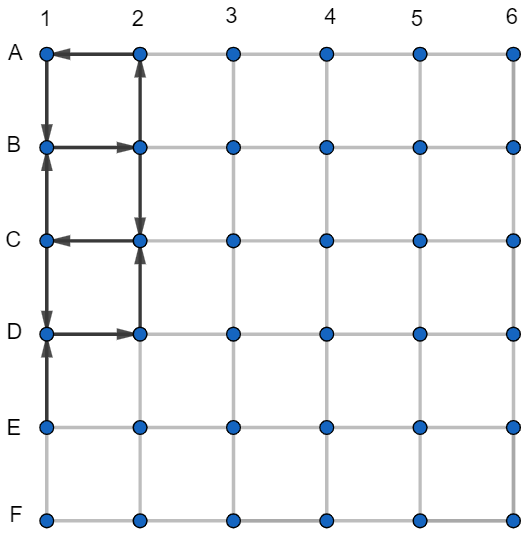
Ako sme už vysvetlili, rozloženie ku ktorému sme sa dostali, musí byť takto alebo osovo preklopené súčasťou každého rozdelenia, ktoré spĺňa podmienku v d). Aj tu však vidíme, že podmienky splnené nebudú a tak nemôžu byť splnené v žiadnom rozložení.

​Odpoveď: Pre a) sme našli fungujúce rozloženie, v b) sme našli prípad, ktorý to vyvracia, c) sa urobiť dalo, a v d) sme ukázali, že sa také rozloženie nájsť nedá.