7. príklad - Vzorové riešenie
Zadanie
Majme lichobežník ABCD so základňami AB a CD. Na strane AB si zvolíme body P a Q (v tomto poradí) tak, aby |AP| = 2 a |PQ| = |QB| = 1. Priesečník uhlopriečok štvoruholníku CDPQ označme X. Ďalej vieme, že obsah trojuholníka DPX je 1 a obsah CQB je 2. Aký je obsah celého lichobežníka ABCD?
Vzorové riešenie
Túto úlohu vieme vypočítať zistením obsahu všetkých častí lichobežníka a následným sčítaním týchto čatí (viď obrázok).
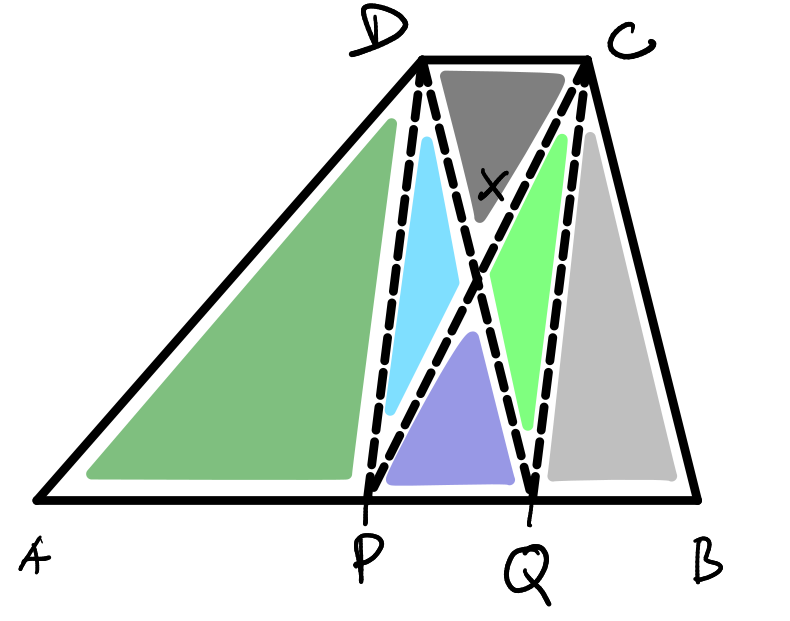
Zatiaľ však nemáme potrebné informácie na to, aby sme také vedeli spraviť, poďme teda poskúšať, čo všetko vieme z informácií v zadaní.
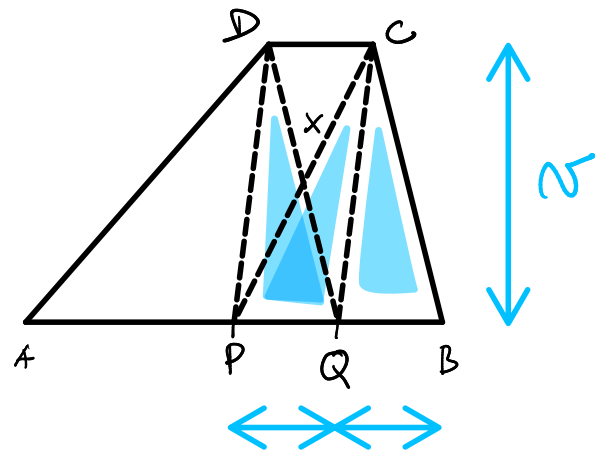
Trojuholník PQC má rovnaký obsah ako trojuholník QBC keďže majú rovnako dlhú stranu, lebo |PQ| = |QB| = 1, a výška na túto stranu je prakticky pre oba trojuholníky zhodná s výškou lichobežníka. To isté platí aj pre trojuholník PQD. Takže S_{QBC} = S_{PQC} = S_{PQD} = 2.
Taktiež si vieme vypočítať výšku lichobežníka v z obsahu jedného z týchto trojuholníkov napríklad PQD:
S_{PQD} = \frac{|PQ| \cdot v}{2}
2 = \frac{1\cdot v}{2}
v=4
Trojuholník APD má dvakrát väčšiu stranu ako trojuholník QBC ale rovnakú výšku, keďže |AP| = 2 a |QB| = 1, čo znamená, že má dvakrát väčší obsah: S_{APD} = 2 \cdot S_{QBC} = 4.
Vieme, že S_{DPX} = 1 a S_{PQD} = 2. Keďže S_{PQD} = S_{DPX}+S_{PQX}, tak z toho vyplýva, že S_{PQX}= 1 a analogicky aj S_{QCX} = 1. Zakreslime si to do obrázka.
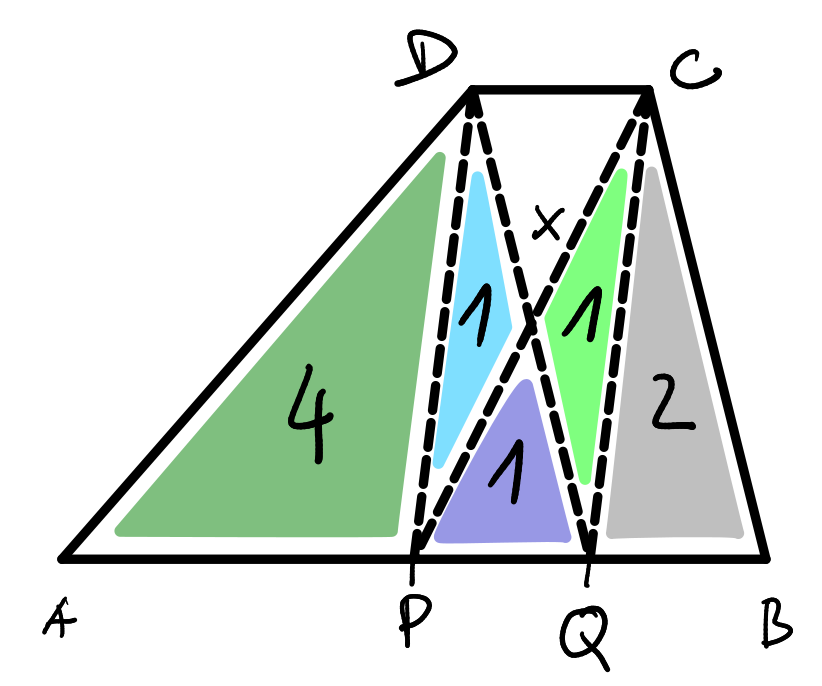
Zostala nám posledná časť, a to trojuholník DCX. Nevieme o ňom ani výšku, ani stranu.
Poďme sa teda nejako zamyslieť, ako vieme vypočítať obsah trojuholníka DCX
Obsah trojuholníka DCX vypočítame nasledovne S_{DCX} = \frac{c \cdot v_c}{2}. Ak vieme výšku celého lichobežníka, vedeli by sme od nej odčítať výšku trojuholníka PQX a potom by sme dostali v_c (viď obrázok).
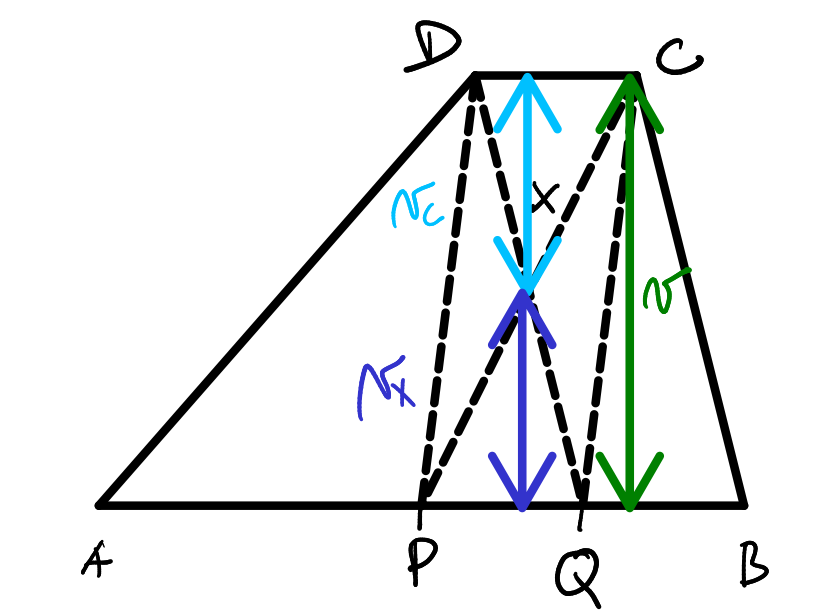
Výšku trojuholníka PQX vypočítame vďaka tomu, že vieme obsah a stranu tohto trojuholníka:
S_{PQX} = \frac{|PQ| \cdot v_x}{2}
1 = \frac{1 \cdot v_x}{2}
2 = v_x
A teda výšku v_c nášho trojuholníka DCX vypočítame odčítaním od výšky lichobežníka v=4, ktorú sme si vypočítali vyššie:
v_c = v - v_x
v_c = 4-2 = 2
Vidíme, že trojuholníky DCX a PQX majú zhodné výšky.
Čo je ďalej na týchto trojuholníkoch zaujímavé, sú ich uhly.
Vrcholové uhly budú zhodné:
|\measuredangle PXQ| = |\measuredangle DXC|
A takisto aj striedavé uhly budú zhodné:
|\measuredangle QPX| = |\measuredangle DCX|
|\measuredangle PQX| = |\measuredangle CDX|
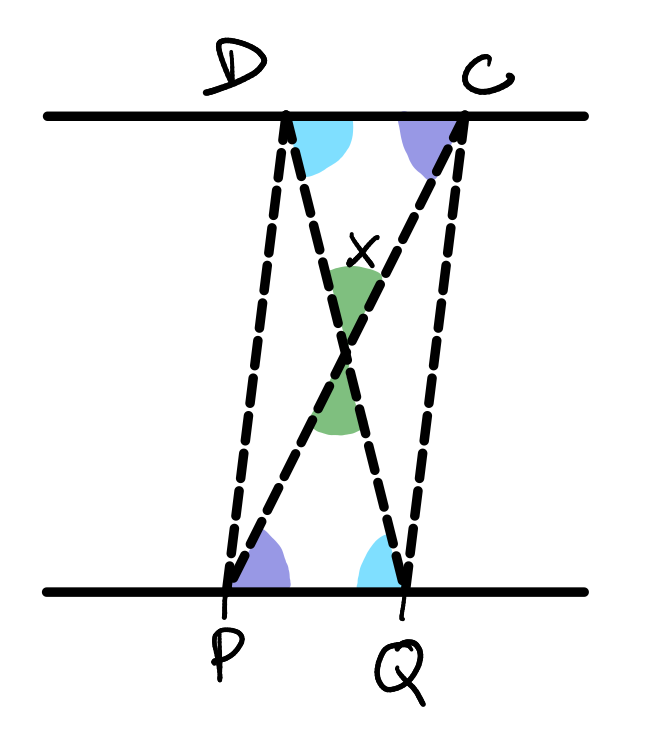
Z toho vyplýva, že trojuholníky DCX a PQX sú podobné, no zároveň majú rovnakú výšku, takže sú zhodné. To znamená, že majú rovnaký obsah a dĺžky strán:
S_{PQX} = S_{DCX} = 1
Teraz už vieme aj obsahy všetkých trojuholníkov v lichobežníku a ich sčítaním vieme vypočítať obsah.
S = 4+1+1+1+1+2 = 10
Odpoveď: Obsah celého lichobežníka ABCD je teda 10.