Anketa - Ahoj Rieškar, stalo sa ti niekedy, že si nerozumel zadaniam? Chcel by si v lete prísť na denný tábor? Sú nejaké akcie, ktoré by si chcel, aby sme robili častejšie? … Prejsť na článok
×6. príklad - Vzorové riešenie
Zadanie
Stíhačka letí stále rovnakou rýchlosťou. V momente, keď jej špička prejde okolo Merlina s Mackerom, Merlin začne kráčať stále rovnakou rýchlosťou v smere, ktorým letí stíhačka, a Macker sa rovnakou rýchlosťou vydá opačným smerom. Každý zastaví v tom momente, keď okolo neho prejde koniec stíhačky. Vieme, že Merlin prešiel 45 metrov a Macker 30 metrov. Aká dlhá je stíhačka?
Vzorové riešenie
Kým koniec stíhačky dobehne Mackera, stihne Macker prejsť 30\,\text{m}. Zo zadania vieme, že Macker a Merlin idú rovnakou rýchlosťou, Merlin teda za ten istý čas prejde tiež 30\,\text{m}. Potom stihne prejsť ešte 15\,\text{m}, kým ho koniec stíhačky dobehne. Koniec stíhačky za ten čas, čo Merlin prejde týchto 15\,\text{m}, prejde 75\,\text{m} (koniec stíhačky išiel od bodu, kde Macker zastavil, do bodu, kde Merlin a Macker začínali, a z tohto bodu ešte 45\,\text{m} k Merlinovi). Stíhačka teda ide 5-krát rýchlejšie (\frac{75\,\text{m}}{15\,\text{m}}=5). Teraz vieme, že od začiatočného bodu Merlin prejde 45\,\text{m}. Vieme, že predok stíhačky prejde 5-krát viac, takže 225\,\text{m}. Koniec stíhačky prešiel od začiatku do bodu, kedy zastavil Merlina 45\,\text{m}. Stíhačka má teda (225\,\text{m}-45\,\text{m}) 180 metrov.
Iné riešenie
Tento príklad sa dá vypočítať aj vďaka vzorcu v=\frac{s}{t}, kde v je rýchlosť, s je prejdená vzdialenosť a t je čas. Určíme si, že v_s bude rýchlosť stíhačky, v_m rýchlosť Merlina a Mackera, a dĺžka stíhačky bude d.
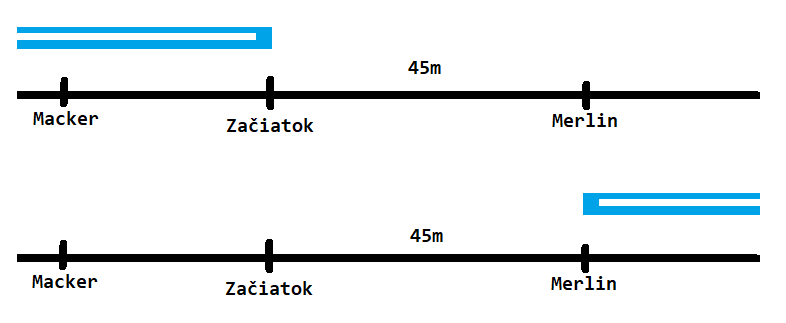
Za nejaký čas prejde Merlin 45\,\text{m} (t=\frac{45\,\text{m}}{v_m}). Za ten istý čas stíhačka prejde svoju dĺžku a navyše ešte 45\,\text{m} (t=\tfrac{(45\,\text{m}+d)}{v_s}). Vznikli nám dve rovnice, ktoré vieme dať do rovnosti.
\dfrac{45\,\text{m}}{v_m}=\dfrac{(d+45\,\text{m})}{v_s}\\ \dfrac{v_s}{v_m}=\dfrac{(d+45\,\text{m})}{45\,\text{m}}
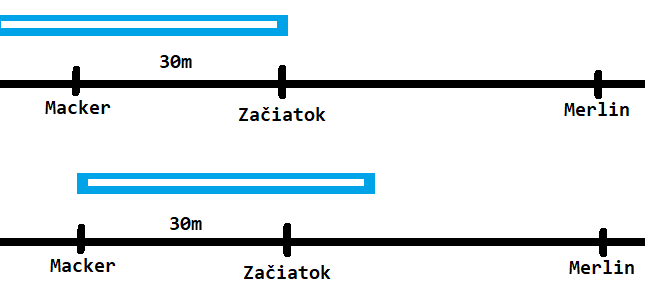
Za nejaký iný čas prejde Macker 30\,\text{m} (t'=\frac{30}{v_m}). Za tento čas prejde stíhačka svoju dĺžku bez 30\,\text{m}, ktoré išiel Macker naproti (t'=\tfrac{(d-30\,\text{m})}{v_s}).
\dfrac{30\,\text{m}}{v_m}=\dfrac{(d-30)}{v_s}\\ \dfrac{v_s}{v_m}=\dfrac{(d-30\,\text{m})}{30\,\text{m}}
Vzťahy pre \frac{v_s}{v_m} si vieme dať do rovnosti a zistíme dĺžku stíhačky d.
\dfrac{(d+45\,\text{m})}{45\,\text{m}}=\dfrac{(d-30\,\text{m})}{30\,\text{m}}\\ 30(d+45\,\text{m}) = 45(d-30\,\text{m})\\ 30d+1350\,\text{m} = 45d-1350\,\text{m}\\ 2700\,\text{m} = 15d\\ 180\,\text{m} = d
Odpoveď: Stíhačka je dlhá 180\,\text{m}.