6. príklad - Vzorové riešenie

Označme si číslo, ktoré si Karin napíše na papier x, potom aj počet posebeidúcich čísel je x. Rozdeľme to teraz na dva prípady, ak x, je nepárne, tak určite existuje v danej postupnosti postupne o jedna sa zväčšujúcich čísel dáke stredné číslo. Toto číslo si pomenujme y. Potom naša postupnosť vyzerá, pre prípad x=5 takto:

y-2;\, y-1;\, y;\, y+1;\, y+2

Už na tomto malom prípade si môžeme všimnúť, že nám tie zvyšky do seba tak pekne zapadajú, somozrejme by sme to chceli zovšeobecniť. Takže od toho stredného čísla, ktoré vždy existuje, nám čísla jedným smerom rastú a druhým smerom klesajú, s tým, že dokopy ich je x, preto práve (x-1)\div2, bude väčších ako to stredné, ktoré je y. Takže dostávame:

y-(x-1)\div2;\, \ldots; y-1;\, y;\, y+1;\, \ldots;\, y+(x-1)\div2

Teraz presne to, čo máme navyše v číslach väčších ako y, nám v tých menších chýba. Vo výsledku teda ich súčet môžeme zrátať ako to stredné, y, krát ich počet. Ten je x, súčet vieme teda vypočítať ako x \cdot y. To je očividne delitelné x. Je teda jasné, že ak na papier Karin napíše ľubovoľné, nepárne číslo, x, tak súčet x čísel v rade bude ním delitelný. Toto má aj peknú geometrickú interpretáciu, kde je vidieť, ako sa tie čísla skladajú do seba: 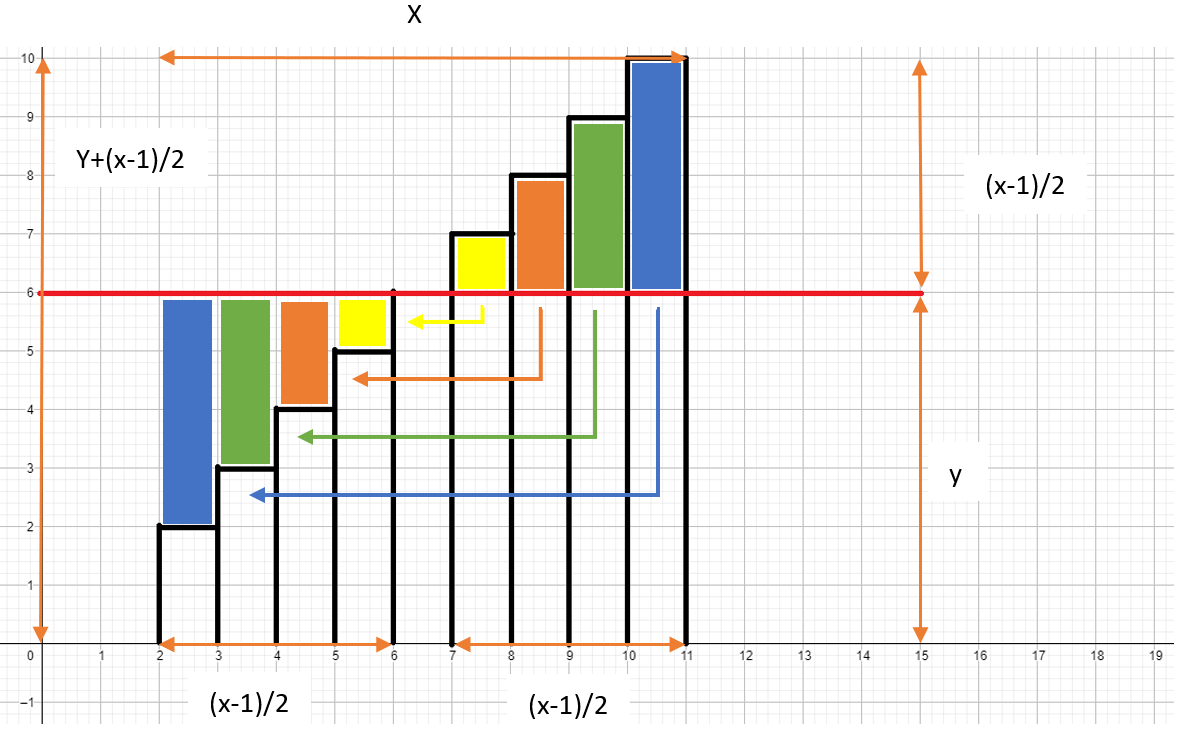Keď chceme tú postupnosť zrátať, tak vlastne môžeme zrátať obsah obdĺžnika s dĺžkami strán x a y.

Pokiaľ Karin na papier napíše párne číslo, tak sa na to vieme pozerať veľmi podobne. Hlavný rozdiel je v tom, že nevieme nájsť toto stredné číslo. Zvoľme si naše nové y, to menšie z dvoch stredných čísel. Naša postupnosť vyzerá potom tak, že každý jej člen, okrem toho najväčšieho má pár, s ktorým dáva súčet y:

y-(x-2)\div2;\, \ldots;\, y-1;\, y;\, y+1;\, \ldots;\, y+(x-2)\div2;\, y+(x-2)\div2+1

Ich súčet vieme vyjadriť ako súčet tých, ktoré do seba po dvoch zapadajú, ktorých je x-1 a k nim prirátame ten posledný člen. Nakoniec celkový súčet bude teda:

(x-1) \cdot y+(y+(x-2)\div2+1)=x \cdot y+x\div2.

Môžeme si všimnúť, že daný súčet teraz nie je deliteľný x, lebo nám ostane y+\frac{1}{2}, čo nie je celé číslo. Preto ak Karin na papier napíše párne číslo x, tak súčet x posebeidúcich čísel nebude deliteľný x. Odporúčam sa aj nad touto druhou časťou zamyslieť aj geometricky.

Komentár: Vo všeobecnosti ste príklad veľmi pekne zvládli. Hlavný problém bol, že mnohí z vás úlohu popísali dosť krátko a často sa nedostatočne venovali dôležitým bodom v riešení.