9. príklad - Vzorové riešenie

Pozrime sa na to, ako bude vyzerať šachovnica na konci hry. Ak by na konci hry boli v nejakom riadku alebo stĺpci iba bezpečné políčka, tak by si ešte daný riadok alebo stĺpec mohla vybrať strana, ktorá je na ťahu. Tým pádom by to nemohol byť koniec hry. Na konci hry teda musí byť v každom riadku a v každom stĺpci na šachovnici aspoň jedno nebezpečné políčko.

Z toho teda vyplýva, že na konci hry existujú aspoň dve nebezpečné políčka, ktoré sú v navzájom rôznom riadku aj stĺpci. Pozrime sa teraz na tieto dve nebezpečné políčka, ktoré si na obrázku označíme čiernou farbou. Ak sa prvé z týchto políčok nachádza v k-tom riadku a x-tom stĺpci, tak sa mohlo zmenšiť len vybratím k-tého riadku alebo x-tého stĺpca. Keďže sa dané políčko zmenšilo o 99, tak súčet počtu vybratí k-tého riadku a počtu vybratí x-tého stĺpca za celú hru musel byť 99. Pozrieme sa teraz na druhé nebezpečné políčko, ktoré je v l-tom riadku a v y-tom stĺpci. Takisto musí platiť, že súčet počtu vybratí l-tého riadku a y-tého stĺpca za celú hru musel byť 99.

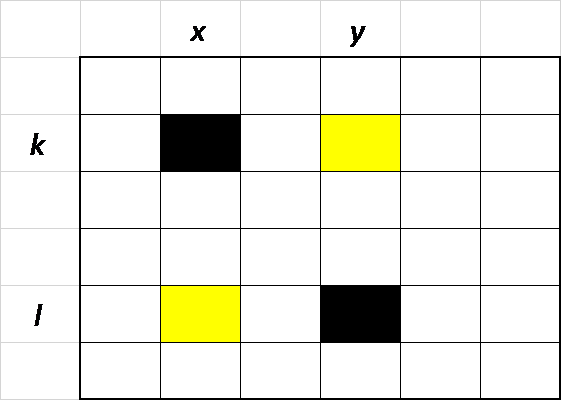
Označme si k_v ako počet vybratí k-tého riadku, l_v ako počet vybratí l-tého riadku, x_v ako počet vybratí x-tého stĺpca a y_v ako počet vybratí y-tého stĺpca. Naše poznatky si vieme zapísať do nasledujúcich dvoch rovníc

Sčítaním rovníc dostaneme

Pozrime sa teraz na žlté políčko v k-tom riadku a y-tom stĺpci. Jeho hodnota sa od začiatku hry zmenšila o súčet počtov vybratí k-tého riadku a y-tého stĺpca. Preto na ňom musí byť na konci hry hodnota

Takisto keď sa pozrieme na žlté políčko v l-tom riadku a v x-tom stĺpci, jeho hodnota musí byť

Z využitím zistených poznatkov vieme, že súčet hodnôt na týchto dvoch žltých políčkach na konci hry je

Keďže žiadne z políčok nemôže nadobúdať zápornú hodnotu, tak obidve políčka musia mať hodnotu 0 na konci hry a byť nebezpečné.

Pozrime sa teraz na hodnotu ľubovoľného políčka na šachovnici na konci hry. Vieme, že na konci hry musí byť v každom riadku a v každom stĺpci aspoň jedno nebezpečné políčko. Keďže v žiadnom riadku ani stĺpci nie sú iba bezpečné políčka, toto ľubovoľné políčko je buď nebezpečné, alebo sa nachádza v riadku s aspoň jedným nebezpečným políčkom a aj v tom istom stĺpci sa nachádza aspoň jedno nebezpečné políčko. Už sme dokázali, že ak sa zároveň nachádza v rovnakom riadku s nebezpečným políčkom aj v rovnakom stĺpci s nebezpečným políčkom, musí byť tiež nebezpečné. Z toho vyplýva. že naše políčko musí byť tiež nebezpečné na konci hry.

Dokázali sme, že ľubovoľné políčko na šachovnici musí byť na konci hry nebezpečné. Tým pádom musia byť na konci hry všetky políčka nebezpečné, teda mať hodnotu 0. Celkovo je na šachovnici n^2 políčok a všetkým sa za celú hru znížila hodnota o 99. Súčet hodnôt políčok na šachovnici sa teda znížil za celú hru o 99n^2. Každým ťahom sa zníži n políčkam hodnota o 1 a teda súčet hodnôt políčok na šachovnici sa zmení o n každým ťahom. Celkový počet ťahov, ktorý sa musel zahrať je

Pretože prehráva strana, ktorá už nemôže zahrať ťah, začínajúca strana vyhrá ak zahrá posledný ťah. To nastáva pokiaľ je počet ťahov za hru nepárny, čo pri počte ťahov 99n nastáva pri nepárnom n. Pri párnom n teda začínajúca strana prehrá, keďže vtedy je celkový počet ťahov párny.

Odpoveď: Začínajúca strana vyhrá pri nepárnom n.