Zadania 1. kola
Kde bolo tam bolo, v krajine za 14\pi sinusoidy, kde harmonické rady divergovali a suma fibonacciho čísel na mínus prvú konvergovala, bol na vrchu jednej skaly raz zakliaty hrad.
1. príklad
Kategórie:
5

Hovorí sa, že na samotnom vrchole hradu žije princezná. Túto princeznú treba samozrejme zachrániť! No to nie je také jednoduché. Hrad má totiž 28 poschodí, ktoré sú plné strašných príšer. Príšer je tak veľa, že ani ich zamestnávateľ si nepamätá, koľko ich je. Snaží sa to síce mať zapísané, no je vcelku náročné v tom nemať chaos.
2. príklad
Kategórie:
5
6
Niet sa ale čoho obávať! Po princeznú prichádza záchrana. Statočný rytier Lychondražej sa rozhodol, že princeznú zachráni, a práve teraz na tom usilovne pracuje. Teda práve teraz nie. Teraz práve padá z osemnásteho poschodia, a popri tom si hovorí: “Osemnáste poschodie! Prečo to musí byť vždy osemnáste poschodie? Cez všetky nižšie poschodia sa dokážem prebojovať takmer bez problémov, tak prečo nie aj cez osemnáste? Keby som mal jeden peniaz za každýkrát, čo som sa dostal až na osemnáste poschodie a spadol z neho, mal by som… Mal by som… Koľko peňazí by som vlastne mal?”
3. príklad
Kategórie:
5
6
7
Kým Lychondražej vypočítal, koľko peňazí by mal, stihol dopadnúť na zem. Postavil sa a vybral sa do obchodu na prízemí. Za peniaze, ktoré v hrade nazbieral, si teraz kúpi nové vybavenie a keď sa potom vydá do hradu znova, pôjde mu to (snáď) lepšie a možno sa konečne dostane cez to osemnáste poschodie. V obchode už na neho čakala predavačka Anna “AnkaP” Peniažková. AnkaP zrovna dokončila svoj najnovší výrobok, ktorý vytvorila z namaľovaných drevených kociek.
4. príklad
Kategórie:
5
6
7
8
AnkaP sa Lychondražejovi prihovorila: “Nebudeš mi veriť, ale teraz tu mám niečo naozaj nesmierne mocné.” Triumfantne zodvihla drevené kocky čerstvo natreté trblietavou farbou k nebu. “Áno, zrak ťa neklame, kamarát! Sú to naozaj legendárne Diamantové Bloky, presne tie isté, aké pred storočiami vyrobil legendárny baník Štefan Ťažremeslo! Legenda hovorí, že pokiaľ nimi hodíš ako hracími kockami dostatočne ďaleko, tak sa možno stane niečo cool, možno nie, neviem, ja som len skromná predavačka. Ako vždy hovorím: Spokojnosť alebo vrátenie peňazí! A keď už sme pri predávaní, určite ti došli elixíry zdravia! Kúp si tucet za dvojnásobnú cenu, a ďalší elixír dostaneš za trojnásobnú!!!”. Lychondražej nebol zase až taký hlúpy, ale AnkaP bola veľmi dobrá predavačka. Otázka nebola, či si to všetko Lychondražej naozaj kúpi, ale koľko na ňom AnkaP zarobí.
5. príklad
Kategórie:
5
6
7
8
9
Nakoniec AnkaP Lychondražejovi predala dvadsaťšesť elixírov zdravia, všetky Diamantové Bloky, pravé originály piatich legendárnych mečov (Excalibur, Durandal, Caledfwlch, Muramasa, a pre istotu ešte jeden Excalibur), zopár ton polorozpusteného cukru (bez akejkoľvek nádoby na ich uskladnenie) a policajnú búdku, ktorá je zvnútra menšia ako zvonka, a dá sa použiť na cestovanie časom do budúcnosti tak, že vnútri počkáš tak dlho, o koľko sa chceš presunúť (možno stojí za to spomenúť aj, že táto búdka je neprenosná, a nemá v sebe zabudovaný spôsob, akým by sa do nej dalo vstúpiť). Keď sa Lychondražej zase raz vybral zachrániť princeznú, AnkaP vytiahla svoj telefón. AnkaP má veľa kontaktov, preto ich má usporiadané zaujímavým spôsobom.
6. príklad
Kategórie:
5
6
7
8
9
Na osemnástom poschodí sa medzitým príšery pripravovali na Lychondražejov opätovný príchod. Doteraz sa im darilo ho zakaždým poraziť a zhodiť späť na zem, ale bolo to čím ďalej, tým ťažšie, pretože Lychondražej sa stával silnejším a silnejším. Každé poschodie má svojho kapitána, ktorý na ňom koordinuje príšery. Toto poschodie mal na starosti Kapitán Stylogroy, a ak sa Lychondražej chce dostať ďalej, musí ho poraziť. Zrovna si nacvičovali s príšerami bojový tanec, keď vtom mu začal zvoniť telefón. Samozrejme, kto iný by mu volal, ako jeho zamestnávateľ? Zdvihol.
“Áno, pani Peniažková?”
“Ako sa vám darí? Je pravda, že Lychondražej má s vami problém?”
“Je to pravda, nejako nedokáže pochopiť, že naše útoky sú vždy podľa tanca, ktorý robíme. Nikdy sa im nevie poriadne vyhnúť. Prečo?”
“Obávam sa, že onedlho začne strácať motiváciu. Mohli by ste mu to žľahčiť, nech si myslí, že sa zlepšuje, respektíve že moje výrobky fungujú?”
“Ako prikazujete, šéfka.”
“Áno, pani Peniažková?”
“Ako sa vám darí? Je pravda, že Lychondražej má s vami problém?”
“Je to pravda, nejako nedokáže pochopiť, že naše útoky sú vždy podľa tanca, ktorý robíme. Nikdy sa im nevie poriadne vyhnúť. Prečo?”
“Obávam sa, že onedlho začne strácať motiváciu. Mohli by ste mu to žľahčiť, nech si myslí, že sa zlepšuje, respektíve že moje výrobky fungujú?”
“Ako prikazujete, šéfka.”
7. príklad
Kategórie:
5
6
7
8
9

Po hovore šla AnkaP upratať cenovky na tovare. Ako vždy plánovala mať všetky ceny nesmierne vysoké, aby sa pri dohadovaní ceny každá rozumná cena zdala hrozne nízka. Aby ale mala lepšiu výhovorku predať zopár výrobkov, rozhodla sa, že im cenu zníži zo strašne nehoráznej na iba celkom nehoráznu, aby sa vedľa ostatných zdali lacnejšie.
8. príklad
Kategórie:
5
6
7
8
9
Začína AnkaP a potom sa s Trhom strieda v ťahoch. Na začiatku je 10 nepoužitých kartičiek s ciframi od 0 po 9, každá práve jedna. Hráč, ktorý je na ťahu vezme ľubovoľnú nepoužitú kartičku a uloží ju za ostatné použité kartičky doprava. Musí platiť, že po n-tom ťahu, je n-ciferné číslo tvorené použitými kartičkami deliteľné n. Prehrá hráč, ktorý už nemôže spraviť žiaden ťah. Kto má víťaznú stratégiu? Víťazná stratégia znamená, že hráč vie voliť také ťahy, aby vyhral bez ohľadu na to, aké ťahy vykonáva jeho súper.
Keď AnkaP doupravovala ceny, išla čakať pred hrad. Netrvalo dlho a z neba spadlo niekoľko drevených kociek pomaľovaných trblietavou farbou, akoby ich niekto hodil najsilnejšie, ako len môže, z približne desiateho poschodia. AnkaP kocky pozbierala, aby z nich spravila niečo, čo môže predať a z čoho nebude poznať, že sú to tie isté kocky, ktoré Lychondražejovi už raz predala. Rozhodla sa preto, že z nich niečo vyreže.
9. príklad
Kategórie:
5
6
7
8
9
Po rozrezaní boli síce kúsky dreva plné trčiacich triesok, ale to nevadilo, pretože AnkaP mala veľa lepkavých obalov od cukríkov a ešte viac bielidla. Vybielené obaly od cukríkov vyzerajú úplne ako leukoplasty, ktoré môže Lychondražejovi predať na jeho triesky. Ale zase nie sú príliš lepkavé, teda mu budú padať a bude si musieť kupovať ďalšie. Potrebovala už len odporúčanie od deviatich z desiatich lekárov, aby Lychondražej uveril, že leukoplast naozaj funguje. Získa ho pochybnými asociáciami, nasledovanými matematickými úlohami, ktoré lekára zmätú, napríklad takto: Funguje tento leukoplast? Samozrejme, má všetky tieto úžasné funkcie!
10. príklad
Kategórie:
5
6
7
8
9
AnkaP konečne zmiatla deviateho lekára dostatočne na to, aby jej dal svoje odporúčanie. Bolo to práve včas, pretože Lychondražej už bol na ceste späť (vo voľnom páde). Tentokrát sa nedostal ani na to nenávidené osemnáste poschodie, spadol už z pätnásteho, pretože si zabudol priniesť teplé oblečenie. Napriek tomu, že sa mu občas podarilo takto ľahko sa nechať zhodiť, v jeho mozgu sa postupne zosilňovali určité spojenia, takže bol v prebojovávaní sa hradom čím ďalej tým lepší.
Prémia 1
Kategórie:
5
6
7
8
9
Tento príklad je iný, ako ostatné. Nemusíš spisovať svoj postup, stačí nám poslať riešenie. Viac informácií nájdeš v pravidlách.
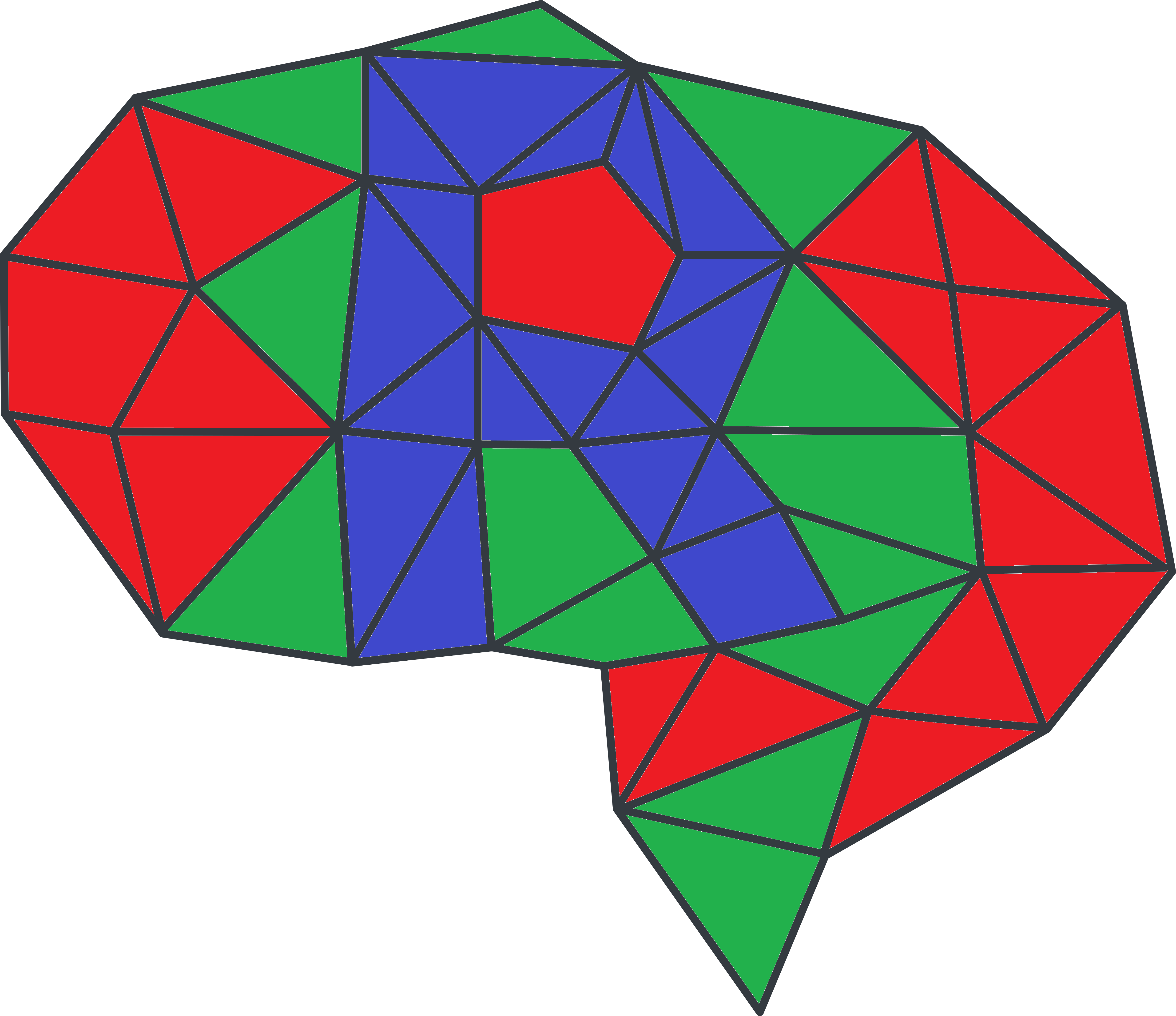
Lychondražejov mozog vyzerá takto:

Obvod takejto oblasti je uzavretá lomená čiara, ktorá zvonka ohraničuje danú oblasť, pričom sa nikdy nedotýka sama seba (teda akékoľvek “diery” vnútri oblasti neovplyvňujú jej obvod). Vašou úlohou je zafarbiť každé políčko jednou z troch farieb tak, aby bol súčet nasledujúcich troch dĺžok čo najväčší:
- Najdlhší obvod oblasti, ktorá je zložená iba z políčok červenej a modrej farby.
- Najdlhší obvod oblasti, ktorá je zložená iba z políčok modrej a zelenej farby.
- Najdlhší obvod oblasti, ktorá je zložená iba z políčok zelenej a červenej farby.
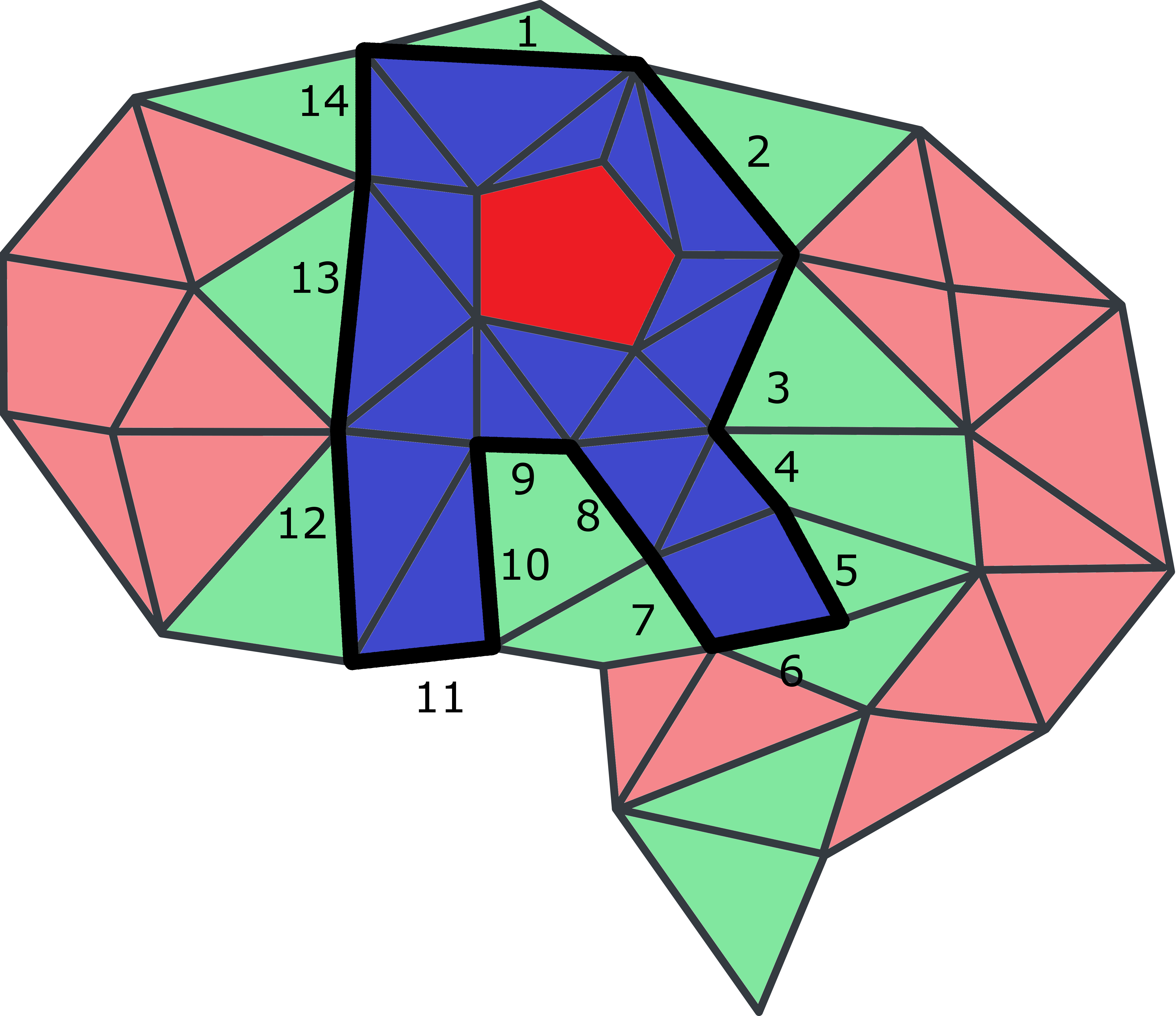
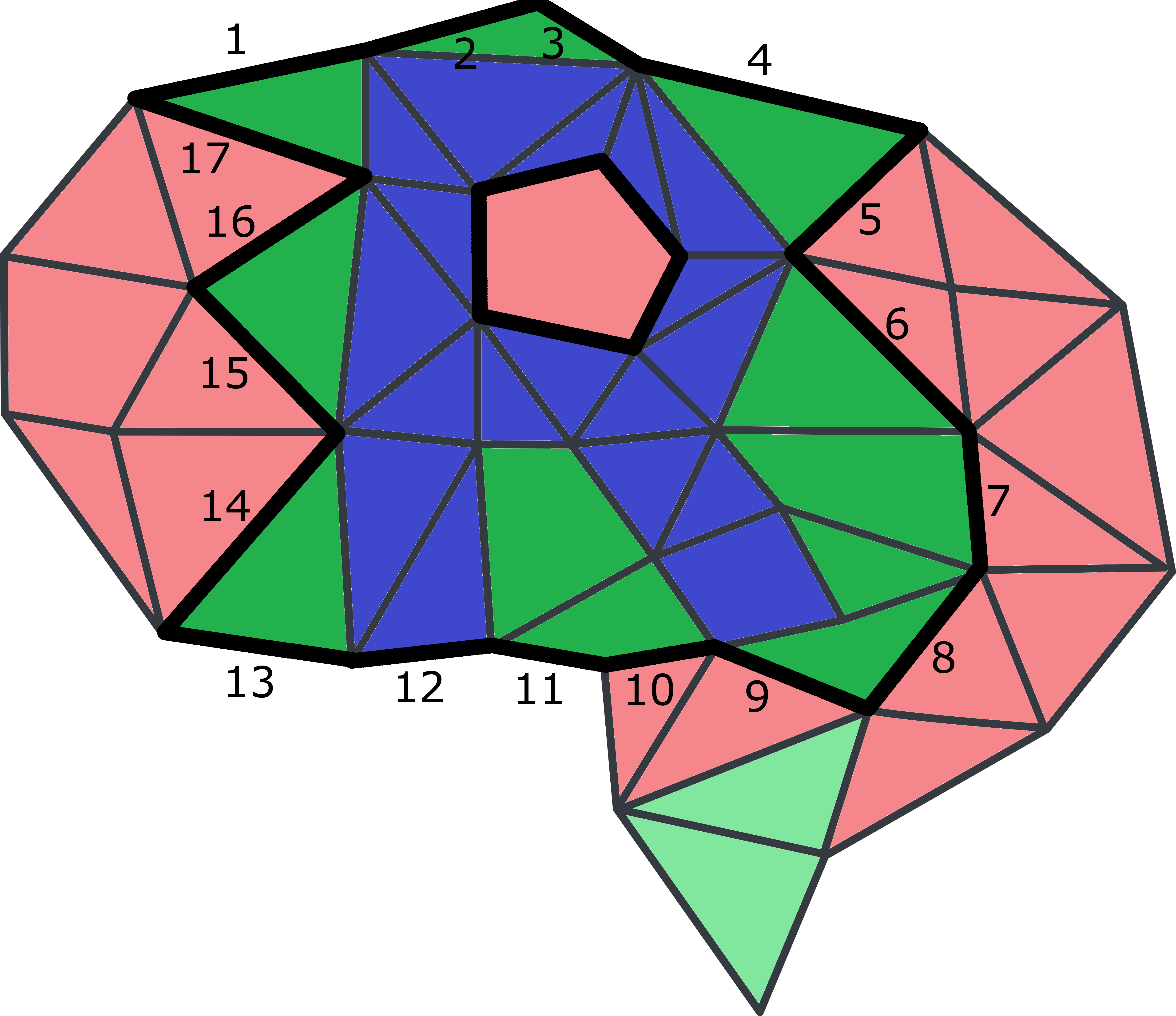
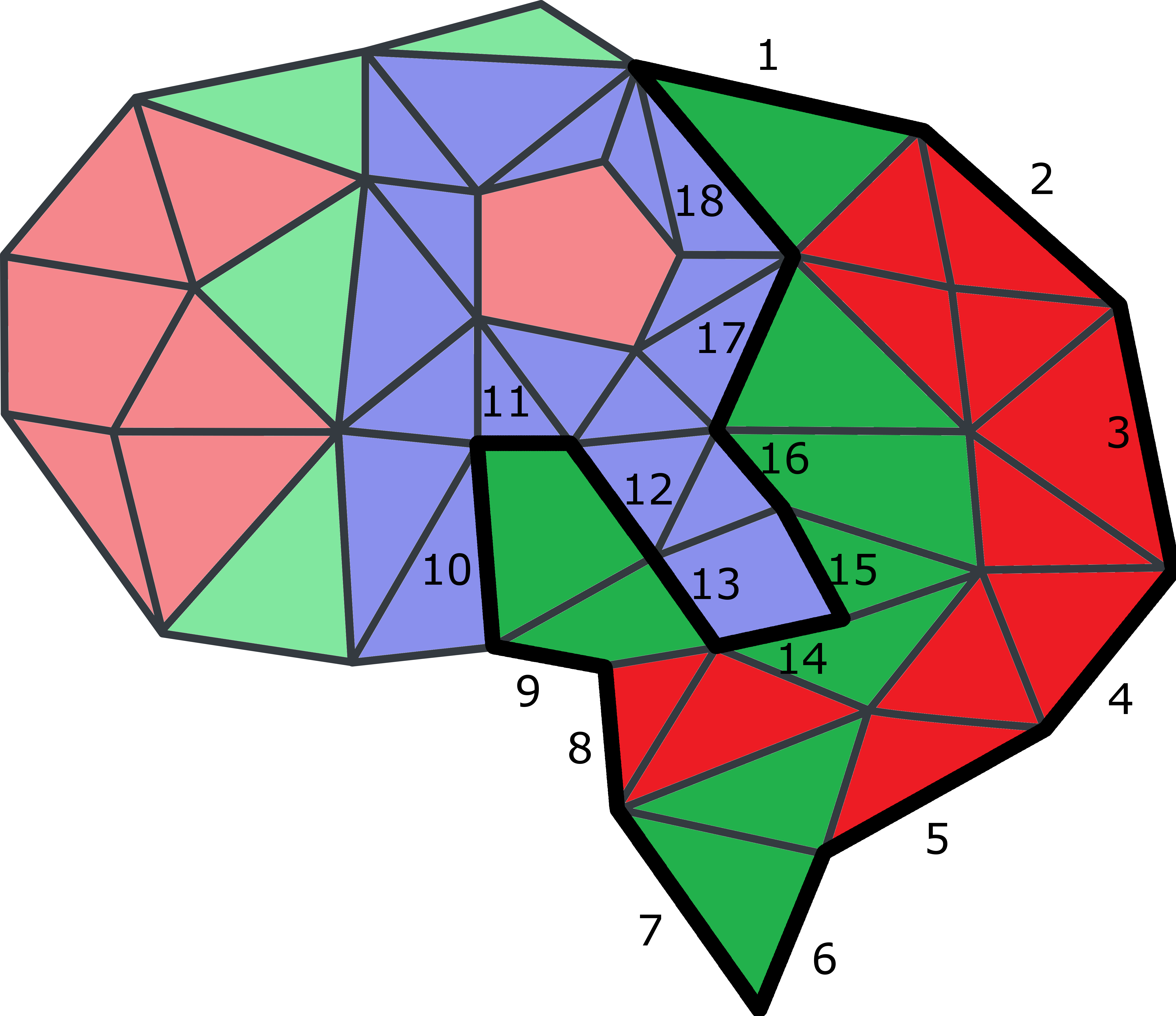
Príklad
Ak by sme mozog ofarbili takto: