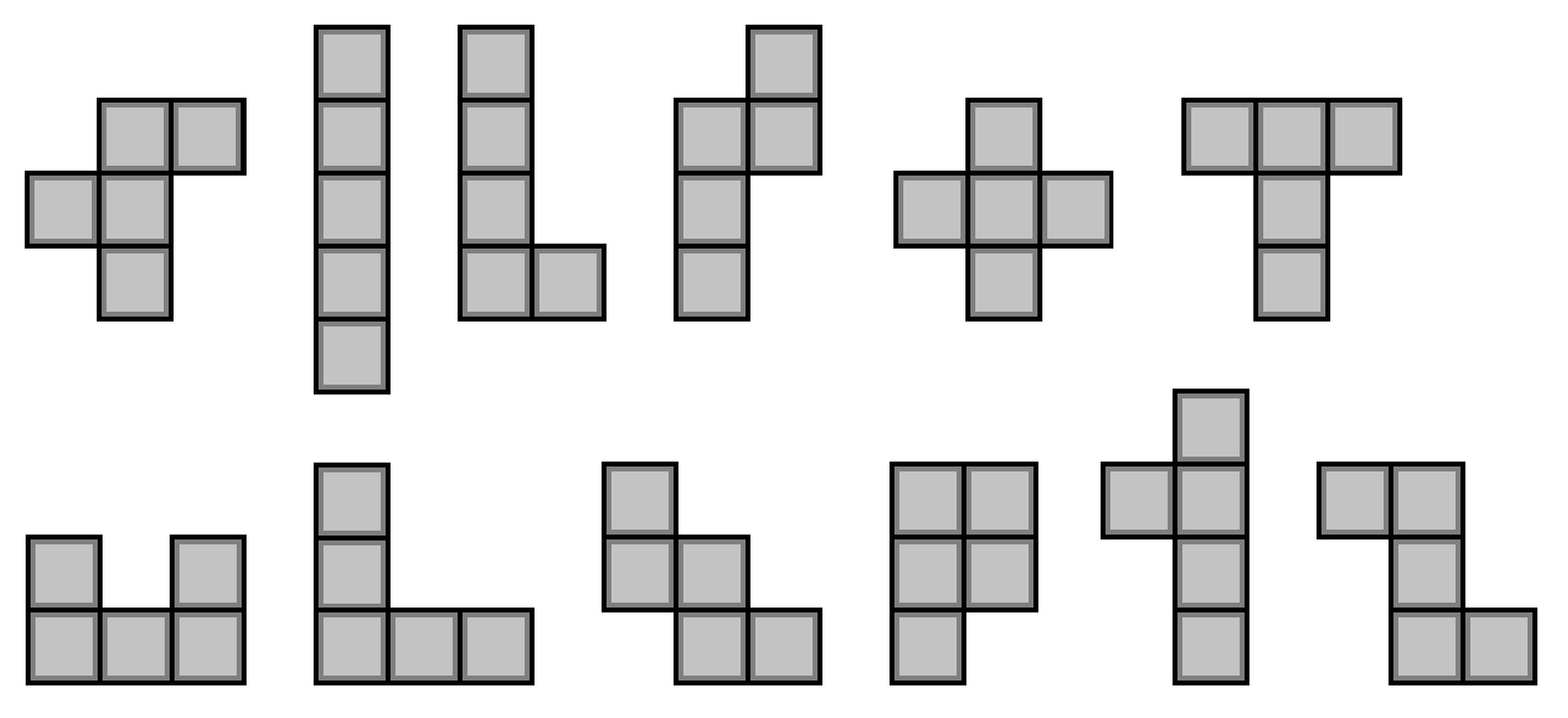Zadania 2. kola

Miška mama nepustila na výlet, lebo musí počítať príklady. Každý deň po škole vypočíta tri príklady. Cez víkend mu jeho brat Maťko poradí, teda Miško zvládne vypočítať až päť príkladov za deň. Po niekoľkých dňoch sa zamyslel, že ani nevie kedy s počítaním príkladov začal. Našťastie príklady boli očíslované a posledný, čo vypočítal mal číslo 111. Ktorý deň v týždni začal? Nájdite všetky možnosti.

Repa sa moc vyzná do digitálnych technológii a už zabudol, že existujú aj ručičkové hodiny. Aby toho nebolo málo, hodinky, čo doma našiel, majú všetky ručičky rovnako dlhé a nemajú čísla. Preto nevie, ktorá ručička, čo znamená a ani ktoré číslo má byť hore. Vedeli by ste mu poradiť, koľko môže byť hodín, ak viete o ručičkových hodinách toľko koľko Repa a hodiny ukazujú to, čo na obrázku?

Tony sa chcel naobedovať a tak si na trhu kúpil sto vecí dokopy za sto dukátov. Šálka stojí \frac{7}{2} dukátu, Repa stojí \frac{4}{3} dukátu a Šošovička stojí \frac{1}{2} dukátu. Koľko čoho si Tony na trhu kúpil?

Imro je velký matik, preto má jeho hlava tvar štvoruholníka ABCD. O jeho hlave platí, že strana AB je rovnobežná so stranou CD, pri vrchole B je pravý uhol, trojuholník ADB je rovnoramenný so základňou AB a strany BC a CD sú obe dlhé 10 cm.
Zistite obsah Imrovej hlavy (štvoruholníka ABCD).

Šošo a Adam sa chceli ísť hrať šach, no zistili,že Adam stratil všetky figúrky okrem jednej veže. Zahrali sa teda inú hru. Vežu postavili do pravého horného rohu šachovnice s rozmermi 8\times 8, a mohla sa pohybovať iba doľava a dole o ľubovoľný počet políčok. Kto vyhrá (a ako to spraví), ak začína Adam a

1. ten, ktorý už nemôže spraviť ťah prehrá?
2. ten, ktorý už nemôže spraviť ťah vyhrá?

Ema s Terkou piekli koláč. Keď upiekli koláč kosodĺžnikového tvaru, chceli ho aj farebne vyzdobiť. Zvolili si bod niekde v koláči a spojili ho s vrcholmi. Vzniknuté časti vyzdobili marcipánom. Použili na to 5 balení modrého marcipánu, 8 balení žltého a 6 balení zeleného marcipánu. Koľko balení červeného marcipánu majú kúpiť, aby im žiaden neostal, ani nechýbal? V obrázku sú vyznačené obsahy daných častí koláča. Časť s červeným marcipánom je označená otáznikom.

Lístky na Merlinovu kúzelnícku show stáli nejaký celočíselný počet dukátov, väčší ako 1. Navyše platilo, že súčet ceny detskej a dospeláckej vstupenky, rovnako ako ich súčin, bol mocninou prvočísla. Nájdite všetky možné ceny vstupeniek.

Ela s Miškom sa pohádali, a teraz sa nechcú vidieť. Miško sa ale chce dostať za Maťkom, aby sa z toho vyrátal. Problém však je, že cestou môže stretnúť Elu. Chce ísť čo najrýchlejšie preto chodí iba dole a doprava. Aká je šanca, že ju stretne, ak

1. si vopred vyberie jednu z možných ciest a tej sa bude držať,
2. na každej križovatke, kde má voľbu dvoch možností, si vyberie jednu s rovnakou pravdepodobnosťou ako druhú?

Maxo má svoj štýl a preto nosí okuliare v tvare pravouhlého trojuholníka, ktorého odvesna má dĺžku 40 milimetrov. Všimol si, že keď sa pozrie iba jedným okom, tak Slnko je vlastne kružnica vpísaná do sklíčka jeho okuliarov. Z tohto pohľadu je Slnko kruh s polomerom 15 milimetrov. Aký obsah má jedno jeho sklíčko na okuliaroch?

Havoš má veľmi rád čokoládu. Doktor mu ale povedal, že má alergiu na mlieko, či čo to, a že by mal prestať jesť toľko čokolády. Havoš odvtedy nikdy nezjedol celú čokoládu, ale vždy si nechal kúsok tvorený práve piatimi dielikmi. Teraz ich už má všetkých dvanásť rôznych, tak sa s nimi začal hrať. Má štvorčekovú mriežku 42\times42 štvorčekov a 12 dielikov pentomín (viď obrázok). Pentominá chce vložiť do mriežky tak, aby ohraničili, čo najviac políčok. Ohraničené políčka môžu susediť stranou alebo rohom jedine s iným ohraničeným políčkom, alebo políčkom prekrytým niektorým pentominom. Dieliky môže ľubovoľne otáčať alebo preklopiť, nemôže však použiť ten istý viackrát. Pomôžte Havošovi nájsť také rozloženie pentomín, ktoré ohraničí čo najväčší počet políčok.