Zadania 3. kola
“Čo sa deje?” zvolal vystrašený Lukáš.
Klopanie neprestávalo. Boli na dne mora, nečakali, že sa tu bude vyskytovať akýkoľvek život alebo civilizácia.
“Netuším…” zneistene vyhlásil Alex.
Vtom klopkanie ustalo, a po chvíli napätého ticha chlapci skoro dostali infarkt, keď krabica začala opäť klesať.
“AKO EŠTE HLBOKO???”
“NEVIEM. Pozri hĺbkomer.”
“Nevyzerá že by dobre fungoval, budeme musieť počkať, kým sa mu zachce hovoriť správne hodnoty”
“Ale veď to môže trvať celé dni!”
1. príklad
Krabica počas každého pracovného dňa klesne o 1000 metrov hlbšie. Cez víkend stojí na mieste. Alex sa na konci každého z troch po sebe idúcich dní opýtal hĺbkomeru: “Koľko metrov sme už tento týždeň klesli?”. Hĺbkomer podal tieto informácie:
- Prvý deň: Klesli sme 67 metrov
- Druhý deň: Klesli sme 3000 metrov
- Tretí deň: Klesli sme viac ako 2000 metrov
Hĺbkomer však správne funguje iba tie dni, kedy krabica neklesá. Inak určite povie nesprávny údaj.
Ktorý deň v týždni mohol byť prvý z tých, kedy sa alex pýtal hĺbkomeru? Nájdite všetky možnosti.
Buch. Krabica opäť doľahla na dno.
“V tekejto hĺbke fakt nechcem počuť klopkanie.”, vyhlásil Lukáš, a vtom sa klopkanie vrátilo znova. Tentokrát však znelo trochu naliehavejšie, a hýbalo sa po obvode krabice. Alex sa zamračil. Klopkanie sa zastavilo na jednom mieste a začalo byť rapídnejšie. Keď sa Alex zadívaj pozornejšie, zazrel obrys akéhosi panelu, ktorý si doteraz nevšimol, a keď ho odklopil, čakalo chlapcov ďalšie prekvapenie.
“Haló? Počuť ma?”
“Áno?” odpovedal zmätený Alex, ktorý pod panelom zízal na tlačidlá a komunikátor.
“Výborne. Sme záchranný tím pre vydedencov z Esarp. Náš tím v metropole kóduje do krabíc tajné gombíky, aby sa dalo vydedencov zachrániť. Sú tu však bezpečnostné protokoly. Máte tam nejaké informácie?”
2. príklad
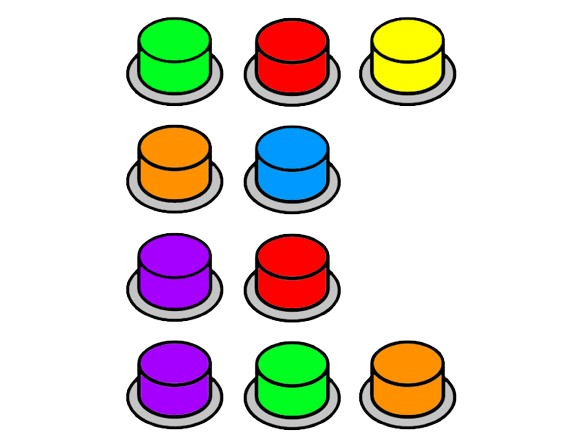
Na obrázku je znázornených 10 gombíkov, z ktorých práve jeden je záchranný. Lukáš iba vie, v ktorom riadku sa gombík nachádza, a Alex pozná jeho farbu ale nič iné.
Alex povedal: Neviem, ktorý gombík je záchranný.
Na to sa ozval Lukáš a hovorí: Nevedel som, ktorý gombík je záchranný, ale po tom, čo sa ozval Alex, to už viem.
Zistite aj vy, ktorý gombík je záchranný.
Keď Lukáš stlačil správny gombík, ozval sa rachot. Steny kocky sa s rachotom uvoľnili a dnu sa naliala voda, chlapcov pretočilo a ledva sa dokázali nadýchnuť. Lukáš nič nevidel, ale cítil, ako ho akési ruky silne uchmatli a ťahali von z kusov železa, až kým ho po chvíli konečne vyhodili na suchú zem. Otvoril oči. Zaslepovalo ho silné svetlo reflektorov, takže videl iba siluety ľudí v skafandroch a Alexovu postavu.
“Dobrá práca” ozývalo sa pochvalne zo všetkých strán, a kým si ľudia vyzliekali skafandre, k Lukášovi pristúpil akýsi muž, ktorý si ho nevrlo prezeral.
„Jak sa voláš“ vybafol naňho.
„Lukáš, a toto je Alex.“
„Ja som tu kapitán, takže počúvate mňa. Takých ako vás vyťahujeme každú chvíľu, takže budťe radi že tu sme. Makajte za ním,“ mávol kapitán rukou na vysokého muža pri chlapcoch, a začal nezaujato odchádzať.
„Ja som Mišo. Touto obdĺžnikovou chodbou prosím.“
„NIE JE TO OBDĹŽNIK“ zhúkol naňho kapitán.
3. príklad
Chodba má tvar ktorý skonštruujeme takto. Najprv umiestnime body ABCD tak, aby tvorili obdĺžnik so stranou BC dlhšou ako AB. Potom pridáme bod E tak, aby body BCDE tvorili deltoid. Chodba má tvar ako štvoruholník tvorený bodmi ABDE. Vedúci povedali tieto tvrdenia:
- Mišo: ABDE je obdĺžnik!
- Alex: Nie, nie všetky strany sú rovnobežné, ABDE je rovnoramenný lichobežník!
- Lukáš: Nie, žiadne strany nie sú rovnobežné, ale ABDE má aspoň dve zo svojich strán rovnako dlhé!
- Kapitán: Nie, ABDE je všeobecný štvoruholník s rôznobežnými stranami, ktoré majú všetky rôznu dĺžku.
Rozhodnite, kto z určite nehovorí pravdu, kto určite hovorí pravdu, a kto môže ale nemusí hovoriť pravdu (teda či je ich tvrdenie pravda nikdy, vždy alebo iba niekedy, keď umiestnime body ABCDE podľa podmienok). Ak niekto vždy klame alebo vždy hovorí pravdu, nezabudnite dokázať že to tak naozaj bude pri hociakom rozložení bodov spĺňajúcich zadanie.
Nový spoločník vyzeral prívetivejšie ako kapitán, a tak začal Lukáš vyzvedať.
„Kde to sme?“
„Je to jedna základňa odboja proti svetovej vláde,“ hovoril Mišo, kým ich viedol ošarpanými úrovňami základne, „na tamtom mieste často zhadzuje hlavné mesto vyhnancov, tak tých, ktorí ten zostup prežili verbujeme do odboja. Väčšinou neprotestujú. Základňa je síce tajná, ale ďalej týmto smerom sa nachádza normálne mesto Osam.“ Alex s Lukášom mlčky prikyvovali a obzerali sa okolo seba po základni.
„Ako tu máte vôbec elektrinu?“
„To je jednoduché, proste zachytávame energiu mora a generátory z toho robia prúd. Je ich dokonca toľko, že ak jeden v nejakej sekcii vypadne, vždy ho vedia nahradiť dva záložné.“
„Tak to ich musíte mať celkom veľa.”
4. príklad
Generátory sú označené rôznymi celými číslami (môžu byť aj záporné). Zároveň pre čísla na nich platí, že každé sa dá vyjadriť ako súčet nejakých dvoch iných rôznych celých čísel ktoré sú na generátoroch. Koľko najmenej mohlo byť generátorov?
Po chvíli kráčania prišli až k akejsi miestnosti, kde za prepážkou sedel starý mužík. Zvihol hlavu, keď vstúpili.
„Čo to dneska bude?“ spýtal sa, a otvoril prepážku.
„Vaše veci prosím“ ukázal Mišo na dosku za prepážkou.
„Čo sa ide?“
„Dlžíte nám život. Odteraz vlastníme všetky vaše veci, s ktorými ste prišli. Aby ste sa neozývali, že to je nefér, ich hodnota v peniazoch sa po ich ohodnotení férovo rozdelí.“
„To je nefér, ukradli sme to my...“ ozýval sa Alex, ale Lukáš naňho kývol, nech veci dá na stôl. Starček si ich niekam dozadu zobral, ale po netrvalo dlho a bol s vrečúškom vecí naspäť.
„KDE STE TO VZALI?“ otázal sa a otočil sa na Miša, „okolo 3,3 miliónov Bontov.“
Mišovi sa zalesklo v očiach a podal chlapcom akési zariadenie. Ide sa hlasovať o deľbe peňazí.
5. príklad
Majme 101 pirátov, z toho jeden je kapitán. Na začiatku platí prerozdelenie, kde každý má 1 mincu. V každom kroku kapitán navrhne ľubovoľné nové prerozdelenie 101 mincí medzi pirátov. Potom každý pirát okrem kapitána zahlasuje:
- “áno” ak sa mu zvýšil počet mincí oproti teraz platnému prerozdeleniu
- “nie” ak sa mu zníži počet mincí oproti teraz platnému prerozdeleniu
- a zdrží sa hlasovania, ak sa mu počet mincí nezmenil.
Pokiaľ viac pirátov hlasovalo “áno” ako “nie”, navrhované prerozdelenie sa stane platným, inak ostáva v platnosti staré. Nasleduje ďalší krok, a kapitán takto navrhuje prerozdelenia pokým chce. Koľko najviac mincí môže získať kapitán pre seba? Ukážte, ako to môže spraviť, a dokážte, že viac získať nemôže.
„To je absurdné!“ ohradil sa Alex, „však sme dostali strašne málo peňazí!“
Mišo pokrčil plecami. „Smola. Takto to proste funguje. Pravidlá určuje kapitán.“
Vtom Mišovi zabzučal akýsi prístroj pripevenený o jeho helmu.
„Áno? Jasné. Hneď som tam.“ Mišo sa otočil na starkého a niečo mu naznačil rukou. „Počkajte tu,“ povedal chlapcom a vyšiel von z miestnosti. Starký začal odchádzať s vreckom kamsi dozadu, Lukáš ho však zastavil.
„Počkajte!“
Starký sa naňho podozrievavo zamračil.
„Ja som veľký fanúšik technológií, mohli by ste mi prosím vysvetliť, prečo sú tie veci tak vzácne? Veľmi ma to zaujíma.“
Starkému z tváre ihneď zmizol podozrievavý výraz a rozžiarili sa mu oči.
„Je to úplne kúzelná technológia, napríklad takýto veľký Ikrist je skoro nemožné zložiť.“
6. príklad
Nájdite najväčšie párne prirodzené číslo, ktoré sa nedá zapísať ako súčet dvoch nepárnych zložených čísel.
Lukáš sledoval Alexa, ako sa starkého vypytuje na všemožné súčiastky, ktoré ani sám nevedel pomenovať. Nevedel, o čo sa Alex snaží, ale nechcel mu nič kaziť, a tak len mlčky čakal, kým starček nadšene vykladal o niečom, do čoho sa Alex ani Lukáš ani trocha nerozumeli.
„No a toto mladý muž, je niečo, čo by som nikdy neveril že uvidím na vlastné oči,“ hovoril starček, kým vyťahoval akúsú kruhovú súčiastku veľkosti oka, „je to kronový reaktor, ale pozor aký malý! Normálne sú veľké ako táto miestnosť. Tu sa im podarilo spraviť konfiguráciu s naozaj nízkym počtom krónov.“
„Môžem sa pozrieť po lupou? Nevidím.“ pýtal sa Alex.
„Áno áno, aj ja som to ledva videl,“ vravel starček podávajúc lupu Alexovi.
7. príklad
Starček má 2n kronov s číslami od 1 až po 2n. Usporiadal ich do kruhu v nejakom poradí. Z nich potom povytváral všetky možné súčty tak, že vždy sčítal dohromady nejakých n susedných čísel (dohromady teda vytvoril 2n súčtov).
Pre každé n určte, koľko najmenej rôznych súčtov mohol takto dostať, ak usporiadal čísla do kruhu optimálne.
Príklad: ak by sa n rovnalo 3, starček by mohol vytvoriť kruh 5, 3, 4, 6, 1, 2, (znova 5)... a súčty by boli:
- 5+3+4=12
- 3+4+6=13
- 4+6+1=11
- 6+1+2=9
- 1+2+5=8
- 2+5+3=10
Alex sa ešte chvíľu vypytoval, ale potom sa slušne starkému poďakoval. Ten vzal vrecko, z ktorého doteraz vyberal rôzne súčiastky, natešene poprial Alexovi výbornú elektrotechnickú kariéru a stratil sa niekde vzadu. Alex v momente zmenil výraz.
„Skoro som zaspal. Padáme. Cestou sem som videl chodbu označenú ako vchod do mesta.“
Lukáš sa ani nepýtal a nasledoval Alexa, ktorý vybehol z miestnosti von. Prestali bežať, až keď sa nachádzali v tmavej chodbe, ktorá bola označená ako východ do mesta Osam.
„To bol ale hlupák“ vyfúkol Alex.
„Čo si spravil?“
„Vybavil nám lístok domov“ zaškeril sa Alex a ukázal na prsteň.
„TY SI MU TO VYMENIL?“
„A nielen to“ uchechtol sa Alex, „pozri.“
Lukáš len udivene pozeral na Alexa, ako z vreciek vyberá súčiastky.
„Ten starý nevidel ani na vlastný nos, do toho jeho vrecka som mu nasypal kúsky kovu. Ale vymenil som len také súčiastky, na ktorých ťažko vidieť rozdiel. Čo myslíš, za koľko to v súčte predáme?“
8. príklad
Majme niekoľko rôznych kladných celých čísel so súčtom 2025. Aký najväčší môže byť ich súčin?
O peniazoch, ktoré dostali za súčiastky si ani jeden nikdy nedovolil snívať, avšak chlapcov stále trápilo, ako sa z mesta, kde budú za chvíľu hľadanými, dostať.
„Myslíš, že majú ako u nás doma aerobusy, ale tu chodia medzi mestami pod vodou?“
„Netuším,“ odvetil Alex, „mal som však taký nápad. Keď sme už tu a máme peniaze, čo tak byť voľný v pravom slova zmysle?“
Lukáš pochopil. Alex chcel, aby si kúpili svoju vlastnú ponorku.
„Poďme sa pozrieť, či tu vôbec majú nejaké na výber.“
A naozaj, v lokálnom podvodnom prístave bolo na predaj hneď niekoľko hlbokomorských plavidiel, ktoré mali rôzne veľké poklopy.
9. príklad
Ponorka má tvar pravouhlého trojuholníka ABC, v ktorom |AB|=|AC|=1. Bod D leží niekde na úsečke AB. Bod E je priesečník strany BC s osou strany CD. Nájdite najväčšiu a najmenšiu možnú dĺžku úsečky CE.
Kým Lukášovi predajca ukazoval všetky funkcie ponorky, Lukáš ho poriadne ani nepočúval. Bol udivený, ako taká vzducholoď a ponorka toho majú vlastne naozaj veľa spoločného, teda až na to, že mu pri kormidlovaní nevial vietor vo vlasoch. Nevedel, prečo si vlastne vypýtal prehliadku ponorky. Rozhodnotý už bol predtým. Po prehliadke len potichu kývol predajcovi „berieme ju.“
Po tom, čo predajcovi zaplatili dostali papierik s prístupovým kódom a dozvedeli sa meno ich novej ponorky. „Kyklops“. Lukáš sa cítil veľmi napäto, keď pristúpil k systémovej doske a rozšifrovával štyri číselné kódy z papieriku, ktorý im predavač dal.
10. príklad
Máme štyri kladné čísla a,b,c a n. Platia pre ne nasledujúce rovnice:
b = \text{nsd}(c,a) + n
c = \text{nsd}(a,b) + n
Kde \text{nsd}(x, y) značí najväčšieho spoločného deliteľa čísel x, y. Nájdite všetky možné štvorice a,b,c,n.
Najprv sa nič nedialo.
„Kam sa poplavíme najprv?“ spýtal sa Alex Lukáša.
„Pôjdeme niekam, kde sme ešte neboli. Zistíme, aké majú dobrodružstvá tu v Medzizemi.“
Potom sa rozsvietili všetky displeje na palubnej doske, zažli sa svetlá, a ozval sa robotický hlas v cudzom jazyku: „Welcome aboard captian. All systems online.“ Lukáš sa usmial.